介電彈性體驅動單元的動態特性分析

，，

(海軍工程大學 振動與噪聲研究所，船舶振動噪聲重點實驗室，湖北 武漢 430033)

1 引 言

介電彈性體(DE)是指在外加電場載荷激勵下能夠產生較大變形的電活性聚合物(EAP)材料，是一種具有巨大發展潛力的新型智能材料。介電彈性體驅動單元是構成介電彈性體驅動器的基本元件，由柔性電極—材料薄膜—柔性電極組成典型的“三明治”式結構，當在兩個電極之間施加高電壓時，其產生的Maxwell應力將使其間的介電彈性體膜變薄，面積增大；撤去電壓，介電彈性體膜則恢復到原來的形狀。同傳統的驅動器相比，介電彈性體驅動器(DEA)具有變形大、響應速度快、機電轉換效率高、質量輕、低噪聲等獨特優勢[1-2]，近年來在仿生機器人設計、結構振動與噪聲控制等領域受到國內外學者和研究機構的廣泛關注。

目前，國內外的相關研究主要針對介電彈性體材料的準靜態變形特性，有關介電彈性體驅動單元在特定頻率范圍內動態特性的研究則比較有限，主要集中在驅動單元的動態建模仿真和基礎試驗測試等方面。Dubois[3]等人采用瑞利-里茲方法建立了基于有機硅的介電彈性體材料驅動模型，通過控制電壓使系統的共振頻率降低了77%；Suo[4-5]等人先后對預拉伸的球形和圓形介電彈性體薄膜進行了建模仿真，重點研究了系統的非線性振動和共振現象；Goulbourne[6]等人在準靜態模型分析的基礎上，通過試驗研究了變化電壓和機械載荷條件下介電彈性體驅動單元的動態響應；Xu[7]等人利用歐拉-拉格朗日方程推導了介電彈性體驅動單元的動力學模型，分析了系統的動態響應及阻尼因素的影響。本文以介電彈性體驅動器的基本驅動單元為研究對象，重點考慮材料非線性、介電常數變化和慣性效應等因素的影響，從熱力學能量轉化的角度得到了基于Ogden應變能函數的介電彈性體驅動單元的二階常微分運動方程并對其進行了數值分析，得到了系統在恒定和簡諧電場強度情況下的動態響應。

2 介電彈性體驅動單元的運動方程

根據連續介質力學理論，假設施加電壓前介電彈性體驅動單元的尺寸為2L×2L×2H，材料坐標(X,Y,Z)表示驅動單元上任意點的位置，空間坐標(x,y,z)表示空間中任意點的位置，兩坐標原點在驅動單元的中心點處重合，且模型的三個中間主平面X=0，Y=0，Z=0不產生法向位移，見圖1(a)。

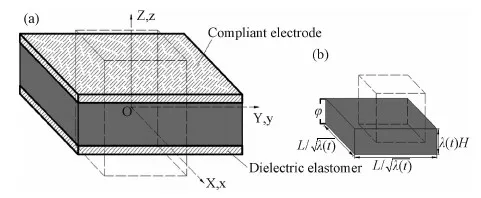
圖1 介電彈性體驅動單元的簡化模型及其坐標Fig.1 Simplified model and coordinate of DE actuating unit

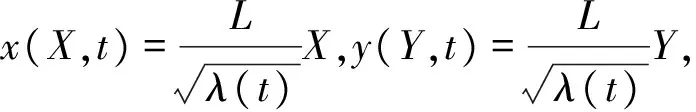
(1)

根據熱力學能量理論，介電彈性體驅動單元亥姆霍茲自由能的變化等于系統的電場能變化和慣性力做功之和，即：

VδF=φδQ+δK

(2)

式中：F為單位體積的亥姆霍茲自由能，V=HL2為材料的體積，整個系統亥姆霍茲自由能的變化可以表示為VδF；φδQ為系統電勢變化所做的功，其中φ和Q分別為電勢和電荷量；δK為系統中慣性力所做的功。

對于存在機電耦合的介電彈性體驅動單元，其亥姆霍茲自由能由彈性能和靜電能兩部分組成[8]。本文采用一階Ogden應變能函數來計算驅動單元的彈性能，則系統單位體積的亥姆霍茲自由能為：

(3)

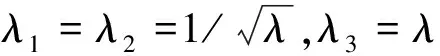
研究表明，介電彈性體材料的介電常數ε會隨著預拉伸率、激勵頻率、電極材料以及環境溫度的變化而變化。本文采用文獻[9]推導的公式來考慮材料介電常數變化產生的影響，即：

(4)

因此，系統亥姆霍茲自由能的變化可表示為：

(5)

介電彈性體驅動單元的電荷量可表示為：

(6)

則系統電勢變化所做的功為：

(7)

系統中慣性力所做的功為：

(8)

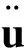
將式(1)代入(8)可得：

(9)

聯立式(2)、(4)、(5)、(7)、(8)和(9)可得：

(10)

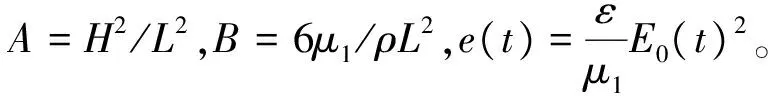
3 介電彈性體驅動單元的動態特性

為了研究介電彈性體驅動單元的動態響應，本文基于四階-五階Runge-Kutta算法(ode45)，采用Matlab軟件求解運動方程(10)，數學簡化模型以VHB4910材料

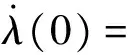
表1 VHB4910材料相關參數

3.1 恒定電場強度下驅動單元的動態響應

取H=0.5mm，L=5mm，對介電彈性體驅動單元施加不同的名義電場強度E0，分別為10kV/mm、15kV/mm、20kV/mm和22.13kV/mm，系統的動態響應見圖2。

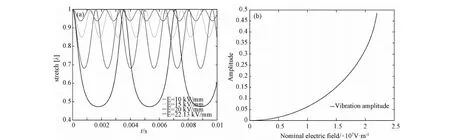
圖2 不同場強下驅動單元的動態響應 (a) 振動； (b) 振幅-場強關系圖Fig.2 Dynamic response of DE actuating unit under different electric fields (a) Vibration; (b) Relationship between amplitude and electric field

由圖2可知，電場強度是影響介電彈性體驅動單元動態響應的重要因素，即增大場強，系統的振幅將隨之增大、振動頻率將隨之減小。當場強達到臨界值22.13kV/mm時，模型的振幅達到最大值49%，此時如果場強繼續增大，系統將失穩。此外，由于存在材料粘彈性、機電耦合等因素的影響，系統振幅與場強的關系呈現明顯的非線性特征，即隨著場強的增大，系統振幅增大的速度將越來越快。

3.2 簡諧變化場強下驅動單元的動態響應

當場強隨時間發生變化時，介電彈性體驅動單元的動態響應則比較復雜。假設名義電場強度E0為：

(11)

式中：EA為電場強度的幅值，f為頻率。

取介電彈性體驅動單元的尺寸H=0.5mm，L=5mm，當電場強度幅值EA分別為10kV/mm、14kV/mm和18kV/mm，頻率f的變化范圍為1Hz到1kHz時，系統振幅與頻率的關系見圖3。

圖3 不同電場強度下驅動單元動態響應的幅頻特性曲線Fig.3 Frequency-amplitude curve of actuating unit’s dynamic response under different electric fields

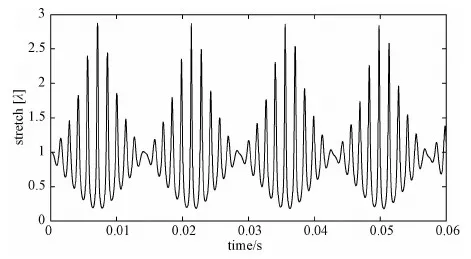
圖4 EA=18kV/mm, f=386Hz時，驅動單元的動態響應Fig.4 Dynamic response of actuating unit under the electric field of 18kV/mm and frequency of 386Hz

由圖3可知，在不同電場強度條件下，介電彈性體驅動單元幅頻特性的整體變化趨勢基本一致，即系統的振幅隨著頻率的增大達到峰值，然后隨著頻率繼續增大而下降，最終趨于穩定。其中，當EA=18kV/mm，f=386Hz時，系統將發生共振，其頻響特性曲線見圖4，可見系統此時的振動十分劇烈。當EA分別為10kV/mm、14kV/mm和18kV/mm時，系統振幅的波峰對應的頻率分別為440Hz，426Hz和386Hz，表明系統在該頻率附近產生共振，且共振頻率隨電場強度的增大而減小。

3.3 幾何尺寸對驅動單元動態響應的影響

對介電彈性體驅動單元模型施加22.13kv/mm的電場強度，取L=1mm，當材料厚度同平面尺寸的比值H/L分別取0.5，1和2時，系統的動態響應見圖5。

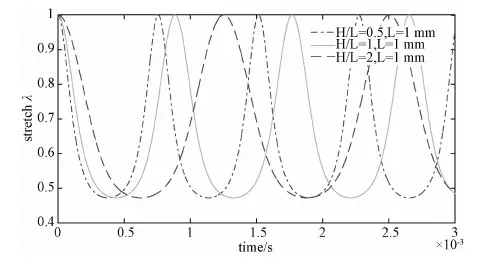
圖5 幾何尺寸對驅動單元動態響應的影響Fig.5 Influence of geometry on the dynamic response of actuating unit

由圖5可知，當電場強度恒定時，幾何尺寸是影響介電彈性體驅動單元振動頻率的重要因素，即系統的振動頻率隨H/L的增大而減小；當H/L取不同值時，系統動態響應的振幅保持不變。因此，介電彈性體驅動單元動態響應的振幅由電場強度決定，與材料厚度對平面尺寸的比值無關。

4 結 論

本文以介電彈性體驅動器(DEA)的基本驅動單

元為研究對象，從熱力學能量轉化的角度得到了基于Ogden應變能函數的介電彈性體驅動單元的二階常微分運動方程，分析了系統在恒定和簡諧電場強度情況下的動態響應及模型幾何尺寸的影響。結果表明：在恒定場強下，隨著電場強度幅值的增大，驅動單元的振幅將隨之增大、振動頻率將隨之減小；在簡諧場強下，隨著電場強度頻率的增大，驅動單元將發生共振，且共振頻率將隨之減小。此外，介電彈性體驅動單元動態響應的振幅由電場強度決定，與材料厚度對平面尺寸的比值無關。綜上所述，本文的理論分析方法能夠較好地模擬電壓載荷下介電彈性體驅動單元的動態響應，可以為下一步新型介電彈性體驅動器的設計提供參考。

[ 1] 楊丹, 張立群. 高電致形變介電彈性體的研究進展[J]. 材料保護， 2013, 46: 92～95.

[ 2] Biggs J, Danielmeier K, et al. Electroactive Polymers: Developments of and Perspectives for Dielectric Elastomers[J]. Angew. Chem. Int. Ed., 2013, 52: 9409～9421.

[ 3] Dubois P, Rosset S, Niklaus M, Dadras M, Shea H. Voltage Control of the Resonance Frequency of DEAP Membranes[J]. J. Microelectronmech. S., 2008, 17: 1072～1081.

[ 4] Zhu J, Cai S, Suo Z. Nonlinear Oscillation of a Dielectric Elastomer Ballon[J]. Polym. Int., 2009, 59: 378～383.

[ 5] Zhu J, Cai S, Suo Z. Resonant Behavior of a Membrane of a Dielectric Elastomer[J]. Int. J. Solids Structures, 2010, 47: 3254～4362.

[ 6] Fox J W, Goulbourne N C. On the Dynamic Electromechanical Loading of Dielectric Elastomer Membranes[J]. J. Mech. Phys. Solids, 2008, 56: 2669～2686.

[ 7] Xu B X, Mueller R, Theis A, Klassen M, Gross D. Dynamic Analysis of Dielectric Elastomer Actuators[J]. Appl. Phys. Lett., 2012, 100, 112903.

[ 8] 朱銀龍. 介電型EAP換能器機電耦合特性研究[D]. 南京航空航天大學博士學位論文, 趙東標, 南京, 2012.09.

[ 9] 朱黎輝. 電活性介電彈性體膜型材料電致應變特性的研究[D]. 吉林大學博士學位論文, 朱喜林, 長春, 2011.06.