數學理性：數學學習的至高訴求

鄭壽寶

[摘 要]數學學習除了包含數學知識、方法、規律等學習內容外，還應有數學精神的培養，數學理性精神當屬數學學習的至高訴求。從數學理性的要義出發，在“研究數學的理性”和“理性的研究態度”層面闡明具備數學理性的要旨，給出培養學生數學理性的方法和策略。

[關鍵詞]數學理性；數學學習；研究態度

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2018）05-0009-02

數學作為人類文化的一部分，包含數學的知識、方法、語言、思想、精神等，特別是在自然科學和社會科學發展的過程中，數學將其理性精神發揮得淋漓盡致，僅為人類的發展提供了理性的思維方式和工具。故，對數學的學習，實則是對數學理性的追求。

數學理性一般體現在以下幾個方面：第一，客觀的、理智的研究立場。數學研究的對象并非客觀世界中真實存在的，而是人類抽象思維的產物，但是在研究中，我們應當采取純客觀的立場，通過嚴格的邏輯分析去揭示其內在的性質。第二，精確的、定量的思維方式。數學理性的“數學味”就體現在它的“精確”“定量”上，不應含糊，這既是科學研究的基本方法，也是科學研究的基本目標。第三，批判的、開放的理性精神。批判的精神讓我們能時刻提醒自己不要淪為權威主義者，而要用可靠的論證來進行判斷。

明確“數學理性”范疇后，要做的就是讓學習者具備“數學理性”。基于理性的客觀性、學習者的主觀性，具備“數學理性”的要旨可概括為“客觀”和“主觀”，即”研究數學的理性“和”理性的研究態度“。

一、引導學生抽象出數學的本質

“抽象”是數學的特性，“抽象出數學本質”則是數學理性所在。

如教學蘇教版教材三年級上冊“倍的認識”時，學生通過條件“藍花有2朵，黃花有6朵”就能感受到“黃花的朵數是藍花的3倍”，也能通過“藍花有2朵，紅花有8朵”感受到“紅花的朵數是藍花的4倍”等倍數關系，至此，對于學生來說，“倍”還只是一個表象認識，而對于為什么“一個數是另一個數的幾倍”還不清楚，學生的認知上缺一個“倍”的抽象過程。“擺一擺、畫一畫”則給學生抽象出“倍”的含義提供了途徑。擺：擺出2朵藍花、6朵黃花，為了能看出黃花的朵數是藍花的3倍，擺的同時還需體現出“份數對應”，如圖1。

把圈中的花拿走后（如圖2），從僅有兩種數量，到對應份數，再到留下的“圈”，這是逐步抽象的過程，也是逐步厘清“倍”的本質的過程。“畫一畫”也是抽象出“倍”本質的途徑，具體思維過程亦是從表象到本質，這里就不展開說明了。

以上課例反映了數學的學習不是停留在表面而是要抽象出本質，這正是數學理性使然。

二、讓學生經歷數學結論形成的過程

數學學習包含對數學結論、公式等結果的認知，更需經歷基本的活動過程，積累基本的活動經驗，尤其是小學數學，“還原數學結論形成的過程”是學習數學的理性思考，即明白“所以然”。

如教學蘇教版教材五年級下冊“圓面積計算方法”時， “圓面積等于半徑的平方乘圓周率”這個計算方法并不復雜，學生都能夠運用公式解決問題。這節課教學的核心在哪里？是用它來解決問題，還是探索出公式形成的過程？顯然后者是每一個教師的用心所在。教師可以“怎樣計算出圓這種曲線圍成的圖形面積呢？”為切入點進行教學，學生可能會受到之前研究圖形面積方法的影響選擇用數方格的方式開展研究，但一定會發現“數方格”的方式所得到的面積不準確，因為是曲線圍成的圖形，將“曲線圖形”轉換成“直線圖形”是此時研究面積的內在需要，至此，將圓轉化為長方形繼續研究，圓的面積計算方法也應運而生。這個探索過程給了學生一個“明白圓的面積為什么這樣算”的答案，也是一次學生自我還原知識結論形成的過程，即知道了“所以然”。其實“還原數學結論形成的過程”不僅在面積計算的教學中有所體現，乘法口訣的教學、單位進率的學習、分數的理解等無不重視“所以然”，明白了數學中的“所以然”，才能明晰數學的理性。

三、讓學生體悟數學的邏輯性

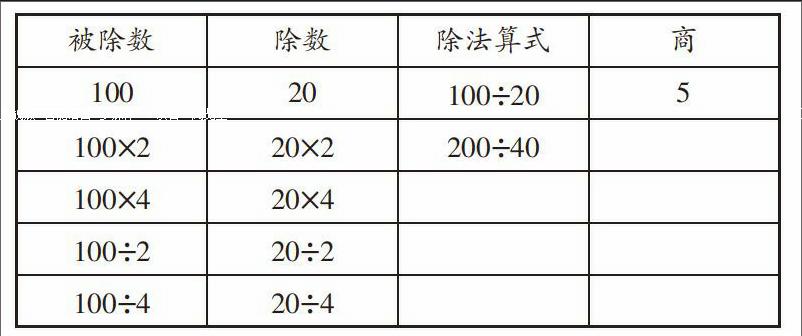
能體悟數學的邏輯性是理解數學的關鍵，也是數學理性的彰顯。如“商不變的性質”的教學中，學生通過下表中對除法算式的計算、觀察、交流、推理、發現等過程，就能從除法算式的共同點推出一般性結論：在除法里，被除數和除數都乘或除以同一個數（0除外），商不變。

整個學習過程是一個歸納、推理的過程，是從一般性中尋找共性的過程，學生在學習的過程中不僅形成了結論，更體悟了數學的邏輯性。

又如，根據平行四邊形“兩組對邊分別平行且相等，對角相等”的特點，能推出“只有一組對邊平行的四邊形不是平行四邊形”“有一組對邊不相等的四邊形不是平行四邊形”，也能做出“因長方形對邊平行且相等、四角相等，所以屬于平行四邊形”等判斷。

四、讓學生體悟理性的研究態度

1.了然“是什么”

“理性”的態度首先是了然“是什么”。研究數學的任何一種元素，都需從其“是什么”開始。如學習平行四邊形的性質時，學生在操作、猜測、合作、交流后基本能探索出“對邊平行且相等、對角相等”等平行四邊形的獨有特質；又如“3x和33”，“3x”表示的是“3乘x”，而“33”則是3個十和3個一的和。這些即是研究的第一個層面——了然“是什么”，是理性的開始。

2.追尋“為什么”

“理性”的態度其次是追尋“為什么”。蘋果掉在地上，我們會習以為常，而蘋果砸在了牛頓頭上，他卻追問“為什么蘋果會往地面掉落而不是往空中飛”，萬有引力定律據此被他發現，這是理性的研究態度帶來的發現。數學學習，“理性地追尋為什么”是下一個發現的開始，數學皇冠上的明珠“哥德巴赫猜想”的內容都已經十分清楚了，當屬“是什么”，但數學研究者并未停止探索，仍苦苦去追尋“為什么”，正因為有這樣理性的態度，陳景潤方摘得桂冠，數學才能得到一次次的發展。

克萊因說：“數學是一種理性的精神，使人類的思維得以運用到最完善的程度。”數學學習學什么，數學學習的訴求在哪里，數學理性當屬我們思考并實踐的方向。數學理性帶給學生的不僅僅是純粹的數學知識，更是一種精神，能夠引導學生在多維學科中深度學習。

[ 參 考 文 獻 ]

[1] 曹培英. 小學數學學科核心素養及其培育的基本路徑[J]. 課程·教材·教法， 2017（2）.

[2] 史寧中.學科核心素養的培養與教學——以數學學科核心素養的培養為例[J]. 中小學管理， 2017（1）.

[3] 周衛東.必備品格：數學核心素養的重要維度[J].河北教育，2017（1）.

[4] 吳增基，張之滄，錢再見，等.理性精神的呼喚[M].上海：上海人民出版社， 2001.

（責編 童 夏）