設計開放性數學作業 促進學生差異發展

□林 俊

“學生的學習，除了聽老師的講解以外，還要靠反復不斷的練習。獲取知識需要練習，掌握本領更需要練習。”反映的是 “掌握知識、形成技能”的傳統作業設計理念。現實中出現的 “作業布置得多、學生做得苦、教師批改得累”的現象，往往是以理解知識和強化技能為指向的，折射的是教師作業設計理念的落后和作業設計能力的缺失。如何避免機械、重復、單調、乏味的低效作業？練什么、怎么練則是繞不過去的兩個核心問題。 “怎么練，練什么內容更有意義，要靠老師來設計。”顯然，作業設計教師不可缺席，旁人無法代替！ “教師設計得好，指導得法，學生事半功倍；教師設計得不好，指導不得法，學生事倍功半。”可見，在作業設計中，教師責任重大、責無旁貸。

傳統作業內容機械重復，缺乏挑戰性；作業形式呆板枯燥，缺乏趣味性；要求統一僵化，缺乏靈活性。這種落后的作業形式降低了學生的熱情，固化了學生的思維，壓抑了學生的個性，也與數學課程標準“使不同的人在數學上得到不同的發展”理念相悖。因此，新課改背景下的作業設計應以發展學生的數學核心素養為指南，理念可以前衛一點，內容可以開放一點，要求可以靈活一點，設計開放題就是一個很好的切入點。

答案不固定、條件不完備或者策略多樣化的習題，稱為開放題，它是與封閉題相對的。目前教材中的開放題還不多，教師需進行設計。設計開放題既可以利用陳題改編，又可以通過對現有開放題的加工得到，還可以根據需要自己獨立設計。一份優質的數學作業往往能體現教師一定的專業水平和學術水準。

一、設計情境開放的數學作業，促進學生差異發展

學習的最大動力乃是對所學材料的興趣。小學生受年齡和心理限制，他們喜歡新穎有趣、形式多樣和貼近生活的作業。精心選擇現實生活中的材料，設計一些包含情境的數學問題，對于激發學生的求知欲，調動學生的學習積極性大有好處。

翻開教材或各種練習冊、試卷，計算類似16×79、2790÷90的練習題比比皆是。如此習題，雖然能有效地訓練學生 “兩位數乘兩位數”和 “除數是兩位數的除法”的相關技能，但如果經常做這種枯燥的練習，學生就會覺得數學面目可憎，作業索然無味。因此，筆者認為不妨作如下包裝、設計：

列豎式計算下面各題，并將計算結果填到等號后，使等式成立，同時將結果填入短文中，使短文信息完整。

722÷38= 121×16= 130÷26=

209×9= 1210÷22= 317×6=

你知道嗎？魯迅是中國偉大的文學家、思想家和革命家。原名周樹人，字豫才，浙江紹興人。___年出身于破落封建家庭。 ___年前往日本學醫，后棄醫從文。 ____18年____月，首次用筆名 “魯迅”發表中國現代文學史上第一篇白話小說 《狂人日記》。 ____年10月病逝于上海，終年____歲。

改造后的練習題，有著濃濃的文化味，在鞏固數學知識的同時也與語文學科建立了聯系。學生要把這6道題的答案：19，1936，5，1881，55，1902填入介紹魯迅生平的文字中，既要運用過去學習的年月日知識，又要進行合情推理，由此便拓展了學生的知識面，提高了學生的思維能力。這種別出心裁的設計，使學生感到練習有趣而不乏味、有挑戰而不簡單。

單調、劃一的傳統作業題型，往往容易引起視覺疲勞，使學生產生消極應付的心理。如果變換一下題型，從形式到內容來個 “大變臉”，就會使人耳目一新，喜聞樂見，最大限度地吸引學生參與。

如：學習 “百分數”后，就可設計題型，讓學生在優美詩文中計算百分數問題。

春水春池滿，春時春草生，

春人飲春酒，春鳥弄春色。

（1）請朗誦這首詩，看看哪個字出現得最多？

（2）“春”字出現的次數占全詩總字數的百分之幾？

（3）課后找一首詩，使某一個字出現的次數至少占10%，然后有感情地朗讀。

這個練習沒有止于單純的紙筆計算練習，而是融“百分數”的計算于優美、開放的詩文情境之中，學生既要找詩，又要讀詩，還要計算。語、數結合，趣味無窮。海量的資料檢索、不同的詩詞閱讀、具體的數學運算等實踐活動形式，大大豐富了學生的學習方式。

再如 “小數加減法”的課后作業，提供了一家快餐店的午餐食譜，同時標明每種食物的蛋白質含量。

（1）根據自己的口味和飯量選餐，并列豎式計算所訂飯菜蛋白質的總含量。

（2）營養學家經過一系列調查研究后發現：7~10歲的兒童一頓飯的蛋白質含量大約需要22.5克。把自己選餐中的蛋白質總量和標準比一比，看是高了，還是低了，并計算相差多少。

（3）看到比較結果，想想你以后選餐需要注意什么。

這樣的作業，因為與學生的現實生活緊密相連，所以他們興致很高；因為與學生的營養狀況息息相關，他們都想知道自己喜歡的飯菜蛋白質含量是多少，是否符合規定的標準，所以他們迫不及待地想做。這樣的作業自然增強了學生合理膳食的意識，將枯燥的計算與情境相融，很好地調動了學生的學習熱情。

二、設計條件開放的數學作業，促進學生差異發展

數學教學的根本目的是教會學生思考，而設計具有低起點、寬入口、有挑戰的開放題，能夠在傳授知識、訓練技能的同時，更好地滲透數學思想方法。設計一些具有現實意義、思考價值的開放題——條件開放題、問題開放題、結論開放題及策略開放題，可以面對不同學生的學習現實，促進不同學生的適度提升。條件開放題可以從改編現有封閉題的條件得到，十分方便、快捷。

如：三名選手跳遠的成績：A.3.84米；B.4.01米；C.3.□9米。

（1）誰是第一名，誰是第二名？

（2）如果A是第二名，□里可以填哪些？

（3）如果C是第二名，□里可以填哪些數？

此題由封閉題 “三名選手跳遠的成績：A.3.84米；B.4.01米；C.3.89米。誰是第一名，誰是第二名？”改編而來。把封閉題的一個條件3.89的十分位留白，任學生思維自由馳騁，使每個學生都有得說，有得講，滿足了學生的不同需要。不僅使學生在相互交流中對小數比較大小的方法理解得更加透徹，而且在分析問題、解決問題中滲透了分類思想。

再如：小華家離學校125米，小青家離學校175米，小華家與小青家之間相距多少米？

原題配有插圖 （學校在兩家之間，且在同一直線上），思維含量不高，學生只需看圖列式即可解決問題，涉及的只是低層次思維。當把教材中的插圖去掉后得到的條件開放題，思維附加值明顯提高。這樣，為不同水平的學生提供了展示聰明才智的廣闊舞臺。

（1）小華家、小青家和學校都在一條直線上，并且都在學校的一側，則兩家相距175-125=50（米）；

（2）小華家、小青家和學校都在一條直線上，并且分散在學校的兩側，則兩家相距125+175=300（米）；

（3）小華家、小青家和學校都不在一條直線上，則兩家的距離大于50米，而小于300米。

多數學生受固有思維慣性的影響，可能只是考慮了上述情況 （1）或（2），頭腦靈活一點的學生能夠考慮這兩種情況，水平較高的學生則可能考慮到情況 （3），但不會用圓環圖完整地表達所有的情形。通過生生互動，相互補充、不斷完善，形成了完整的認知視角；經過教師引領，師生互動，學生思維從片面走向全面，從具體走向抽象，從零散走向統整，令不同層次的學生眼界大開，受到思維風暴的洗禮。

三、設計要求開放的數學作業，促進學生差異發展

由于受多重因素的影響，學生在數學基礎、經驗和能力等方面都存在差異。為此，設計作業時，不能“一刀切” “齊步走”，而應該從學生的數學現實出發，針對學生的個體差異設計彈性化作業，為每個學生創造一個寬松、自主的練習，提高和發展的人文環境，使每個學生都成為學習的主人，品嘗到成功的喜悅，在數學學習歷程中不斷獲得前進的動力。

如新授課上，為了幫助學生記憶和理解公式，培養學生靈活思維的能力，運用公式S=πr2求圓面積時，可設計以下A、B、C三個層次的練習，供不同層次的學生選擇。

按照美國教育心理學家B.S.布盧姆掌握學習理論，我們把教學目標 （認知目標）水平由低到高分為以下5個層次：識記、領會、簡單運用、綜合運用和創見。不同層次的學生有不同的選擇空間，也有相應的達標要求：學困生至少應該達到A層 （簡單運用水平），中等生要達到B層 （綜合運用水平），優等生力求達到C層 （創見水平）。

還可以根據不同層次的學生設計模仿練習、變式練習和發展練習三類，學生根據自己的實際情況自由選擇適合自己需要的作業。如學習 “長方體和正方體的認識”之后，設計了如下難度漸增的作業：

★一個長方體紙盒的長是5厘米、寬是4厘米、高是3厘米，做這個紙盒需要多少平方厘米的紙？它的體積是多少？

★★一個長方體紙盒的棱長總和是48厘米，長是5厘米、寬是4厘米，它的體積是多少？

★★★一個長方體紙盒的底面積是20平方厘米，底面周長是18厘米，它的表面積是94平方厘米，它的體積是多少？

再如：學習 “億以內數的認識”后，設計難易不等、彈性極大的開放作業：

用4個 “8”和4個 “0” 擺一擺。

★擺出不同的幾個數，寫下來，再讀一讀。

★★按要求擺一個數，寫下來，再讀一讀。

（1）一個 “0”都不讀出來的八位數；

（2）只讀出一個 “0”的八位數；

（3）讀出兩個 “0”的八位數；

（4）讀出三個 “0”的八位數。

★★★按二星級的要求擺出所有的數，寫下來，再讀一讀。

這種作業可以讓不同層次的學生找到適合自己的作業，調動了學生做作業的積極性，樹立了學習數學的自信心，享受到作業成功的樂趣。

在 “減負”背景下，還可以在控制作業總量的情況下，通過制訂作業選擇的規則，鼓勵學生完成更具思考性、挑戰性的作業，激發自我效能。如 “長方形和正方形的面積”綜合練習，8題為一組，其中有6題為一星題、1題為二星題、1題為三星題，由學生自由選擇、組合題目來完成6顆星。

★★★從邊長10厘米的正方形紙上，剪去一個長3厘米，寬2厘米的長方形，剩下的紙片面積是多少？周長呢？

★★一塊長方形和一塊正方形的面積相等。已知正方形的邊長是6厘米，長方形的寬是4厘米。求長方形的周長。

★一個長方形寬5厘米，長是寬的2倍。求它的周長和面積。

★一個長方形長10分米，寬比長短2分米。求它的面積。

★一個正方形周長是12厘米，它的邊長是多少？面積是多少？

★一個長方形面積是48平方分米，寬是6分米，長是多少？

★一個長方形長40厘米，寬3分米，求它的面積。

★一個長方形長6厘米，寬4厘米，它的周長和面積各是多少？

四、設計表征開放的數學作業，促進學生差異發展

表征是學生對問題內隱思考的外在表達，不同學生表征的方式方法是有差異的。表征開放實質上就是解題方式、方法的開放。表征開放的數學作業，為不同學生展露自己的思想、才華提供了大顯身手的機會。表征開放的數學作業，教材或配套練習中有的，我們要慧眼識珠，為我所用；如果沒有，要加以收集、設計，以更好地照顧學生差異、暴露學生差異、展示學生差異、利用學生差異，在群體交流、互動中，相互欣賞、品味、質疑、碰撞，促進學生差異發展。

一道淺顯的題目，也能反映不同學生的思維風格：

圖1

圖1是用語言表征的。可以看出，答題者是邊審題邊表征的：看到 “小芳比小云輕一些”，寫下 （比）“26kg少”；看到 “小強比小云重一些”，寫下 （比）“26kg多”。表達如此及時、簡潔。

圖2

圖2也是用語言表征的，但與圖1的區別在于：答題者不是把簡潔的表達寫在與條件對應的題目之中，而是寫在一起的。可以看出寫的時候是邊寫邊想的，哪個寫在26前，哪個寫在26后。這樣按照一定的順序、特定的邏輯排好之后，答案就自然顯現出來了。

圖3

圖3是用圖形表征的。答題者用一條線段表示小云體重26kg，體重比小云輕的線段就畫短一點，比小云重的線段就畫長一點。誰最重、最輕看線段的長短一目了然。

再如，學習 “三位數除以一位數” （口算）后，作業中出現了一道思考題。

圖4中的大長方形表示420，涂色部分表示多少？

圖4

雖然學生答案是一致的，但是想法卻多種多樣，這可以從他們不同的表征中窺見端倪。

圖5

圖5一簡一繁、一明一暗。左邊用圖示清楚地表達了陰影部分 （三角形）轉化為長方形的過程，而右邊則惜墨如金， “6格”二字就高度概括了轉化的過程。

圖6

圖6的2個答題者雖然都把空白的小三角形涂成了黑色，都把陰影部分 （三角形）轉化為長方形了，但左邊是表示把右邊的三角形割下來補到下邊，右邊表示的是這兩個三角形是完全相同的。

圖7

顯然，圖7傳遞的信息與圖6左邊表達的意思更加接近，用箭頭清楚地表示出割補、旋轉的過程。

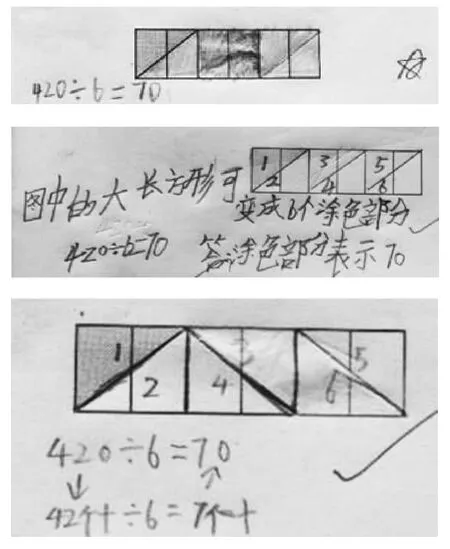
圖8

正如學生所言， “圖8中的長方形可變成6個涂色部分。”但具體表達有細微差別，有用色彩表示的，有用線段分割的；分割線的方向也有不同。

圖9

圖10

圖9、圖10中，為什么答題者還用三道算式表示？這兩個解答看似多此一舉，其實與上面的思路還是不同的。他們是先求出每個小長方形的大小，再求出兩個小長方形的大小，最后再求陰影部分的大小（圖1中的表征就標示得非常清楚）。因為陰影部分是兩個小長方形組成的較大長方形的一半，這可從圖10的表征得到印證。

圖11中，答題者的思路與上面的截然不同，他們看到的等量關系是陰影部分等于它所在長方形的一半，而不是把陰影部分轉化成長方形。

圖11

圖12中，答題者思路更具獨特性：別人看到的是大長方形里有6個小長方形，而他看到的則是3個長方形。他在思考時，能夠始終指向問題，壓縮思維步驟，這是難能可貴的。雖計算有誤，但我還是照樣獎勵了一個五角星。

圖12

[1]陳樸，潘自由，等．怎樣設計小學生的練習和作業［M]．南京：江蘇教育出版社，1987．

[2]肖川主編．名師作業設計經驗［M]．北京：教育科學出版社，2007．

[3]方臻，夏雪梅編著．作業設計——基于學生心理機制的學習反饋［M]．北京：教育科學出版社，2014．

[4]林俊．數學作業設計的走向：超越傳統［N]．中國教育報，2013－3－27．

[5]希文．這樣的習題好［J]．小學數學教師，2005，（6）．