一道奧林匹克問題的推廣及拓展

孫丕訓 張留杰

北京市陳經綸中學 (100020)

筆者在閱讀文[1]時，發現此問題內涵豐富、規律性較強，于是對此問題進行了更加深入的思考，與大家共勉．

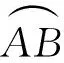
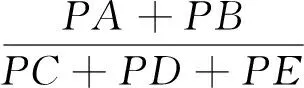
一、問題的推廣

我們先從特殊的正多邊形入手思考，不難得出：

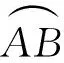
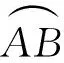
即便結合正五邊形時的結論，也不易猜想出一般規律，于是我們類比文[1]中的證明方法，先探究正n邊形時的結論．

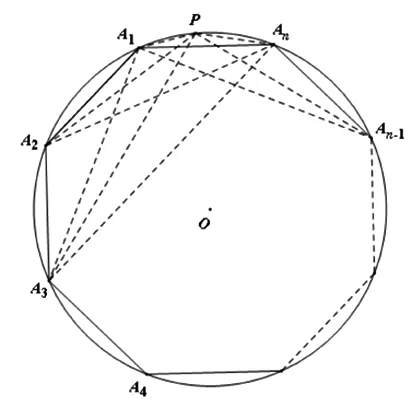
圖1

=an-1(ai>0，i=1,2,…,n-1)，PA1=x1，PA2=x2，…，PAn=xn(xi>0，i=1,2,…,n)．

分別在四邊形PA1A2An、PA1A3An、…、PA1An-1An中，運用托勒密定理，可得

A1An·PA2=PA1·A2An+A1A2·PAn、A1An·PA3=PA1·A3An+A1A3·PAn、…、A1An·PAn-1=PA1·An-1An+A1An-1·PAn，注意到正n邊形中A1An=A1A2=a1，A2An=A1A3=a2，…，等相等關系，所以有a1x2=a2x1+a1xn、a1x3=a3x1+a2xn、…、a1xn-1=an-1x1+an-2xn，將這n-2個式子相加，得a1(x2+x3+…+xn-1)=(a2+a3+…+an-1)x1+(a1+a2+…+an-2)xn，

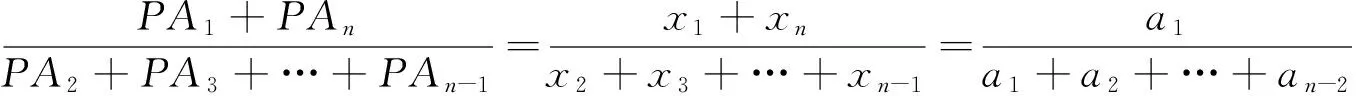
下面求這個定值．

設正多邊形A1A2…An的外接圓O的半徑為R，

圖2

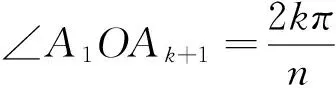
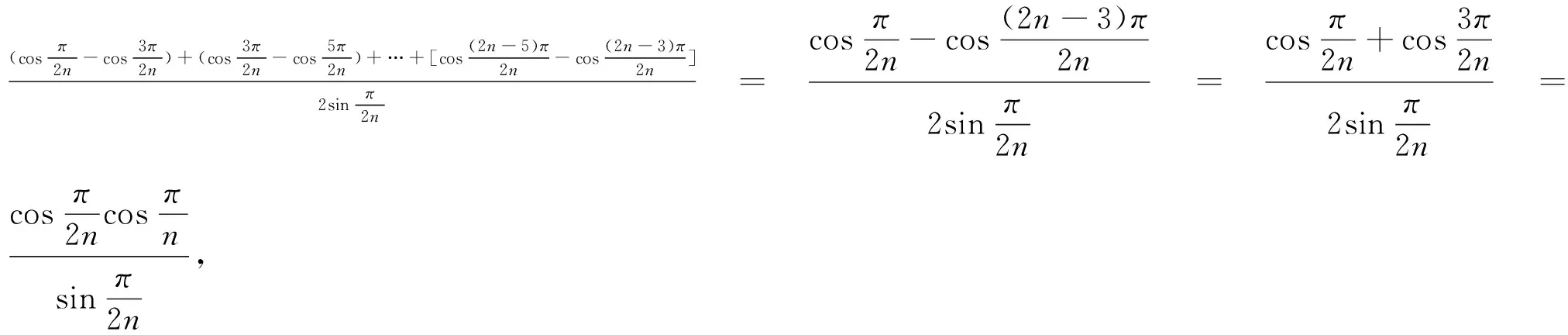
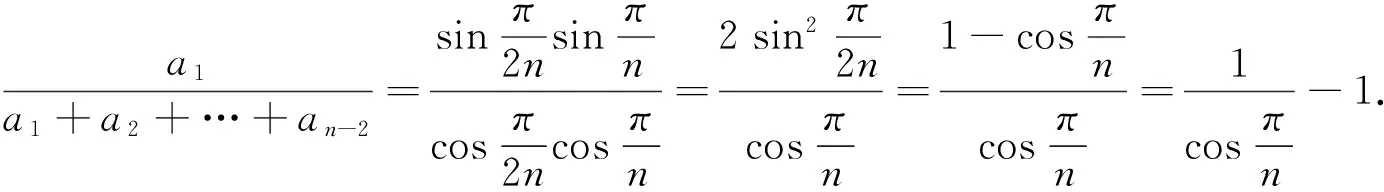
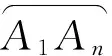
二、問題的拓展

我們知道，點是圓的極限圖形，將點“膨脹”為圓，或將圓“收縮”為點，可以命制具有新意的問題，文[2]將圓內接四邊形的頂點“膨脹”為圓，對托勒密定理進行了如下拓展：

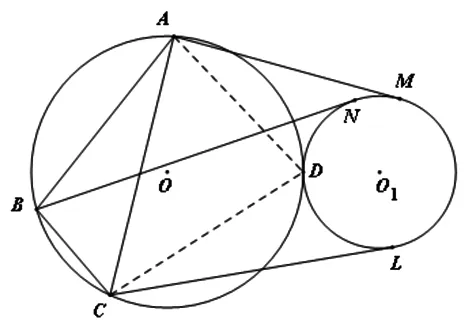
圖3

托勒密定理的推廣：如圖3，已知點A、B、C、D在⊙O上，⊙O1外切⊙O于點D，AM、BN、CL分別切⊙O1于點M、N、L．則AB·CL+BC·AM=AC·BN．

根據文[2]中的推廣，我們也可以將結論1進行類似拓展，于是有

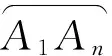
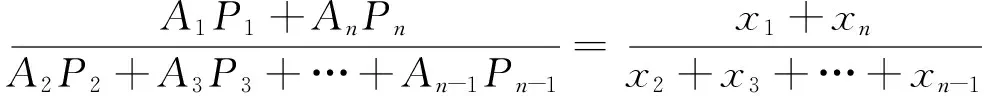
[1]黃金福.數學奧林匹克問題.高536[J].中等數學.2017.8.

[2]張留杰,邱繼勇.第1578問題的簡證、推廣及應用[J].數學通報.2006.7.60-61.