高中數學教學生學會解題的策略研究

☉廣東省廣州市番禺區石樓中學 劉新萍

教會學生在解題中怎樣探尋解題突破與思路是值得廣大高中數學教師尤為重視的課題.有些教師面對課堂教學中的例題往往會直接進行求解，這樣的做法往往會令學生的思維形成定式且不能拓展.本文結合解題指導的順序與實際案例對解題應有的策略進行了大概的分析.

一、引導學生“先估后算”

面對實際問題首先進行粗略估計是解題中的第一步，這一“初步定向”的審題步驟主要鍛煉的是學生面對問題時的洞察力.比如，在已知直角三角形中的兩個獨立條件的情況下進行問題的求解，往往利用勾股定理與三角比知識就可以解決問題，而條件不夠、問題又不確定時就應該采用方程來解決了.

先估后算一般包含條件與數量這兩方面的估計.

1.條件的估計

條件的估計包含條件是否多余或缺少、是否存在矛盾、是否可變等主要的內容.

例1 如圖1，已知△ABC中，AM是BC上的中線，CN⊥AM，BC=2，沿AM將△CAN翻折到△AND，說出BD與BC數量關系.

部分學生思路如下：MN是△BCD的中位線，所以比較MN和MC即可比較出BD和BC，且AM⊥CD，所以斜邊MC＞MN，即BC＞BD，但參考答案卻是BC=BD.于是他想證明∠CBD=45°，但最終沒能證明.

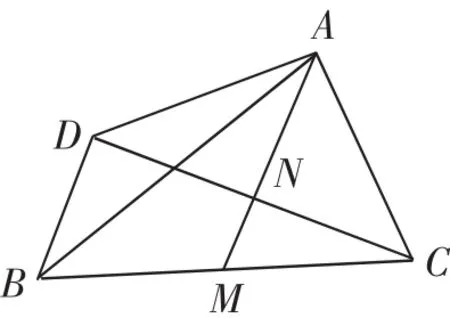
圖1

事實上，想證明∠CBD=45°，就是證明∠CMN=45°，這是中線AM與BC的夾角，題中并沒有談及它等于45°，雖然進行了一定的翻轉等操作，但它不會變成45°.

因此，基本量不足的情況下問題是可變的.

2.數量的估計

基本量不足導致問題可變時就應該首先搞清楚問題中究竟有哪些量，然后再去分析固定的量、變的量、初始量、會跟著變的量、這些量的變化范圍等等.

例2 用50米的材料圍成一飼養場并使其面積最大，應該怎樣圍？

有些學生解題如圖2所示，設寬為x，列式y=x（50-2x），然后求函數最大值.

學生在此類題目剛剛出現時就接觸列函數式的解法往往不能適應，教師應這樣分析：

當寬x=1米，長為50-2x=48米，面積為S=1×48=48平方米；

當寬x=2米，長為50-2x=46米，面積為S=2×46=92平方米；

……

學生在教師的推理分析中很快能夠明白S是隨著x的變化而變化的.教師如果能夠經常引導學生對這方面進行關注，學生在長久的訓練中就會逐步養成分析變量、常量的習慣，理解題意時的效果就會更好.

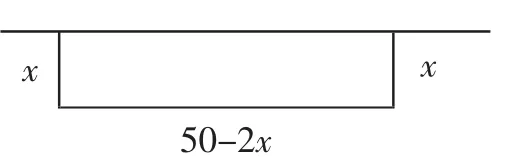
圖2

二、引導學生模式識別，探求優法

教師引導學生在初步估計之后進行解題的思考便是模式識別這一步驟了，學生一旦能夠領略并使用模式識別的策略，常規題的解決將會取得尤為欣喜的效率與效果.做過的范例以及自己歸納的解題模式等等都屬于解題的一些模式.教師在解題教學時應幫助學生理解其中蘊含的思想方法這一模式的靈魂，幫助學生正確掌握解題的步驟，避免亂套無用模式，使得學生在常規題的解決中做到快速而準確.如數列是高考中的重點內容，解決這些相關問題時，主要思路：1.聯立方程組（或不等式組），通過解方程組（或不等式組）來求解；2.選擇恰當的變量建立目標函數，再用函數的知識來解決問題.

例3 等比數列{an}中，S2=2，S4=8，則S6=（ ）.

A.-32 B.32 C.-26 D.26

等比數列中有五個量a1，n，q，an，Sn，一般可以“知三求二”，通過列方程（組）求關鍵量a1和q，問題可迎刃而解.

掌握通法之后還應該對優法進行一定的探求，本題還可以利用等比數列的性質來求解，教師在解題教學時應幫助學生逐步鍛煉出一眼看穿問題本質的能力并投入應用中，注重數學思想方法的培養對于學生解題能力的培養很有意義.

解析：因為S2，S4-S2，S6-S4成等比數列，

所以（S4-S2）2=S2（S6-S4），

所以36=2（S6-8），S6=26.

有些具體問題雖然由幾個內容組成，但解題時有意放大視角并將研究對象看成為一個整體來使問題得以求解即是這里所指的整體思維.研究問題的形式、結構以及處理得到整體視角的分析往往能令解題變得更加簡潔而順利，教師在平日的教學中也應有意識地培養學生整體思維的意識與習慣.例4 5a2+25a+9=0，9b2+25b+5=0，求.

從問題呈現的整體形式看，學生通過觀察可知，兩式子系數對稱，將9b2+25b+1=0兩端除以b2，得5 （）2+25）+9=0，可知a和是方程5x2+25x+9=0的兩根，利用韋達定理可知，.

對于內部構造與機理不能直接觀察的事物或系統在系統科學的范疇里被稱為黑箱，而那些部分機理還是明確的則稱為灰箱.黑箱原理的基本思想在于借助外部考察輸入黑箱與其輸出反饋信息之間的變化關系來探求問題結果，中學數學中的問題大多為已知部分機理的“灰箱”.

三、引導學生多元化分析條件結論

如果通法、優法尤其是“一眼看穿”的方法在某問題的解決中都行不通，這時候只好對題中的條件、結論等進行仔細的分析了，這就是本文所要討論的雙向分析與差異分析等策略了.

1.雙向分析策略

雙向分析就是指把已知條件及其伸展、結論的倒溯這兩個方面結合起來進行分析并最終找到解題的中間環節而獲求解的方法.

簡單說來，就是借助條件A進行正面、順向的思考并得到經過一定理解或轉化的條件B1，B2，B3，…；然后再從結論D出發尋找此結論生成必須依賴的命題C1，C2，C3……

如果由B1，B2，B3，…中的某個Bi可以推出C1，C2，C3，…中的某個Ci，則可得到一串命題：A-Bi-Ci-D，則命題得證.

雙向分析的運用中有時只要用到追溯，有時只要用到條件伸展就能夠解決問題，因此，教師引導學生進行雙向分析時不能機械運用.

2.差異分析

條件與結論之間的邏輯關系是雙向分析時所側重的要點，而條件與結論之間的差異則是差異分析法尤其注重的關鍵.

例6 若a、b、c是互不相等的實數，且滿足關系式

b2+c2=2a2+16a+14， ①

bc=a2-4a-5， ②

則a的取值范圍為______.

條件是關于a、b、c的兩個等式，要求的則是關于a的不等式，對比分析可知其差異性表現在以下三個方面：

（1）條件中包含兩個式子，但要求的只是一個，因此立馬可以聯想合并條件；

（2）條件中涉及了三個字母，但要求的只是一個，因此立馬可以聯想消元；

（3）條件中給出的式子是等式，但要求的卻是一個不等式，因此立馬可以聯想到對等式放縮.

解：①-2×②，（b-c）2=24a+24，因b≠c，有（b-c）2＞0，則24a+24＞0，a＞-1.

四、變更問題引導學生再思考

如果對條件與結論進行如此的分析之后還不能求解，那么解題者就應該要考慮到變更問題才行了.變更問題時可以將問題全部變更，也可以將條件或者結論進行單獨的變更.

1.表示形式的轉換

學生對某些問題的表示形式難以理解或難以探究出解題思路時，教師應該適時引導學生將其表示形式作出一定的變換，問題很可能迎刃而解.如求函數的零點個數問題，有部分復雜的方程學生是無法解出的，要將函數變為兩個簡單函數，畫出它們的圖像交點的個數就是零點的個數，初學的學生比較難解決這類數形結合的問題，老師在教學過程中不斷滲透.

例7函數f（x）=lnx+x-2的零點個數為______.

解法：作出函數g（x）=lnx，h（x）=-x+2圖像，由圖3可知f（x）的零點個數為1個.

2.問題轉化

如果轉化為|AB|是x的函數，則此題就由幾何問題轉化成了代數問題.

3.邏輯轉換

數學解題中可以通過原命題的逆命題或否命題的研究并將之與原命題的本質進行聯系來解決問題.

例8 已知以下二次方程：x2+4mx+4m2+2m+3=0；x2+（2m+1）x+m2=0；（m-1）x2+2mx+m-1=0. 其中至少有一個方程有實根，則m的取值范圍為（ ）.

當然在變式的過程中運用的最多的是分類討論思想，當問題比較復雜甚至難以入手時，一般將其轉化成比較簡單且易于解答的一道或幾道新題.

上面一些常用方法，老師在平時的教學中，可經常滲透，讓學生有一個接受，消化的過程，讓他們建立起解題的一套方法和思路，但重要經驗是優化基礎，把知識結構化、系統化、程序化，在優化的基礎上，適當地做一些新題.基礎好了，才能夠做到解題活，才能綜合知識，有較快的解題速度，所以應該把主要精力放在優化解題過程，濃縮提煉知識的機構，優化解題方法.H