學理分析：讓結構化學習深度發生

席愛勇，吳玉國

（1.淮安市工業園區實驗學校，江蘇　淮安　223008；2.淮安市淮陰區教師發展中心，江蘇　淮安　223300）

小學數學結構化學習的學理旨在通過對數學知識結構與學生的認知結構深度分析，融通共生，讓學生經歷數學認知的完整過程，建構數學知識的完整樣態，實現知識技能、過程方法、情感態度、思想價值等多層面數學素養的全面發展。正如圖1所示，學生數學知識結構是由與新知相關的核心元素、課時內容、單元整體、領域分布以及學科之外的廣闊的生活世界共同構成的多維度立體結構。在數學知識結構的建構過程中，通過直觀操作、描述分析、抽象概括、實踐應用等認知結構化加工，最終形成學生的知識技能、過程方法、情感態度、思想價值等多層面數學素養結構。

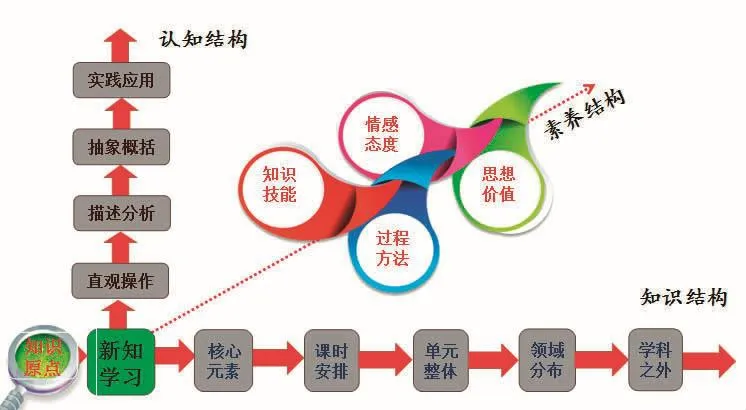
圖1　學生數學知識結構

一、數學知識結構分析

美國認知心理學家布魯納指出：“掌握事物的結構，就是允許許多別的東西與它有意義地聯系起來的方式去理解它。簡單地說，學習結構就是學習事物是怎樣相互關聯的。”[1]小學數學結構化學習著眼于數學整體知識結構的建構，通過對課時內容與本單元、本領域、相關領域和學科外內容的關聯性結構分析，將課時內容置于數學整體知識結構中去建構，使課時內容具有連續性、關聯性和生長性，實現在局部中認識整體，在整體中認知局部。

（一）課時內容的宏觀關聯結構分析

1.課時內容與單元內容的關聯結構分析

如果把課時內容看作一個點，那么單元內容就是一條線。“點動成線，點線相連。”因此教師要厘清課時內容在本單元中的前沿后續，充分認識課時內容在本單元的作用和價值，看到課時遞進的層次和關聯，形成單元整體結構。例如，蘇教版義務教育教科書《數學》五年級上冊第三單元例1“小數的意義”與單元內容關聯性分析（如表1）。

從表1中我們不難發現：例1“小數的意義和讀寫”是整個單元內容的基礎，在整個單元學習中起著統攝作用。在這一課中讓學生直觀而深刻地認識小數的產生、分不足、平均分、分母是10、100、1000……的分數和一位小數、兩位小數和三位小數的關聯對后續學習小數相關內容起到至關重要的作用，后面幾課時的學習內容都是例1學習內容的自然遞進。

2.課時內容與領域內容的關聯結構分析

如果把課時內容和單元內容看作點線關系，那么課時內容與領域內容就可以看作點面關系。在這里，我們不僅要分析課時內容與本領域的關聯，還要分析課時內容和數學相關領域的關聯，用整體關聯的眼光看待課時內容。例如我們在學習“小數的意義和性質”時，不僅要和三年級下冊“小數的初步認識”、五年級上冊“小數的四則運算和混合運算”、五年級下冊“小數和分數的互化”以及六年級上冊“小數和百分數的互化”“求比值”相聯系，還要和三年級上冊的“分數的初步認識（一）”以及三年級下冊的“分數的初步認識（二）”相聯系，以及一至四年級的“整數的意義、讀寫以及大小比較、十進制計數法”等知識相聯系，將小數看作十進制分數系和整數系向細分方向的拓展，這樣就把小數意義和分數、整數有機聯系起來，弄清小數意義知識的前延后續、縱橫聯系，在“數與代數”的領域框架下理解和建構小數的意義。當然，我們也要看到“小數的意義”與“圖形與幾何”“概率與統計”等相關數學領域的普遍聯系。例如我們在學習“小數的意義”時，需要涉及物體長度的丈量、正方形和正方體的分割、人民幣單位換算、長度單位換算等很多“圖形與幾何”領域的知識技能，在平均分、數一數時也涉及“統計與概率”領域的思想方法。

表1　“小數的意義”與單元內容的關聯性分析

3.課時內容與學科外內容的關聯結構分析

我們不僅要看到課時內容與單元內容、領域內容之間的關聯，即學科內的知識結構關聯；還要看到課時內容與學科外其他學科知識結構乃至學生整個生活世界的結構關聯，將課時內容置于學生廣闊的生活世界里來進行結構化學習設計，讓課時內容真正站立起來，不斷豐盈起來。例如，我們在學習“小數的意義”時，不僅要看到它與小數的性質、小數大小比較、小數四則運算等小數領域知識的結構性關聯，還要看到它與分數、整數、比等“數與代數”領域相關知識的結構性關聯以及與“圖形與幾何”“概率與統計”等數學領域的結構性關聯，更要看到它與學科外其他學科如自然、物理、化學等學科結構性關聯，尤其是學生日常生活世界的結構性關聯，如丈量物體長度、貨幣兌換等。

（二）課時內容的微觀元素結構分析

如果說上面是課時內容的向外拓展性結構研究，那么課時內容的元素結構分析就是課時內容的向內微觀性結構研究。通過課時內容的向內微觀性結構研究，即通過課時內容各個教學要點的元素分解與重組，不斷優化課時內容的呈現方式，豐富課時內容的內涵品質，使課時內容更有普適性、深刻性和生長性。如我們在學習“小數的意義”時，可以將課時內容分解為整體認識（如生活經歷、學習經驗）、理解（如丈量、分不足、小數表達）、讀寫（零點幾、幾點幾）、計數單位（如十分之一、0.1、直尺上的分數與小數）、數位（如十分位、小數點、數位順序表等）、進率（如滿十進一、正方形數軸、計數器等）等若干學習要點，再將這些學習要點的落實分解成若干核心要素，對這些核心要素進行再優化組合，從而實現數學學習的“再創造”，不斷提升學習效果和內涵品質。

二、學生數學認知結構分析

美國認知心理學家奧蘇伯爾說:“每當我們致力于影響學生的認知結構，以便最大限度提高意義學習和保持時，我們就深入到了教育過程的核心。”[2]在學生認知結構形成過程中，知識的組織和表征是兩個非常重要的影響因素，教師應該以此為依據，運用合理的教學策略，力爭使學生構建合理的認知結構。

學生數學認知結構到底是怎樣形成的？多元表征認知心理學家依據新雙重編碼理論給出了答案。數學表征特指數學領域中的表征，其本質是數學學習對象的一個替代。數學多元表征從本質上分兩類：一是數學對象的言語化表征，如文字、口頭語言、書面語言、邏輯符號、公式定理等，主要指數學中的“數”；二是數學對象的視覺化表征，如圖形、圖表、數學模型、實物情境、表情、肢體動作等，主要指數學中的“形”。數學多元表征就是基于“數”和“形”形成兩類本質不同的編碼系統：言語編碼系統和心象編碼系統。言語編碼系統專門處理言語碼，表征言語信息。心象編碼系統專門處理心象碼，表征非言語信息。[3]

在加工信息的過程中，言語編碼系統和心象編碼系統既相互獨立又緊密聯系。具體體現在它們之間有三種聯系與加工方式：表征性加工、參照性加工和聯想性加工。[4]表征性加工指一個或兩個系統的最初激活，是外界刺激對內部編碼系統的作用或影響。參照性加工指兩個系統之間的相互激活和參照性聯系，即言語碼可以激活心象碼，心象碼也可以激活言語碼。聯想性加工是指一個編碼系統內部的激活擴散即言語系統中的言語碼可以激活言語系統內部其他的言語碼，而心象系統中的心象碼可以激活心象系統內部其他的心象碼。

從數學多元表征認知結構模型（參見圖2）可以看出，教師將數學學習對象以言語信息（口語、文字、符號）和非言語信息（實物、模型、圖片、活動、情境）形式呈現給學生進行外在表征加工。言語信息通過符號語義分析原理進行加工，形成言語表征，以言語碼形式進入學生的言語表征系統；非言語信息通過結構對應原理進行加工，形成圖像表征，以心象碼形式進入學生的心象表征系統。新編碼在系統內與學生系統內原有的舊編碼進行聯想性加工，實現系統內信息相互轉換，建構意義聯系，形成言語碼組織（命題、圖式、CPFS結構等）和心象碼組織（視空間表征、心智模式等），同時在系統間進行參照性加工，實現系統間信息相互轉譯，建構意義聯系，最終整合成學生的數學認知結構，必要時外化應用于新的數學學習對象。可見，數學多元表征學習的內化過程本質上就是對數學學習對象進行多元理解、多元編碼、轉換轉譯、建立數學認知結構的過程；數學多元表征學習外化的過程本質上就是數學認知結構外顯化、可視化，應用于新的數學學習對象的過程。“外在表征——（感知）——內在表征——（轉換）——認知結構——（應用）——實踐表征”構成了學生數學多元表征學習的認知循環系統。[5]

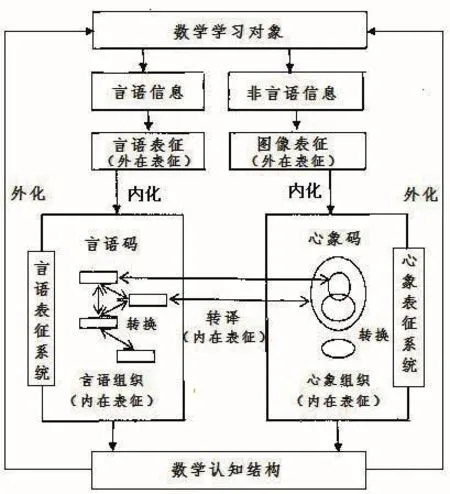
圖2　數學多元表征認知結構模型

三、學生認知結構與數學知識結構融通實踐

小學數學結構化學習以學生數學認知結構發展過程為經線，以數學知識建構過程為緯線，以數學多階思維發展過程為軸線，融通旋轉，形成一個多維度立體式結構化學習方式，讓學生經歷認知發生發展的完整過程，建構數學知識的完整樣態，促進數學思維階梯式循環往復螺旋上升，最終實現數學核心素養的落地生根、持續發展。（模型建構如圖3）

從圖3中我們不難看出，小學生的認知發展從直觀操作開始，連續生活體驗，讓生活現象逐步轉化為學生的認知對象，并逐步建立整體表象；通過表象描述，從零星逐步走向豐富，形成關于概念的各種屬性，創生知識胚胎和載體；通過概念分析，關聯概念元素，逐步去除概念非本質屬性，保留概念本質屬性，實現概念類化；通過概念歸納，將概念本質屬性有機組合起來，抽象出概念定義；通過模型建構，建構數學概念和數學符號的關聯；通過符號表達，實現概念符號化模型建構；最后回歸實踐應用，在實踐應用中不斷檢驗完善數學模型，循環演繹拓展數學知識。隨著學生數學認知不斷推進，數學思維不斷進階，學生的數學知識結構也逐步建構起來了。

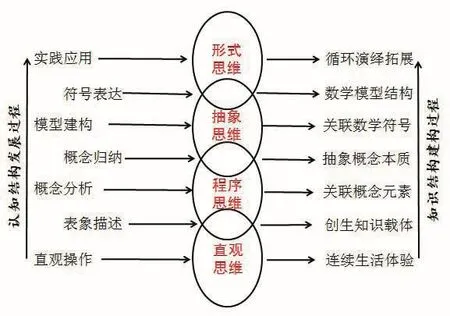
圖3　數學結構化學習模型結構

例如，筆者在教學“小數的意義”時，運用結構化學習模型進行了認知結構發展過程和數學知識結構發展過程實踐分析，并依此進行學程設計，組織課堂教學，學生學得輕松自然、深入淺出，真正實現學一點點，見一片片，從由外而內的結構理解，到由內而外的創生發展。在課堂上，走著走著，教師就“不見了”，學生就成了學習的主人。

因此，小學數學結構化學習在實現學生數學認知結構和數學知識結構以數學思維為軸的自然融通發展中，數學學習自然深度發生，數學核心素養自然落地生根，蓬勃生長。▲

參考文獻：

[1]吳亞萍．“新基礎教育”數學教學改革指導綱要[M].桂林：廣西師范大學出版社，2009:49.

[2]鮑建生，周超.數學學習的心理基礎與過程[M].上海：上海教育出版社，2009:56.

[3][4]唐建嵐.數學多元表征學習及教學[M].南京：南京師范大學出版社，2009:18-39.

[5]席愛勇.多元表征學習：讓數學學習深度發生[J].教學月刊（小學版），2017（7/8）:81-82.