用簡單的方法驗證點電荷概念的相對性

孔　文

（安徽大學江淮學院，安徽　合肥　230031）

點電荷本質上就是帶電體，是一個沒有大小形狀的集合點.而電荷又全部集中在這個幾何點上.事實上，任何帶電體都有大小和形狀，真正地點電荷是不存在的，它像力學中的“質點”概念一樣，純屬一個理想化模型[1].不過，當我們在研究帶電體激發的電場分布及相互作用時，如果帶電體本身的幾何限度比起它們之間的距離小得很多，那么，帶電體的形狀、大小的電荷分布對帶電體之間的相互作用的影響就可以忽略不計.在此情況下，我們仍可以把帶電體抽象成點電荷模型.也只有這樣，“電荷之間的距離”這一概念才有完全的確定的意義[2].故從此角度看，點電荷又是一個相對性概念.為了能對點電荷的相對性認識的更加充分，更加深刻.我們從電偶極子、線帶電體、面帶電體、球帶電體的特殊場點來計算場強分布特點.

1　點電荷電場強度

設在真空中有一個靜止點電荷q，則距為r的P點的電場強度，可由庫倫定律求得.在P點放一試探電荷q0，可知，作用在q0上的電場力是

由（3）可知，點電荷q在真空中任意一點激發的電場強度大小，與點電荷電量成正比，與點電荷到該場點的距離的平方成反比.

2　同性等量點電荷在中垂線上電場強度

設在真空中有兩個等量同性點電荷，電量均為q；q1q2距離21，O為中點，到O的距離為r.

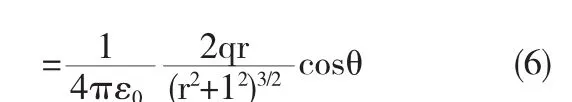
討論，當 r?1，即 limr→∞(r2+12)=r2；limθ→0cosθ=1 可得，

由（7）可見，當P點沿中垂線離開O點的距離比點電荷系本身的大小大的多時，P點的電場強度與一個電量為2q的在O點的點電荷電場強度相等，即驗證了點電荷概念的相對性.完全可以把該模型當做點電荷模型來處理相關問題.

3　有限長線帶電體電場強度

3.1　帶電直導線在延長線上電場強度

設真空中有帶電直導線長1，帶電量Q（均勻帶電），在導線的延長線上電場強度滿足何種分布規律?若滿足一定的條件，線點電荷場強分布模型是否又可轉化為點電荷模型.

P點距導線一段端的距離是d，另一端為O點向右建立x軸坐標系，在導線任意位置取一個點電荷dq，dq到O點的距離是x，則dq在P點的場強

根據電場疊加原理

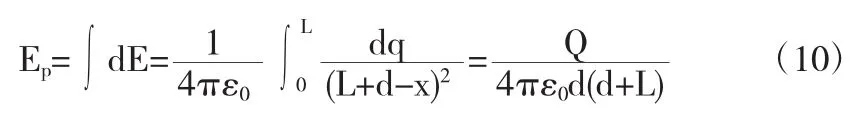
討論，若滿足 d?L，limd→∞d(d+L)2=(d+L)2

由(11)可見，當場點P距導線的一端的距離遠大于導線自身長度時，P點的場強與把所有電量Q集中在O點的一個點電荷在同樣場點的場強相等.驗證了點電荷概念的相對性.完全可以把該模型當做點電荷模型來處理相關問題.

3.2　帶電直導線在中垂線上電場強度

設真空中有帶電直導線長2L，帶電量Q（均勻帶電），O是導線中點，P到O的距離為r.導線的中垂線上電場強度滿足何種分布規律?若滿足一定的條件，該模型模型是否又可轉化為點電荷模型.

由(15)可見，當導線中垂線上場點P距導線的距離遠大于導線自身長度時，P點的場強與把所有電量Q集中在O點的一個點電荷在同樣場點的場強相等.驗證了點電荷概念的相對性.完全可以把該模型當做點電荷模型來處理相關問題.

3.3　帶電圓周導線在軸線上電場強度

設Oyz平面內有一半徑為R的圓環，均勻帶有電量Q，則軸線上任意一點P的電場強度滿足何種分布規律？若滿足一定的條件該模型模型是否又可轉化為點電荷模型.

討論，若 x?R；limx→∞(x2+r2)3/2=x3

由(19)可見，當帶電圓周導線軸線上場點圓心的距離遠大于導線自身長度時，P點的場強與把所有電量Q集中在O點的一個點電荷在同樣場點的場強相等.驗證了點電荷概念的相對性.完全可以把該模型當做點電荷模型來處理相關問題.

4　有限大帶面帶電體電場強度

設Oyz平面內有一半徑為R的圓盤，均勻帶有電量Q，則軸線上任意一點P的電場強度滿足何種分布規律？若滿足一定的條件該模型模型是否又可轉化為點電荷模型.

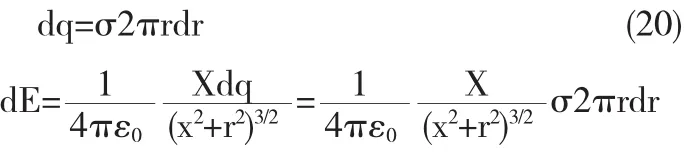
討論，若x?R，利用二項式定理展開

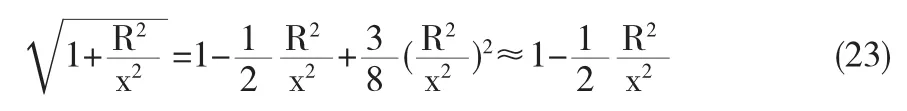
將（23）代入（4-3）Ep=

由(24)可見，當帶電圓盤軸線上場點距圓心的距離遠大于自身大小，P點的場強與把所有電量Q集中在O點的一個點電荷在同樣場點的場強相等.驗證了點電荷概念的相對性.完全可以把該模型當做點電荷模型來處理相關問題[3].

5　帶電球體外場電場強度

設帶電球體均勻帶電電量Q，球體半徑為R，球體外任意一點P的電場強度滿足何種分布規律？

由(26)可見，球體外P點的場強與把所有電量Q集中在圓心點的一個點電荷在同樣場點的場強相等.驗證了點電荷概念的相對性.完全可以把該模型當做點電荷模型來處理相關問題.

6　結束語

通過以上幾個特殊的模型我們不難發現，當場距遠大于帶電體自身的尺寸時，不管帶電體所帶電量有多大，在特殊場點上的電場分布無一例外的都是滿足點電荷電場強度分布.這里值得一提的是，雖然本文所選的模型具有一定的特殊性（所帶電荷對稱分布），所討論的場點也是特殊位置，但是不可否認的是，原則上總可將帶電梯看成是由無數個點電荷元所組成的連續點電荷系.[4]然后在利用適用點電荷相互作用規律的庫倫定律，通過求和或者積分求出電場分布，其結果也可以證明電場分布與源電荷的電量成正比與場距的平方成反比的結論，這個結論另做討論.

參考文獻：

〔1〕孔祥鯤.基于MATLAB構建點電荷系的電勢與電場強度分布圖[J].實驗技術與管理，2007，24（10）.

〔2〕劉耀康.用計算機繪制點電荷對的電場線[J].大學物理，2005，24（8）.

〔3〕程守洙.普通物理學[M].北京：高等教育出版社，2006.

〔4〕韓家華.大學物理學[M].合肥：安徽大學出版社，2009.