基于時間窗約束下的外賣配送路徑優化

翟勁松，臺玉紅　（上海理工大學，上海 200093）

ZHAI Jinsong,TAI Yuhong　(Shanghai University of Science and Technology,Shanghai 200093,China)

0　引言

隨著互聯網的發展以及生活節奏的加快，越來越多的人購買外賣。當下最主流的外賣銷售形式是通過的O2O方式，即消費者線上下單，商家接單后線下送貨上門。由于外賣配送的特殊性，于是配送問題一直是各大商家需要解決的難點，在提供配送服務的過程中，顧客往往約定外賣送達時間，商家需保障外賣的準時送達，一旦外賣未能準時送抵顧客處，顧客滿意度會受到影響，顧客會將不滿信息反饋到外賣平臺以供其他顧客參考，會損傷外賣提供商的品牌效應，對經營業績產生不良影響。因此，以時間窗為約束條件，以配送時間最短為目標，合理高效地組織配送服務對提高商家的自身競爭力具有重要意義。

帶時間窗的車輛路徑問題（Vehicle Routing problem with Time windows，VRPTW）是在VRP的基礎上增加了客戶要求訪問的時間窗口，是VRP的一類重要拓展，可簡單描述為：在不違背車輛限制的條件下，用于送貨的若干車輛從配送中心出發，在返回到配送中心前，以最低的總成本滿足處在不同地理位置的客戶對供貨數量、質量和服務時間的要求。許多與時間相關的運輸調度問題都可歸結為VRPTW，例如郵件的投遞、公交的調度、JIT模式下物料的配送等，根據時間要求合理安排車輛路線是提高服務質量和經濟效益的重要手段。由于VRPTW本身的復雜性以及相應的實踐問題，各國學者進行了大量研究。同時VRPTW屬于NP難問題，一般采用啟發式算法求解，例如節約法[1-2]、遺傳算法、捕食搜索算法[3]。張建強、潘立軍（2012）[4]等都曾利用遺傳算法求解物流配送路徑優化問題。馬韶涵（2016）[5]等將外賣的配送分為了餐飲企業配送模式，外賣平臺配送模式，第三方物流企業配送模式三種方式，并對外賣平臺配送模式進行了研究，對該配送模式存在的問題進行了分析和提出了解決對策。郭月（2016）[6]等通過使用節約里程法對校園外賣配送路徑的優化，從而達到配送的高效率。張弘穎（2014）[7]為了實現熟食運送的快速和經濟合理，采用遺傳算法對配送路徑進行了優化，最后通過實驗驗證該方法是可行的、有效的。王帥（2017）[8]通過遺傳算法有效地計算出響應顧客需求的最優車輛路徑，并分析了顧客完全滿意度區間大小、顧客滿意度敏感性以及配送車輛數量等因素對配送方案總體滿意度水平的影響，最后提出了提高外賣O2O配送滿意度的建議。

1　問題描敘

本文是研究帶有時間窗約束的外賣車輛配送問題，目標是在顧客需求時間約束的情況下，商家的配送總時間最短。通過對周邊的商家進行調研，將本論文的問題進行了簡單的描述，主要可描述為一個商家也是配送中心，所有的訂單都是在配送中心進行處理和分配，之后向周邊多個顧客點進行配送服務，由配送中心的多輛車從配送中心出發，在顧客約定的時間限制下進行配送，最后在配送完之后再返回配送中心的一個過程，如圖1所示：

圖1　一條路徑的配送過程

2　模型建立

2.1　問題假設

在外賣配送過程中，會有出現很多情況，導致配送時間的浪費。（1）配送物損傷，如果配送車輛裝載過多，可能出現貨物被擠壓受損等情況，配送員需要花費時間解決該種情況；（2）配送車輛由于出現一些情況，無法進行配送，導致配送不及時；（3）出現重復配送情況，使得配送效率降低，等等。于是為了避免出現上述的一些情況，本文做出如下的假設：

假設一：在每條送餐路徑上，車載重不小于顧客訂單總需求和。

假設二：每條送餐路徑的配送時間不大于配送車輛的最大行駛時間。

假設三：一個客戶的訂單只能由一輛車進行配送。

2.2　模型參數

對于本論文模型，其中的主要參數如下：

K為商家配送車輛數；

Qk為每輛車的車載量；

Tk為車輛配送的最大行駛時間；

En為顧客訂單要求最早達到時間；

Fn為顧客訂單要求最晚達到時間；

L為配送送貨點個數，其訂單量記為qi（i=1,2,）…；

tij為客戶點i到j的配送時間；

nk為第k輛車配送的顧客配送點數；

Rk表示第k條路徑的集合；

rki表示顧客點rki在路徑k中的順序為i；

令rk0=0表示商家的配送中心。

2.3　模型設立

針對本論文的目標，建立如下的模型：

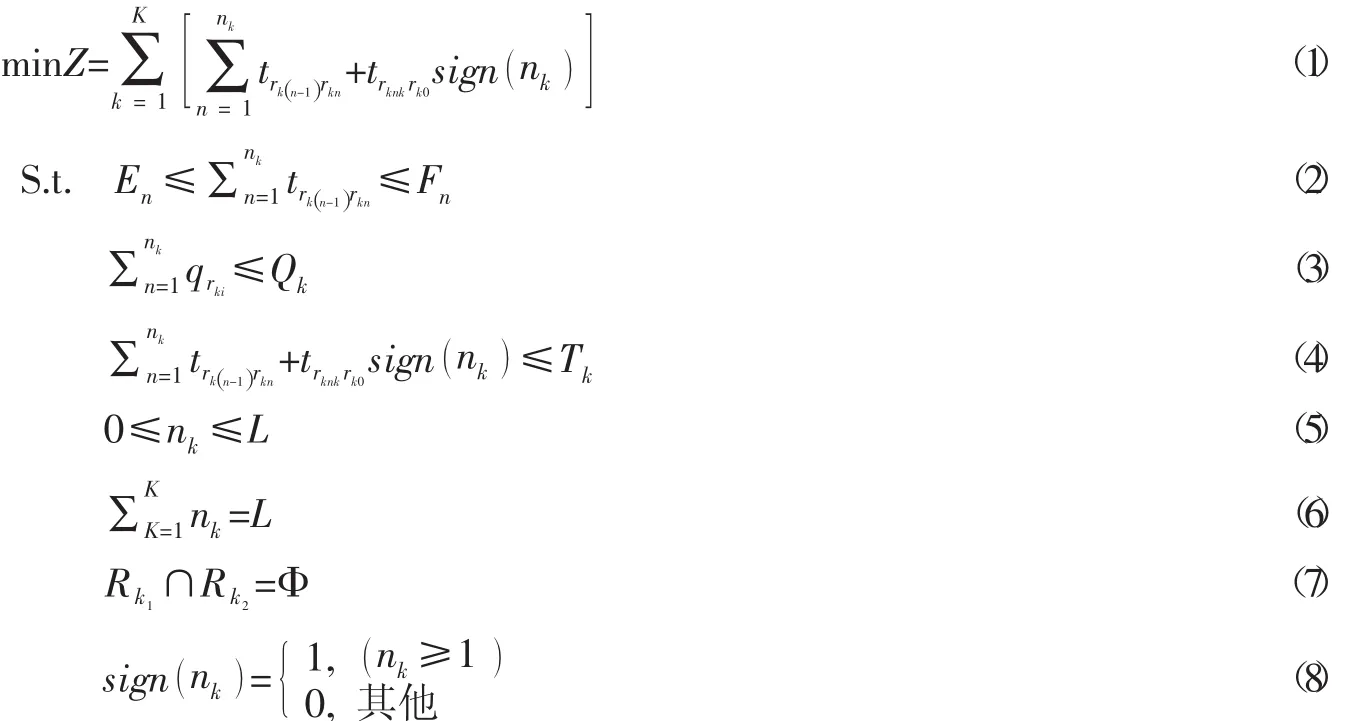
其中：式（1）為目標函數，式（2）確保顧客訂單在顧客規定的時間窗內送到，式（3）確保每條配送路徑上的車載量顧客訂單的總和，式（4）確保每條路徑的配送時間≤配送車輛最大行駛時間，式（5）每條路徑的顧客訂單數≤總的顧客訂單總數，式（6）確保貨物送到每個客戶，式（7）確保每個顧客的訂單由一輛車進行配送，式（8）中的0表示該輛車沒有被使用。

3　算法求解

遺傳算法由美國J.H.Holland教授在20世紀70年代提出。該算法是基于生物進化理論的自適應隨機搜索算法，對于求解路徑優化問題十分有效。路徑優化問題是遺傳算法應用十分成熟的領域，該算法求解路徑優化問題的基本步驟為：編碼操作、產生初始種群、計算適應度函數、遺傳算子（包括選擇、交叉和變異）、終止規則。針對本文中的問題，采用遺傳算法進行求解，生成最優的路徑。

（1）編碼。路徑優化問題的編碼方式分為兩種：路徑表示法和相鄰表示法。本文采用第一種編碼方式。舉例說明：設某商家有9個配送點需要進行配送，其中一個可行閉合路徑為則對應的染色體編碼可表示為1 4 3 7 2 5 8 6 9。

（2）產生初始種群。初始種群是進行遺傳進化操作的第一代種群，由N個個體組成。本文初始種群通過隨機方式生成，將初始種群規模設定為N=30，由此則隨機生成30個個體，每個個體代表了一個初始解，由于暫沒有進行遺傳進化，因此這一代種群中個體適應度值偏低。

（3）計算適應度函數。適應度函數是目標函數在遺傳算法中的反映。在遺傳算法中，適應度值大的個體將有更大概率將優良基因信息傳遞給下一代。本文的目標函數是時間最低，因此本文采用時間的倒數作為適應度函數，個體的適應度值可表示為：Fitness=1/z。

（4）遺傳算子。本文遺傳算子分為三個部分為選擇、交叉和變異，選擇：本文依據種群中不同個體的適應度值采用輪盤賭方式進行選擇，該方案能夠保證適應度高的個體以更大的概率被選中。交叉：在遺傳算法中，新個體的產生主要依靠交叉操作。本文進行交叉操作時，為使子代依舊為可行解，采用部分匹配交叉法（PMX）：對兩個父代隨機產生2個位串交叉點，兩點間為交叉匹配區域，然后基于匹配區域內基因的映射關系重新排列區域外重復基因。舉例如下：

父代染色體

父代1：138|27|4965

父代2：726|45|8139

交叉匹配

匹配1：138|45|4965

匹配2：726|27|8139

子代染色體

子代1：138|45|2967

子代2：546|27|8139

其中：子代1和子代2即為通過部分匹配交叉法獲得的新一代個體。

變異：交叉操作能夠使子代保持父代的優良特性，但也會導致算法過早收斂，陷入局部最優。變異操作能夠彌補這一缺點，擴大遺傳算法的搜索空間。本文采用對換變異法：首先，隨機選擇染色體的兩個基因，然后交換位置，完成對換變異，舉例如下：

變異前：2 3 8 6 7 1 9 5 4

變異后：2 3 9 6 7 1 8 5 4

（5）終止條件設定。遺傳算法本質上是隨機搜索算法，因此難以找到準確的收斂性判別標準。本文采用遺傳算法進化代數作為終止條件。當進化代數達到預先設定值200代時，算法終止，并輸出適應值最大的個體作為最優解。

4　算例分析

本文考慮某個餐廳在某天11:30到12:30時間段內對其9個配送點（編號為1,2,…,9）進行外賣配送服務，各配送點之間的配送時間和到商家的之間的行駛時間如表1，配送點的需求量和客戶需求配送時間窗如表2，商家有三輛配送車，每輛車的最大裝載量為15份，車輛配送的最大行駛時間為120分鐘。

將以上數據帶入模型，經過 Matlab編程進行總時間最小的最優車輛路徑選擇求解運算，可以得到最優配送路徑方案3條（如表3）分別為：路徑1：0-2-1-8-0；路徑2：0-4-9-5-0；路徑3：0-3-7-6-0；最小的配送總時間為93分鐘，平均每條路徑的配送時間為31分鐘。

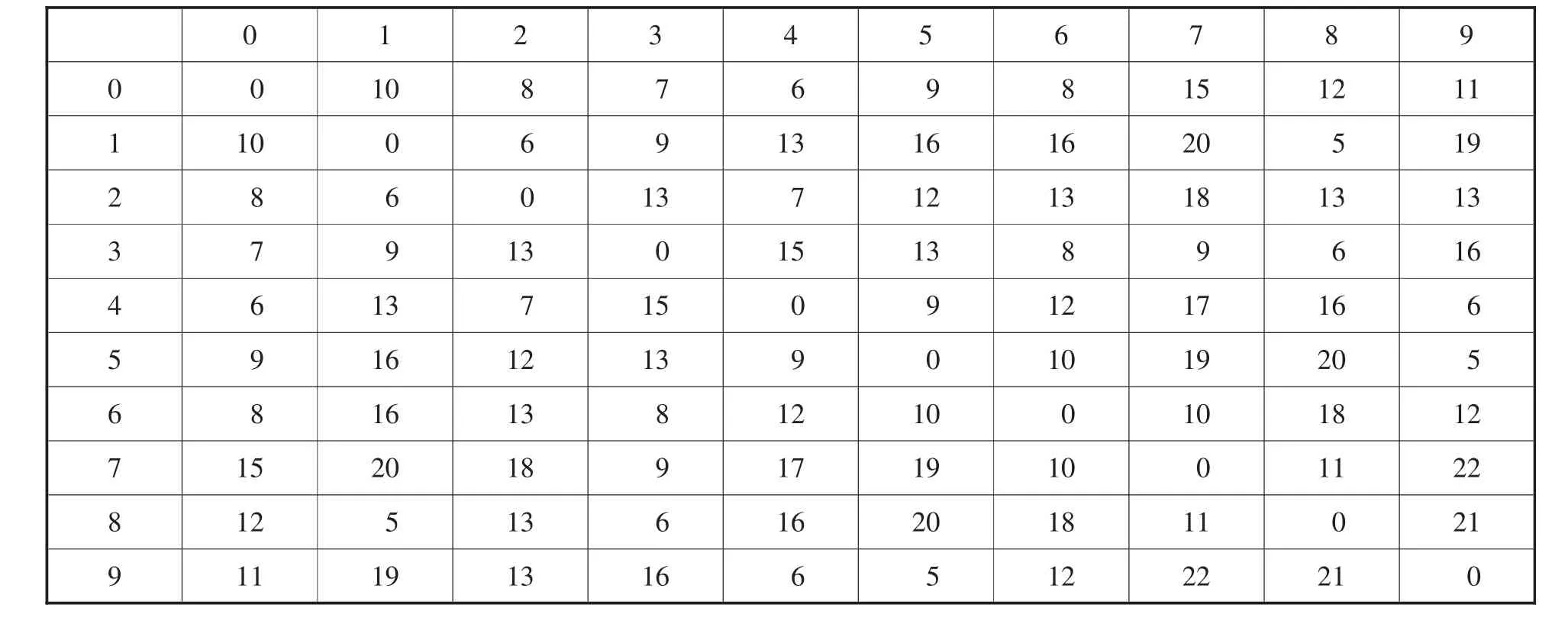
表1　各點之間的行駛時間　單位：分鐘

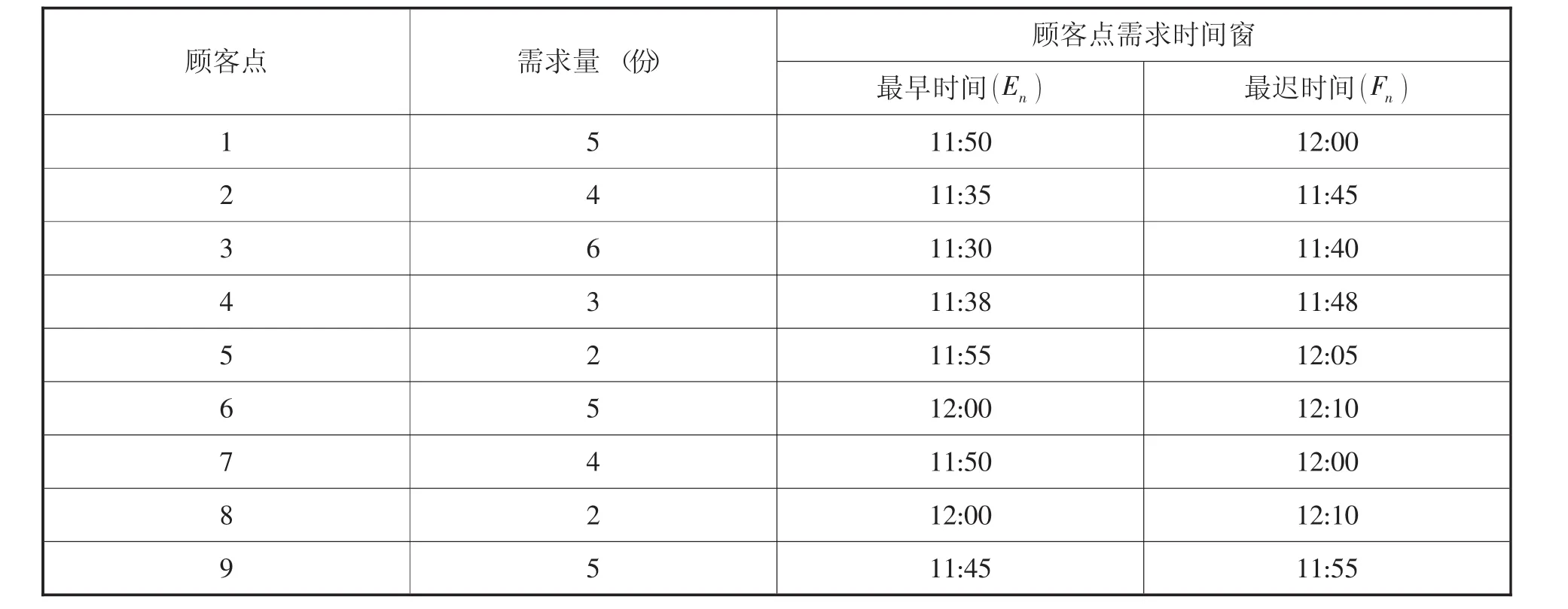
表2　各點的需求量和時間窗

表3　配送最優路徑

5　結束語

隨著人們生活節奏越來越快，顧客對外賣配送時間的要求變得更高。本文通過建立以顧客滿意時間為約束條件，以配送時間最短為目標，運用遺傳算法進行路徑優化，最后通過實例驗證得出該模型可以進行外賣路徑進行優化，即可以滿足客戶對時間的要求，同時還可以減少商家配送時間，提高了商家的競爭力。

參考文獻：

[1] 鄭靜，程幼明.基于時間約束的節約里程法配送路徑優化研究[J].物流工程與管理，2010,32(10):89-90.

[2] 于航，張凱.基于節約里程法的鮮活農產品物流配送車輛路線的最優設計[J].安徽農業科學，2011,39(28):17701-17703.

[3] 蔣忠中，汪定偉.有時間窗車輛路徑問題的捕食搜索算法[J].控制與決策，2007,22(1):59-62.

[4] 潘立軍，符卓.求解帶時間窗取送貨問題的遺傳算法[J].系統工程理論與實踐，2012,32(1):120-126.

[5] 馬韻涵，李品峣.OTO外賣配送分析及對策[J].合作經濟與科技，2016(22):96-98.

[6]郭月，張涵.校園外賣配送體系研究[J].中國市場，2016(20):67-69.

[7] 張弘穎.基于遺傳算法的熟食配送路徑優化[J].科技傳播，2014,6(16):166-167.

[8] 王帥，趙來軍，胡青蜜.隨機旅行時間的外賣O2O配送車輛路徑問題[J].物流科技，2017,40(1):93-101.