古典概型與幾何概型的區別及其求解
幾何概型是與古典概型最為接近的一種概率模型,兩者的共同點是基本事件都是等可能的,不同點是基本事件的個數一個是無限的,一個是有限的。
求解概率問題的關鍵是弄清題中所研究的對象,準確求出試驗與所求事件分別包含的基本事件的個數。
求解幾何概型的概率問題時,首先要準確理解幾何概型的意義,構造出隨機事件對應的幾何圖形與度量區域(長度、面積或體積等),然后利用圖形的幾何度量來求隨機事件的概率。當考查對象為點時,點的活動范圍在線段上,用長度比計算概率;當考查對象為線段時,一般用角度比計算概率;當考查對象在某區域時,用面積比計算概率;當考查對象在某空間時,用體積比計算概率。
一、古典概型
解決古典概型的概率的關鍵是列舉出所有可能的基本事件個數和符合條件的基本事件個數,這些基本事件都是等可能的。
例1某單位欲從包括甲、乙在內的5名應聘者中招聘2人,如果這5名應聘者被錄用的機會均等,則甲、乙2人中至少有1人被錄用的概率是____。
設其他3名應聘者為a,b,c,則從5人中錄用2人的所有可能結果共有10種,列舉如下:(甲,乙), (甲,a),(甲,b),(甲,c),(乙,a),(乙,b), (乙,c),(a,b),(a,c),(b,c)。
其中甲、乙2人至少有1人被錄用的基本事件共有7種情況,列舉如下:(甲,乙), (甲,a),(甲,b),(甲,c),(乙,a),(乙,b), (乙,c)。
例2投擲2枚骸子,則2個點數之和是6的概率為( )。

本題是一個古典概型問題。試驗發生包含的基本事件是同時擲2枚骸子,共有6×6=36(種)等可能結果。而滿足條件的基本事件是2個點數之和是6,共有5種等可能結果,列舉如下:(1,5) (2,4)(3,3)(4,2)(5,1)。
二、與長度有關的幾何概型
求解幾何概型問題的關鍵在于弄清題中的考查對象和對象的活動范圍。若一次試驗中所有可能的結果和某個事件A包含的結果(基本事件)都對應一個長度,如線段長、時間的區間長、距離、路程等,那么需要先求出各自相應的長度,然后運用幾何概型的概率計算公式求出事件A發生的概率。
例3利用計算機產生0~1之間的均勻隨機數a,則事件“3a-1>0”發生的概率為____。
本題是考查幾何概型概率的計算問題。可以將事件“3a-1>0”發生的概率轉化為長度之比。
由3a-1>0,可得在0~ 1中對應的長度為,故所求概率為
例4在區間[0,2]上隨機地取一個數x,則事件發生的概率為( )。

本題是考查幾何概型概率的計算問題。
三、與角度有關的幾何概型
同學們在解答幾何概型問題時,容易混淆幾何度量的比,尤其是角度比與長度比。當題中涉及一個變量時,可以觀察變量可能到達的區域:若變量在線段上移動,則幾何度量是長度;若變量在平面區域(或空間區域)內移動,則幾何度量是面積(或體積)。
需要注意的是:當考查對象為線段時,一般用角度比計算概率;當點的活動范圍在線段上時,一般用長度比計算概率。
例5如圖1,四邊形A B C D為矩形,以A為圓心,1為半徑作圓弧D E交A B于E,在∠D A B內任作射線A P,求射線A P與線段B C有公共點的概率。
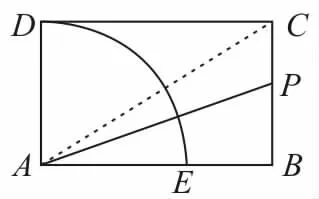
圖1
因為在∠DA B內任作射線A P,則等可能事件為“在∠DA B內作射線A P”,所以它的所有等可能事件所在的區域Ω是∠DA B。當射線A P與線段B C有公共點時,射線A P落在∠C A B內,這時區域d為∠C A B=30°,所以射線A P與線段B C有公共點的概率為
例6如圖2所示,在平面直角坐標系內,射線O T落在60°角的終邊上,任作一條射線O A,則射線O A落在∠x O T內的概率是( )。
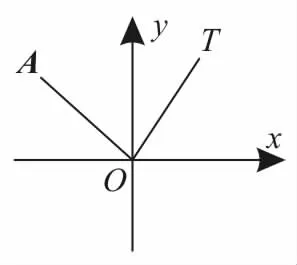
圖2

記“射線O A落在∠x O T內”為事件M,射線O A落在平面直角坐標系內的每個位置的可能性是一樣的。因為周角是360°,∠x O T=60°,所以所求概率
四、與面積有關的幾何概型
與面積有關的幾何概型是近幾年高考的熱點之一,歸納起來常見的命題方向主要是與三角形、矩形、圓等平面圖形的面積有關的問題。當題設條件涉及兩個變量時,一般與面積有關。求解與面積有關的幾何概型時,要注意總的基本事件與所求基本事件分別表示的區域對應的面積。必要時可根據題意構造兩個變量,把變量看成點的坐標,找到試驗全部結果構成的平面圖形,以便求解。
例7甲、乙兩人約定上午9時至12時在某地點見面,并約定任何一個人先到之后等另一個人不超過一個小時,若對方一小時之內不來,則離去。如果他們兩人在9時到12時之間的任何時刻到達約定地點的概率都是相等的,求他們見面的概率。
考慮甲、乙兩人分別到達某地點的時間,在平面直角坐標系內分別用x軸、y軸表示甲、乙到達約定地點的時間,用0時到3時表示9時至12時的時間段,則試驗發生包含的條件是{(x,y)|0<x<3,0<y<3}。
兩人能見面的時間必須滿足|x-y|<1,這就將所求問題化歸為幾何概型問題。
設9時后過了x小時甲到達,9時后過了y小時乙到達,取點Q(x,y),則0<x<3,0<y<3。
兩人能見面所包含的條件是{(x,y)|0<x<3,0<y<3,|x-y|<1|}。作出兩部分對應圖形的區域,如圖3所示。
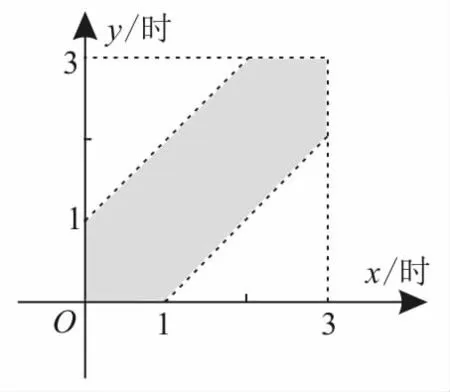
五、與體積有關的幾何概型
對于以體積為度量的幾何概型問題,要根據空間幾何體的體積計算方法,把概率計算轉化為體積計算。解答與體積有關的幾何概型問題時,先分清題目中的條件,找出幾何體的形狀,并計算出總體積,以及所求的事件占有的幾何體的形狀,并計算出體積,然后利用體積之比求出概率。
例8在一球內有一棱長為1的內接正方體,一點在球內運動,則此點落在正方體內部的概率為( )。
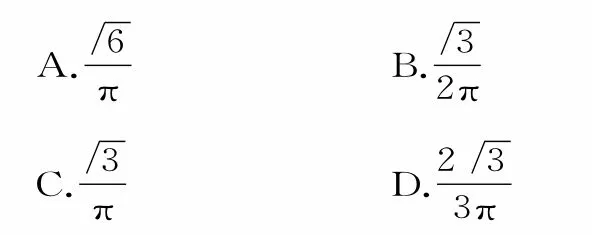
這是一個與體積有關的幾何概型問題。由題意可得正方體的體積為V1=1。又球的直徑是正方體的對角線長,故球的半徑球的體積
六、幾何概型的綜合應用
例9如圖4,在邊長為3m的正方形中隨機撒3000粒豆子,有800粒落到陰影部分,據此估計陰影部分的面積為____ m2。

圖4
根據幾何概型的概率的幾何意義,可得到關于陰影部分面積的等式,解之即可。
由題意可得正方形的面積S1=3×3=9(m2)。
設陰影部分的面積為S2。
因為隨機撒3000粒豆子,有800粒落到陰影部分,所以由幾何概型的概率計算公式可得解得S2=2.4(m2)。
例10已知函數f(x)=2x2-4a x+2b2,若a∈{4,6,8},b∈{3,5,7},則該函數有兩個零點的概率為____。
要使函數f(x)=2x2-4a x+2b2有兩個零點,即方程x2-2a x+b2=0要有兩個實根,則Δ=4a2-4b2≥0,即a≥b。
由a∈{4,6,8},b∈{3,5,7},可知a,b的所有取法共有3×3=9(種),其中滿足a≥b的取法有(4,3),(6,3),(6,5),(8,3),(8,5),(8,7),共6種,所以所求概率為

