概率與統計一家親
有關古典概型與統計相結合的題型是高考考查的一個重要題型,已成為高考命題的熱點,真可謂“概率與統計一家親”。下面舉例說明。
例12016年某電視臺問政直播節目首場內容是“讓交通更順暢”,A,B,C,D四個管理部門的負責人接受問政,分別負責問政A,B,C,D四個管理部門的現場市民代表(每一名代表只參加一個部門的問政)的人數的條形圖如圖1所示。
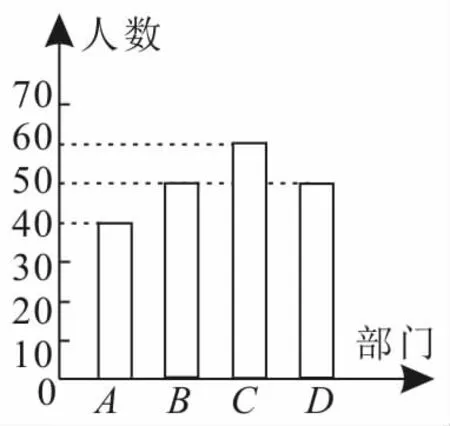
圖1
為了解市民對實施“讓交通更順暢”幾個月來的評價,先對每位現場市民進行了問卷調查,然后用分層抽樣的方法從調查問卷中抽取20份進行統計,統計結果如表1所示。
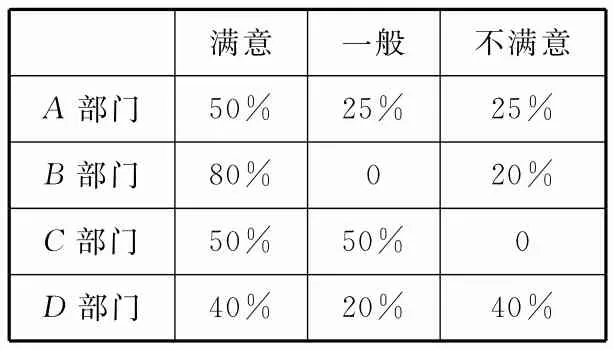
表1
(1)若現場市民甲選擇的是A部門,求甲的調查問卷被選中的概率。
(2)若想從調查問卷被選中且填寫不滿意的現場市民中再選出2人進行電視訪談,求這2人中至少有1人選擇的是D部門的概率。
分析:(1)從圖1中找出分別負責問政A,B,C,D四個管理部門的現場市民代表的人數,便可求出甲的調查問卷被選中的概率。(2)按計算古典概型的三個步驟求解。
解:(1)由圖1可得,分別負責問政A,B,C,D四個管理部門的現場市民代表共有200人,其中負責問政A部門的現場市民為40人。由分層抽樣可得從選擇A部門的調查問卷中抽取了設事件M為“現場市民甲的調查問卷被選中”,所以P(M)=由上述可得,若甲選擇的是A部門,則甲的調查問卷被選中的概率是0.1。
(2)由表1可知,分別負責問政A,B,C,D四個部門的現場市民接受問卷調查的人數為4,5,6,5。其中不滿意的人數分別為1,1,0,2。
記對A部門不滿意的現場市民是a,對B部門不滿意的現場市民是b,對D部門不滿意的現場市民是c,d。設事件N為“從填寫不滿意的現場市民中選出2人,至少有1人選擇的是D部門”。從填寫不滿意的現場市民中選出2人,共有(a,b),(a,c),(a,d), (b,c),(b,d),(c,d),即6個基本事件。而事件N有(a,c),(a,d),(b,c),(b,d),(c,d),即5個基本事件。所以故這2人中至少有1人選擇的是D部門的概率是
例 2為了解學生身高情況,某校以10%的比例對全校700名學生按性別進行分層抽樣調查,測得學生身高情況的統計圖如圖2,3所示。
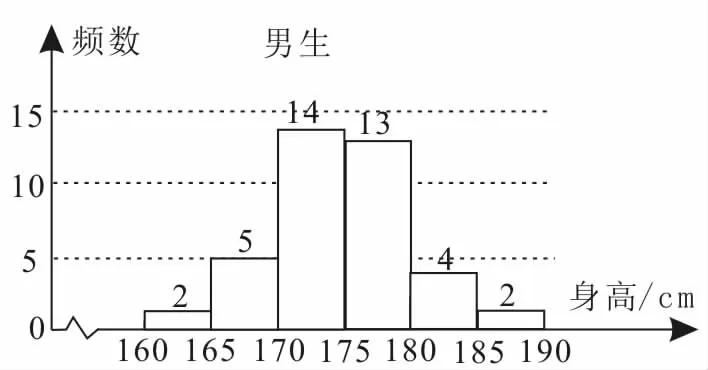
圖2
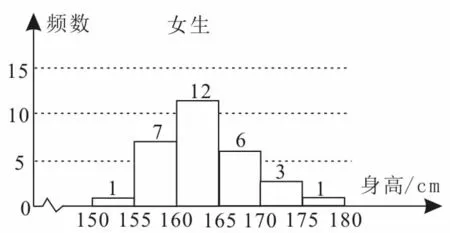
圖3
(1)估計該校男生的人數。
(2)估計該校學生身高在170~185cm之間的概率。
(3)從樣本中身高在180~190cm之間的男生中任選2人,求至少有1人身高在185~190 cm之間的概率。
分析:(1)由樣本中的男生人數可估計該校的男生人數。(2)由統計圖計算該校學生身高在170~185cm之間的頻率。(3)先計算樣本中身高在180~190cm之間的男生人數和樣本中身高在185~190cm之間的男生人數,進而按古典概型的計算方法來求至少有1人身高在185~190cm之間的概率。
解:(1)由圖2和圖3可知,樣本中男生人數為40,女生人數為30,估計全校男生人數為400。
(2)由圖2和圖3知,樣本中身高在170~185 cm之間的學生有14+13+4+3+ 1=35(人),而樣本容量為70,所以樣本中學生身高在170~185cm之間的頻率為0.5。故由頻率估計該校學生身高在170~185 cm之間的概率為0.5。
(3)樣本中身高在180~185cm之間的男生有4人,設其編號為①②③④;樣本中身高在185~190cm之間的男生有2人,設其編號為⑤⑥。從上述6人中任選2人的樹狀圖如圖4所示。
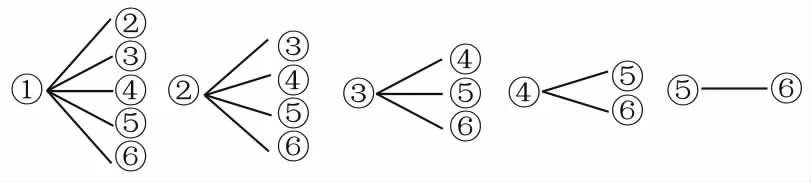
圖4
故從樣本中身高在180~190cm之間的男生中任選2人的所有可能結果數為15,至少有1人身高在185~190cm之間的所有可能結果數為9,因此,所求概率為

