淺談信息技術展示高中數學知識和發展過程的案例研究

廣東省乳源瑤族自治縣高級中學 趙明亮

利用現代信息技術手段可以生動地呈現難度較大的教學內容，對知識的形成和發展可以進行直觀的展現，能夠有效地解決學生在學習中存在的問題，增強學生對數學的學習興趣，提高學生的數學思維及能力；利用信息技術進行數學實驗教學，能促進學生有效探究問題的本質，加深對概念、定理及性質定理的理解；利用信息技術手段，還可以實現學生的學習方式的轉變，促進學生之間的交流與合作，培養學生進行自主合作探究性學習。

一、在信息技術的支持下的數學教學方式發生深刻的變化

使用信息技術進行數學教學，可以為學生創造出圖文并茂、豐富多彩、即時反饋的學習環境。在這樣的環境中，學生對新知識的構建可以在自己觀察、實驗、猜測、推理、交流、反思等過程中完成。信息技術的引入給學生的刺激是多樣性的，既看得見，又聽得著，還可以自己動手操作，這有利于調動學生的積極性和求知欲，對數學知識的獲取和保持具有重要意義，也是數學教學方式與學習方式轉變的具體體現。

案例一.在概率的教學中，書本101頁向我們提出這樣一個問題：取一個邊長為2a的正方形及其內切圓，隨機地向正方形丟一粒豆子，求豆子落在圓內的概率。解決本題其實不難，學生基本都知道所求的概率為圓的面積除于正方形的面積，即然而當老師提出可否用此模型求出π的近似值時，很多學生都懵了。有的學生提出疑問：π的值不是已經知道了嗎，怎么還要估計。少數學生提出假設，如果能算出豆子落在圓內概率為m，那么利用就可以算出π=4m了。那么這時又出現了一個問題：怎么計算豆子落在圓內的概率呢？這時有學生想到做大量的實驗，用頻率估計概率。這的確是一個好想法，但是這個大量的實驗是多少次？這個大量實驗是否會因為人為因素使結果產生偏差呢？而你有這個信心去完成嗎？學生都在交頭接耳地討論怎么做。這時我打開幾何畫板，給學生在電腦中演示這種重復試驗（如圖1）。雖然制作過程有點復雜，但是操作起來非常方便。

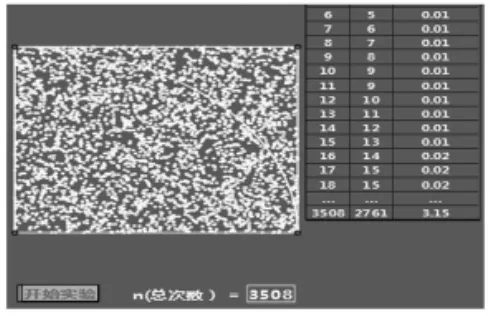
圖（1）

當學生看完演示過程后，都恍然大悟，原來用幾何畫板還能快速地做模擬實驗，而且非常直觀地體現出實驗過程和結果。對于上述思想方法在2017韶關二模文科試題14題中就有所體現。題目是：歷史上有人向畫有內切圓的正方形紙片上丟芝麻來估計圓周率的值，如果隨機地向紙片上撒一把芝麻，1000粒落在正方形上的芝麻有778粒落在正方形的內切圓內，那么通過此模擬實驗計算出π的估計值為____。

二、在信息技術支持下有利于探究知識的發生過程，提高學習效率

信息技術在處理數據上有非常大的優勢，利用excel可以簡化煩瑣的數據處理，讓學生能輕松地解決問題，提高課堂效率，提高學生的興趣。

案例二.《線性回歸方程》的教學

在必修3統計模塊的線性回歸方程教學中，在判斷兩個變量是否具備線性相關關系，要將給出的數據作出散點圖進行判斷。而人工繪制散點圖難度較大，尤其當數據較多和數據以非整數形式出現的時候，人工繪制出的散點圖會產生人為的偏差，課堂不但枯燥，而且費時費力。引入信息技術對數據處理能簡化煩瑣數據帶來的負面影響，而且讓學生操作，可以提高學生的數據處理能力，提高學生的積極性。下面是本節課的部分教學片段。

請同學們看73頁的例題1。下面教同學們利用excel處理數據求線性回歸方程的方法，同學們可以體驗下用excel處理數據帶來的方便。第一步：打開excel表格，將數據分兩行對應輸入到excel表格中，第二步：選中所輸入的數據，點擊“插入”中的圖表按鈕，選擇“xy散點圖”，這樣就呈現出了輸入數據所對應的散點圖。第三步：根據畫出的散點圖判斷出變量具有線性相關關系，接下來利用excel中函數功能，在空白處點擊函數按鈕，在選擇類別中勾出統計，選擇“slope”這個函數，按照提示分別框起y和x對應的數據，點擊確定就出現了a的值，再次選擇統計中的“intercept”這個函數，按照提示再次框起y和x對應的數據，點擊確定就出現了b的值。這時就求出了線性回歸方程了。如圖（2）

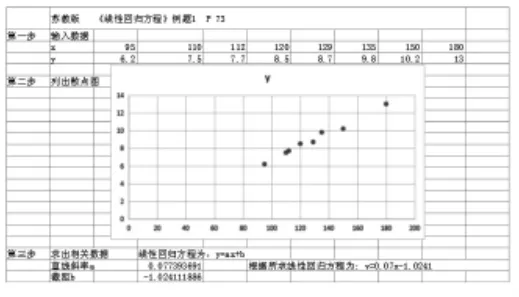
圖（2）

當學生看到利用excel表格三步就能解決所有問題，大家都覺得很神奇。當老師提出有哪位同學想利用excel表格處理75練習第二題的時候，學生都躍躍欲試，最后由鐘文飄和鄭健同學上來展示。展示的情況見圖（3）。從這個教學片段中發現，信息技術的運用，很好地解決了統計中煩瑣數據帶來的問題。信息技術的使用優化了課堂教學，創新了課堂教學模式。通過學生自己的操作，傳統的枯燥的數據處理變成了生動的有趣活動課，提高了學生的學習興趣，也充分體現信息技術支持下的高水平學習過程。

圖（3）

三、借助信息技術探究高考題命制過程

信息技術的引入可以讓我們通過動畫來發現一些結論性的東西，而這些結論也正是命題人命題的方向。通過信息技術可以讓我們探究命題人員對高考題的命題思想和命題過程。

案例三.我們一起來猜想2014年全國甲卷（文）第21題這道題命題人的命題思路。題目是：已知函數f（x）=x3-3x2+ax+2，曲線y=f（x）在點（0，2）處的切線與x軸交點的橫坐標為-2。

（1）求 a。（2）證明：當 k＜1 時，曲線y=f（x）與直線y=kx-2只有一個交點。

我們先來看第一問，命題人以（0，2）這個點來選擇命題是因為這個點是函數y=f（x）圖像與y軸的交點，也是函數圖像唯一的一個定點。那么為什么選擇考查此處的切線呢？我們利用幾何畫板作出函數y=f（x）在（0，2）處的切線。通過動畫我們發現隨著a的變化，函數y=f（x）在（0，2）處的切線也是在變化的，但是當a=1時，切線恰好過點（-2，0），所以命題人就用這個特殊的值進行命題，這時第一問的設問就順理成章了。如圖（4）

圖（4）

對于第二問的設問就更加巧妙，首先我們來思考下為什么命題人會選擇y=kx-2這樣一條直線？其實這條直線不是平白無故出現的，而是命題人通過計算精心設計出來的。首先還是找函數 f（x）=x3-3x2+x+2圖像上特殊的點，我們發現該函數與x軸的交點恰好是（2，0）。通過計算，我們求出函數y=f（x）在x=2處的切線方程為 y=x-2，剛好過（0，-2）。并且發現過（0，-2）向函數y=f（x）圖像作切線巧好只有一條，所以命題人就選擇過定點（0，-2）的直線y=kx-2作為命題基礎。直線y=kx-2已經設出來了，那么試題的考查就應該圍繞參數k來開展，命題的原理還是一樣，通過變化找不變的量。通過變化k值命題人發現：當k＞1時，函數y=kx-2與函數y=f（x）交點的個數是2個或3個，交點的個數不確定會加大命題難度。當k=1時，此時的交點有兩個，此時命題又太過簡單。當k＜1時，通過動畫我們發現兩曲線交點的個數有且只有一個，符合命題要求。題目命完之后當然還要驗證高中生用現有的知識能否解決這個問題。通過論證，第二問的設問學生可以通過已學的知識進行解答，而且體現了數學中一些重要的思想方法，難度適中，完全符合高考題型的要求。如圖（5）

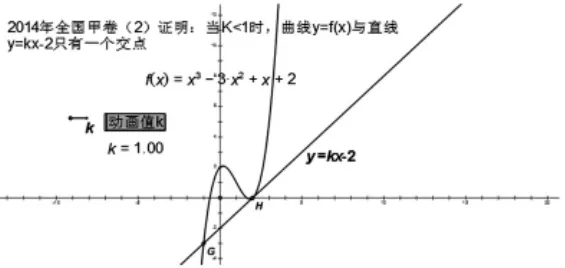
圖（5）

這些案例向我們充分地展示了利用信息技術，可以準確地把握命題人的命題思想和方法，也充分地體現了信息技術在命題過程中起到的作用。信息技術的利用不只局限于解決已知的問題，而是深層次地去發現未知的問題。只有充分地去探索未知世界，才能把信息技術的作用發揮到極致。