圓錐曲線一個定值問題的研究與應用

廣東省東莞市東莞中學 (523005) 于 濤

不少高考試題有著深刻的背景，本文就2017年全國卷Ⅰ理科第10題的命題背景做了進一步的探究，拓寬了圓錐曲線兩條垂直焦點弦長倒數和為定值的成立條件.

一、原題呈現

已知F為拋物線C:y2=4x的焦點，過F作兩條相互垂直的直線l1,l2，直線l1與C交于A,B兩點，直線l2與C交于D,E兩點，則|AB|+|DE|的最小值為( ).

A.16B.14C.12D.10

二、拓展延伸

經過探究發現，除了垂直以外，當兩條焦點弦所在直線關于y=±x對稱時，弦長倒數和也為定值.

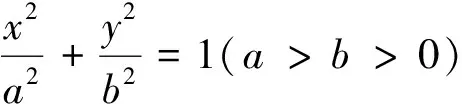
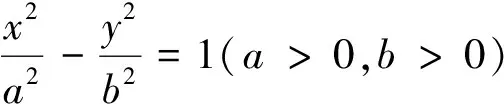
結論2、3的證明可仿照結論1的過程證得，此處不再贅述.需要說明的是，結論2、3中的兩焦點弦可以共焦點，也可不共焦點.

三、結論應用

(Ⅱ)求四邊形ABCD的面積的最小值.

圖1

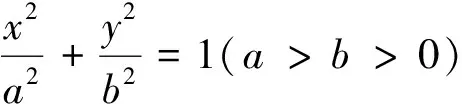
(Ⅰ)求橢圓和雙曲線的標準方程；

(Ⅱ)設直線PF1、PF2的斜率分別為k1、k2，證明：k1·k2=1；

(Ⅲ)是否存在常數λ，使得|AB|+|CD|=

λ|AB|·|CD|恒成立？若存在，求λ的值；若不存在，請說明理由.

在解題時，我們要注重題目背景的挖掘，展開對數學問題的探究，從而發揮試題的價值，提高復習效率.

[1]彭世金.圓錐曲線焦點弦長的一個公式及應用[J]數學通訊，2007(22)：22-23.