永磁同步電動機內置V型轉子結構優化

王 洋，杜欽君，程 祎，張明哲

(山東理工大學 電氣與電子工程學院，山東 淄博 255049)

永磁同步電動機轉子磁路結構不同，電動機的運行性能和控制系統也存在差異. 根據永磁體在轉子上的位置不同，永磁同步電機可分為表面式和內置式. 由于內置式磁路不對稱，有磁阻轉矩產生，且產生相同的輸出轉矩時，較表面式消耗的永磁體要少，經濟效果明顯.單層V型內置式結構，可使勵磁集中，漏磁減少，通過調整V型永磁體的結構和尺寸從而提高電機性能，成為近年來研究的熱點. 文獻[1]對永磁體勵磁角度的改變對氣隙磁場諧波含量的影響進行了研究；文獻[2]通過對五種轉子結構的永磁同步電機進行了有限元分析對比，得出V型永磁體轉子結構的性能特點；文獻[3]基于空載系數和轉矩波動最優化，對通過優化V型永磁體尺寸參數來達到提高電機輸出轉矩和效率進行了研究. 本文研究了內置V型轉子結構永磁同步電動機永磁體張角變化對電機氣隙磁密、齒槽轉矩、電壓諧波畸變率等參數的影響，并采用有限元方法，分析了張角變化過程中電機主要性能參數的變化特點. 為不同設計要求下電機永磁體張角的選取提供了參考依據.

1 電機結構參數對性能參數影響分析

電動機電磁功率[4]為

Pem=mEI

(1)

式中：m為電樞繞組相數；E為每相繞組感應電動勢；I為每相電流.

每相繞組感應電動勢為

E=4kBfW1kwφ0

(2)

式中：kB為氣隙磁場波形系數；f為感應電動勢頻率；W1為每相繞組串聯匝數；kw為繞組系數；φ0為氣隙磁場每極磁通量.

氣隙磁場每極磁通量為

φ0=Bδαiτlef

(3)

式中：Bδ為氣隙磁密最大值；αi為計算極弧系數；τ為極距；lef為鐵心有效長度.

聯立式(1)～(3)可得到電動機電磁功率和氣隙磁密關系為

Pem=4kBmIfW1kwBδαiτlef

(4)

在氣隙磁密為正弦分布時，計算極弧系數αi為常數，電機結構參數一定的情況下，電動機電磁功率僅受氣隙磁密影響，且兩者成線性關系. 在電動機機械損耗和附加損耗一定時，提高電機氣隙磁密可以增大電磁功率，從而提高電動機效率.

2 永磁體張角影響分析

2.1 永磁體張角對氣隙磁密影響

假定不計永磁體漏磁，空載時在考慮到外磁路漏磁導Λσ的情況下，永磁體提供給外磁路總磁通為

φt=φm=-ΛtHmlm

(5)

式中:Λt=Λσ+Λδ, Λt為外磁路總磁導；Λσ為漏磁路磁導；Λδ為氣隙磁導；Λδ和Λσ是并聯關系，有

(6)

且有

(7)

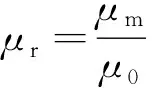
(8)

永磁電機氣隙磁通和氣隙磁密分別為[5]

(9)

將(8)代入(9)并化簡后得氣隙磁密表達式為

(10)

本文以一臺三相12極72槽永磁同步電動機[7]為例進行仿真分析，電機參數見表1，電機轉子各主要參數如圖1所示，取ht、rt為定值，Ds在9～12 mm范圍內變化，Dm的變化范圍為5～7 mm. 通過V型永磁體張角α在100°～130°范圍內的變化對電機主要性能參數的影響進行仿真分析，仿真模型如圖2所示.

表1 仿真電機參數Tab.1 Simulation motor parameters

圖1 V型永磁體轉子各主要參數Fig.1 The main parameters of V-type permanent magnet rotor

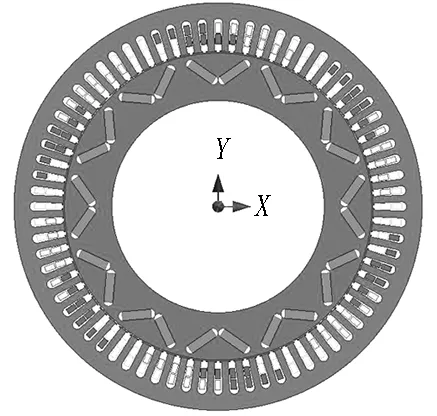
圖2 三相12極72槽電機仿真模型Fig.2 Three phase 12 pole 72 slot motor simulation model

選擇張角為100°、110°、120°、130°對電機進行仿真，得到氣隙磁密波形如圖3所示. 由圖3可知，氣隙磁密由100°到130°變化過程中，氣隙磁密波形沒有出現較大畸變，氣隙磁密幅值和平頂寬度變化明顯，氣隙磁密幅值隨著張角的增大而減小，氣隙磁密平頂寬度隨張角增大而增大.

電機效率的提高在于增大電機氣隙平均磁密，通過近似積分計算，氣隙平均磁密隨張角先增大后減小再增大，在張角為130°時取得最大值，氣隙平均磁密計算值見表2.

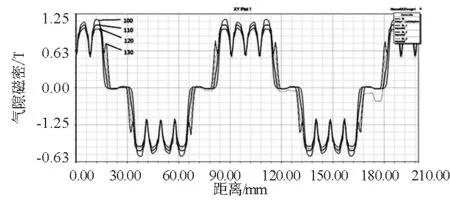
圖3 不同張角下氣隙磁密波形圖Fig.3 Air gap flux density waveform at differnt angles of view

表2 平均氣隙磁密Tab.2 Average air gap flux density

2.2 永磁體張角對感應電動勢的影響

由式(2)、式(3)可得每相繞組感應電動勢為

E=4kBfkwW1Bδαiτlef

在電機結構參數不變情況下，每相繞組感應電動勢隨氣隙磁密Bδ和計算極弧系數αi變化. 由上文分析可知，氣隙平均磁密隨張角先增大后減小再增大，計算極弧系數αi為每極氣隙磁密的平均值與最大值之比，其值也隨張角變化.

表3、表4給出了100°～130°范圍內感應電動勢波形及幅值隨張角變化的情況. 從表3可以看出，感應電動勢波形在100°和105°時正弦特性較差；在110°～125°范圍內，感應電動勢為平滑正弦波，且張角越大，正弦特性越好；在130°時感應電動勢出現諧波畸變，正弦特性變差. 由表4可知，感應電動勢最大值隨張角的增大先增大后減小，且在110°～130°之間變化幅度不大.

通過增大感應電動勢幅值可以提高電磁功率，改善感應電動勢波形可以減少諧波損耗，張角在110°～125°范圍內正弦特性較好，且感應電動勢幅值較大，可以保證電機較高的效率.

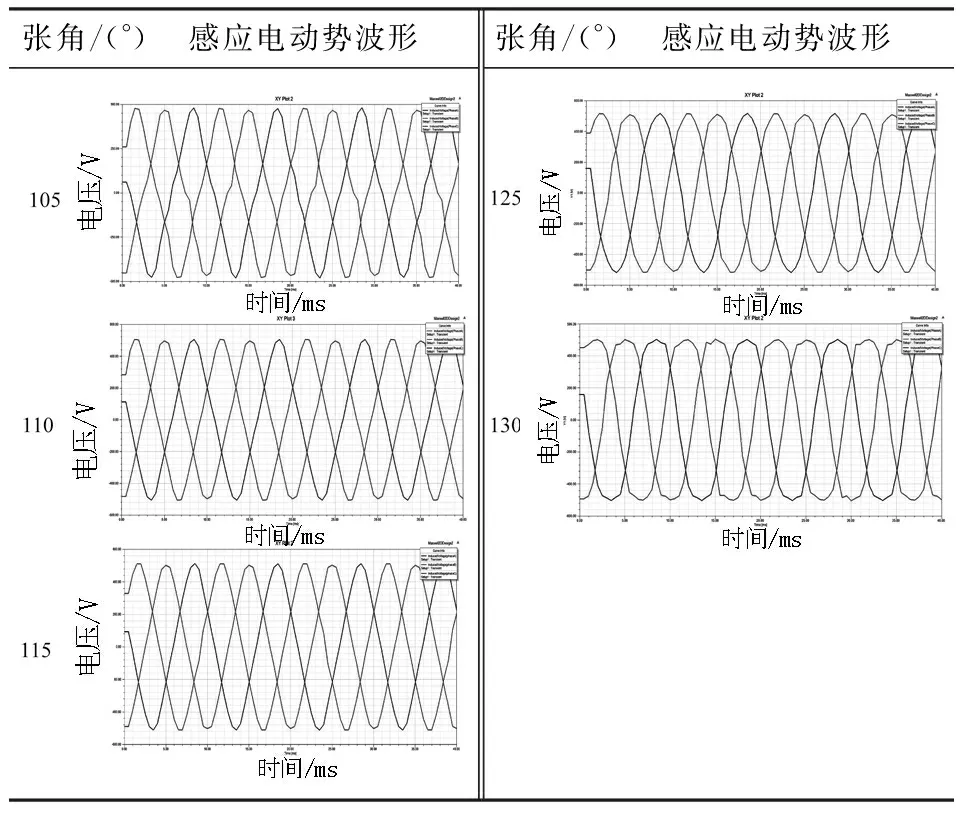
表3 感應電動勢隨張角變化波形Tab.3 Induced EMF with the angle of change

表4 感應電動勢最大值Tab.4 Induced EMF maximum

2.3 永磁體張角對轉矩脈動的影響

2.3.1 永磁體張角對紋波轉矩的影響

紋波轉矩主要由感應電動勢諧波和定子電流諧波相互作用產生. 紋波轉矩與平均轉矩比值為[8]

(11)

式(11)說明紋波轉矩是定、轉子氣隙磁密諧波相互作用的結果. 由于轉子氣隙磁通密度除基波外只有奇次諧波，且三相電機定子氣隙磁通密度沒有3及3的倍數次諧波[9]. 所以，只有定、轉子氣隙磁通密度諧波同為6m±1次時才能產生紋波轉矩，同時，紋波轉矩大小與氣隙磁通密度中對應諧波次數成正比，要減小紋波轉矩，必須盡可能削弱相同諧波相互作用及高次諧波含量.

仿真得到張角為100°、110°、120°、130°時氣隙中的諧波含量如圖4所示. 由于3次、9次諧波僅為轉子氣隙磁通密度諧波，對紋波轉矩沒有影響，本文僅考慮5次、7次、11次諧波的含量的變化. 由圖4可知，5次、7次、9次諧波在100°、110°、130°時含量較少，且沒有明顯變化；在120°時，各諧波含量均明顯增加.

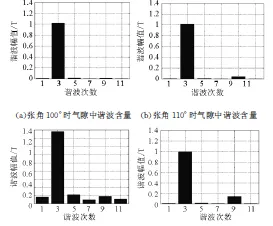
圖4 不同張角時氣隙中各次諧波含量Fig.4 The harmonic contevrt of the air gap under different angles

2.3.2 永磁體張角對齒槽轉矩的影響

齒槽轉矩是永磁電機不通電時轉子永磁體磁場和定子鐵心相互作用產生的轉矩，會影響系統控制精度，引起電機震動和噪聲. 從而由能量法原理可得到電機齒槽轉矩表達式為

(12)

式中：φ為某指定永磁體中心線與定子齒中心線夾角；B為氣隙磁通密度；μ0為真空磁導率.

當電機不存在漏磁和飽和情況時，不同位置氣隙磁通密度可近似表示為

(13)

式中：θ為轉子位置角；Brθ、hmθ和δθ,φ分別為圓周上不同位置的永磁體剩磁感應強度、永磁體厚度和有效氣隙長度.

聯立(12)、(13)式，得

(14)

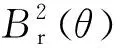
(15)

式中:θso為定子槽口寬對應的弧度值；La為鐵心長度；R2為定子內徑；R1為轉子外徑；αp為極弧系數；p為極對數.

由(15)式可知，在電機主要尺寸、鐵心長度La、定子槽數z、極對數p及永磁體材料和尺寸一定的情況下，電機齒槽轉矩僅受極弧系數αp的影響，且為正弦關系.對于內置式永磁同步電動機，極弧系數=每極永磁體所跨槽數/每極槽數，隨著永磁體張角增大，每極永磁體所跨槽數增加，極弧系數也隨之增大. 不同張角下齒槽轉矩波形及峰值見圖5和表5.由圖5和表5可知，張角在100°～130°變化時，齒槽轉矩先增大后減小，且波動較大，在張角為120°時，齒槽轉矩取得最大值，在130°取得最小值.

圖5 不同張角下齒槽轉矩波形Fig.5 Cogging torque waveform under different angle of view

表5 不同張角下齒槽轉矩的峰值Tab.5 Cogging torque peaks at different angles

3 結束語

通過分析內置式永磁同步電動機永磁體張角對氣隙磁密、電磁功率及轉矩脈動的影響，結合Ansoft maxwell建立仿真模型進行仿真分析，優化永磁體張角有效降低轉矩脈動，減小電壓諧波畸變，增大氣隙磁密.各參數在最優時對應張角不同，根據電機設計要求，適當選取張角，以提高電機性能.

[1]WANG A M, JIA Y H, SOONG W L.Comparison of five topologies for an interior permanent-magnet machine for a hybrid electric vehicle[J].IEEE Transactions on Magnetics,2011,47(5):3 607-3 608.

[2]王艾萌. 新能源汽車新興電機的設計及弱磁控制[M]. 北京:機械工業出版社,2013.75-104.

[3]王艾萌,盧偉甫. 五種拓撲結構的永磁同步電機性能分析與比較研究[J]. 微特電機,2010,38(4):33-37.

[4]宋志環. 永磁同步電動機電磁振動噪聲源識別技術的研究[D].沈陽:沈陽工業大學,2010.

[5]郭培.異步起動永磁同步電機的研究[D].杭州:浙江大學,2013.

[6]王艾萌. 內置式永磁同步電動機的優化設計及弱磁控制研究[D].保定:華北電力大學,2010.

[7]王秀和. 永磁電機[M]. 北京:中國電力出版社,2007.68-70.

[8]馮垚徑. 永磁同步電動機設計關鍵技術與方法研究[D]. 武漢:華中科技大學,2012.

[9]譚建成. 永磁無刷直流電機技術[M]. 北京:機械工業出版社,2014.