《等比數列》教學設計第1課時
(陜西師范大學錦園中學 陜西西安 710016)
一、教材分析
本節課是北師大版《必修5》第一章第三節第一課時,是在學生已經系統地學習了等差數列的概念、通項公式和前n項和公式的基礎上學習。等比數列的定義與通項公式不僅是本章的重點和難點,也是高中階段培養學生邏輯推理的重要載體之一。
二、學情分析
學生已經系統地學習了等差數列的概念、通項公式和前n項和公式的基礎上開始學習,學生有了一定的學習數列的知識基礎,積累了一定的學習數列的經驗和方法,學生較容易通過類比等差數列的學習方法掌握等比數列的定義及通項公式。同時高中學生有一定的觀察、歸納能力、類比聯想能力等,為學生學習等比數列打下了良好的能力基礎。
三、教學目標:
1.知識與技能:理解并掌握等比數列的定義和通項公式,能用定義判斷一個數列是否為等比數列,能推導等比數列的通項公式,能利用通項公式解決相關簡單問題。
2.過程與方法:通過概念、公式和例題的學習,滲透類比思想、方程思想、分類討論思想以及從特殊到—般等數學思想,著重培養學生觀察、比較、概括、歸納、演繹推理等方面的思維能力,并進—步培養分析問題和解決問題的能力,增強應用意識。
3.情感態度與價值觀:培養學生認識和體會類比思想在研究新事物性質中的作用,了解知識間存在的共同規律。
四、教學重點和難點
1.重點:等比數列的概念的形成與深化;等比數列通項公式的推導及應用。
2.難點:等比數列的推導。
五、教法和學法
本節課遵循“教為主導,學為主體,練為主線”的教育思想,輔以多媒體手段,采用學生自主探究的教學方法。本節課設計了 ①創設情境,引入概念②觀察歸納,形成概念③討論交流,推導公式④即時訓練,鞏固新知⑤課堂小結,提高認識⑥作業布置,自我檢測,六個環節,節節相扣,層層深入,從而順利完成教學目標。
六、教學過程
1.復習舊知:(1)等差數列的定義;(2)等差數列的通項公式。
2.新課教學
(1)創設情境,引入概念
引例1:拉面問題(用多媒體展示拉面師傅拉面過程的視頻)
拉面館的師傅將一根很粗的面條,拉伸、捏合、再拉伸、再捏合,如此反復幾次,就拉成了許多根細面條。這樣捏合8次可以拉出多少根面條?前8次拉的面條根數構成了一個列數:1,2,4,8,16,32,64,128 ...①
引例2:《莊子·天下篇》曰:“一尺之棰,日取其半,萬世不竭.”如果將“一尺之棰”視為一份,則每日剩下的部分構成一個數列依次為:
引例3:某轎車的售價約10萬元,年折舊率約為15%,那么該車從購買當年算起,逐年的價值依次為:
請同學們觀察:以上每個數列每一項與前一項之間有什么關系? 這三個數列有什么共同特點?由此引入新課--等比數列。
設計意圖:由生活中的實例,激發學生學習興趣,通過觀察、類比等差數列的定義,讓學生自行歸納總結出等比數列的定義,同時讓學生感受數學就在身邊。
(2)觀察歸納,形成概念
①等比數列的定義:
文字語言:一般地,一個數列從第2項起,每一項與它的前一項的比都等于同一個常數,這個數列就叫做等比數列。這個常數叫做等比數列的公比,通常用字母
符號語言:
②請找出關鍵詞,并思考等差數列和等比數列定義之間有什么聯系和區別?由“差”變“比”會帶來哪些變化了?
注意:
例題1(抓本質,理解概念)試判斷下列數列是不是等比數列,如果是求出公比,若不是說明原因。
① 1,2, 4, 16, 64, …
② 9, 3, 1, 0 ,…
③ 1, -1, 1, -1,…
④ 4, 4, 4, 4 …
⑤ a, a, a, a …
(3)討論交流,推導公式:學生分組討論、交流,上黑板講解。
回顧等差數列通項公式的推導方法:不完全歸納法;累加法;迭代法。類比等差數列推導方法,思考如何推導等比數列通項公式?
方法1:不完全歸納法; 方法2:累乘法;方法3:迭代法。
①等比數列的通項公式
等比數列的首項為公比為等比數列的通項公式為:
②等比數列有什么關系?
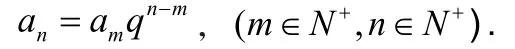
注意:
注意通項公式中四個量“知3求1”的方程思想。
(4)即時訓練,鞏固新知
練習1.求上面三個引例的通項公式:
(3)已知試問48是不是數列中的項,若是,是第幾項?
思考題:在243和3中間插入3個數,使這5個數成等比數列,求這3個數。
(5)課堂小結,提高認識:①知識方面:等比數列的定義,其通項公式及推廣公式的推導,等比數列及通項公式的簡單應用。
②思想方法方面:歸納類比思想,分類討論思想,方程思想,由特殊到一般等數學思想方法。
(6)作業布置,自我檢測
必做題:在等比數列中,設公比為
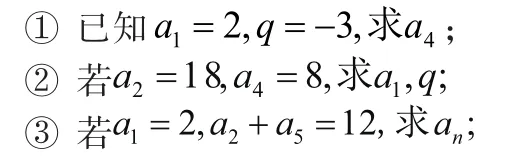
④若a5?a1=1 5,a4?a2=6,求a5.
選做題:在和之間插入三個數,使這五個數成等比數列,則插入的三個數的乘積為多少?
思考題:有四個數,其中前三個數成等差數列,后三個數成等比數列,并且第一個數與第四個數的和是16,第二個數與第三個數的和是12,求這四個數。
七、教學設計反思
本節課采用“讀、說、講、評、議”的方式有意識地讓學生充分地參與等比數列的定義的生成和通項公式的推導到簡單應用,引導學生主動地去觀察歸納、類比聯想,積極地動手、動口、動腦,使學生在學知識的同時形成方法,充分體現了學生是課堂中學習的主體,教師是主導。同時本節課培養學生了觀察、歸納、類比、聯想能力,演繹推理能力,滲透了歸納類比思想,分類討論,方程思想,由特殊到一般等數學思想方法,達到了預期的教學效果。

