圖像預處理討論研究
季祥 劉哲 高超 王浩鑫 武凱璇
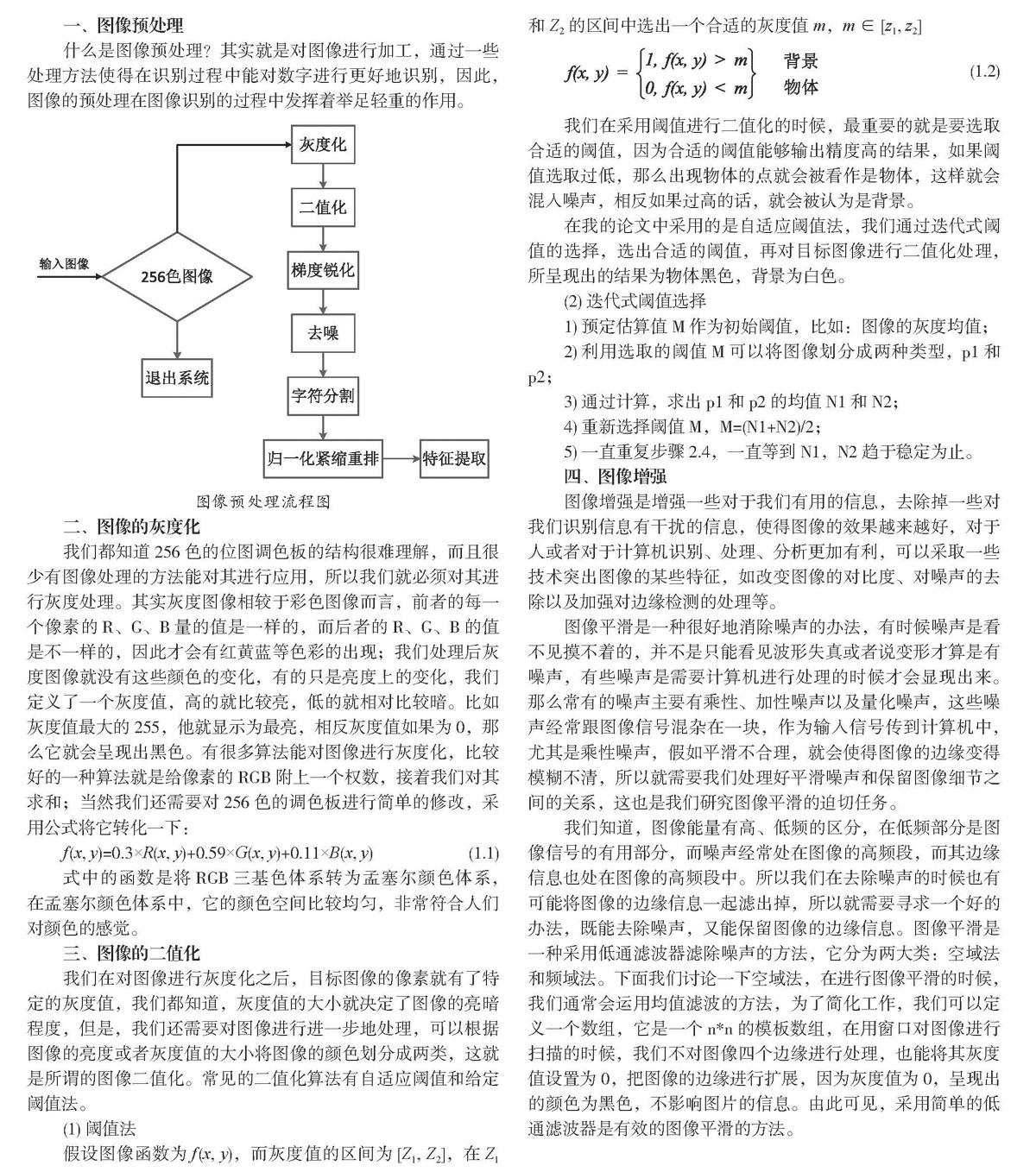

一、圖像預處理
什么是圖像預處理?其實就是對圖像進行加工,通過一些處理方法使得在識別過程中能對數字進行更好地識別,因此,圖像的預處理在圖像識別的過程中發揮著舉足輕重的作用。
二、圖像的灰度化
我們都知道256色的位圖調色板的結構很難理解,而且很少有圖像處理的方法能對其進行應用,所以我們就必須對其進行灰度處理。其實灰度圖像相較于彩色圖像而言,前者的每一個像素的R、G、B量的值是一樣的,而后者的R、G、B的值是不一樣的,因此才會有紅黃藍等色彩的出現;我們處理后灰度圖像就沒有這些顏色的變化,有的只是亮度上的變化,我們定義了一個灰度值,高的就比較亮,低的就相對比較暗。比如灰度值最大的255,他就顯示為最亮,相反灰度值如果為0,那么它就會呈現出黑色。有很多算法能對圖像進行灰度化,比較好的一種算法就是給像素的RGB附上一個權數,接著我們對其求和;當然我們還需要對256色的調色板進行簡單的修改,采用公式將它轉化一下:
f(x, y)=0.3×R(x, y)+0.59×G(x, y)+0.11×B(x, y)(1.1)
式中的函數是將RGB三基色體系轉為孟塞爾顏色體系,在孟塞爾顏色體系中,它的顏色空間比較均勻,非常符合人們對顏色的感覺。
三、圖像的二值化
我們在對圖像進行灰度化之后,目標圖像的像素就有了特定的灰度值,我們都知道,灰度值的大小就決定了圖像的亮暗程度,但是,我們還需要對圖像進行進一步地處理,可以根據圖像的亮度或者灰度值的大小將圖像的顏色劃分成兩類,這就是所謂的圖像二值化。常見的二值化算法有自適應閾值和給定閾值法。
(1)閾值法
假設圖像函數為f(x, y),而灰度值的區間為[Z1, Z2],在Z1和Z2的區間中選出一個合適的灰度值m,m∈[z1, z2]
(1.2)
我們在采用閾值進行二值化的時候,最重要的就是要選取合適的閾值,因為合適的閾值能夠輸出精度高的結果,如果閾值選取過低,那么出現物體的點就會被看作是物體,這樣就會混入噪聲,相反如果過高的話,就會被認為是背景。
在我的論文中采用的是自適應閾值法,我們通過迭代式閾值的選擇,選出合適的閾值,再對目標圖像進行二值化處理,所呈現出的結果為物體黑色,背景為白色。
(2)迭代式閾值選擇
1)預定估算值M作為初始閾值,比如:圖像的灰度均值;
2)利用選取的閾值M可以將圖像劃分成兩種類型,p1和p2;
3)通過計算,求出p1和p2的均值N1和N2;
4)重新選擇閾值M,M=(N1+N2)/2;
5)一直重復步驟2.4,一直等到N1,N2趨于穩定為止。
四、圖像增強
圖像增強是增強一些對于我們有用的信息,去除掉一些對我們識別信息有干擾的信息,使得圖像的效果越來越好,對于人或者對于計算機識別、處理、分析更加有利,可以采取一些技術突出圖像的某些特征,如改變圖像的對比度、對噪聲的去除以及加強對邊緣檢測的處理等。
圖像平滑是一種很好地消除噪聲的辦法,有時候噪聲是看不見摸不著的,并不是只能看見波形失真或者說變形才算是有噪聲,有些噪聲是需要計算機進行處理的時候才會顯現出來。那么常有的噪聲主要有乘性、加性噪聲以及量化噪聲,這些噪聲經常跟圖像信號混雜在一塊,作為輸入信號傳到計算機中,尤其是乘性噪聲,假如平滑不合理,就會使得圖像的邊緣變得模糊不清,所以就需要我們處理好平滑噪聲和保留圖像細節之間的關系,這也是我們研究圖像平滑的迫切任務。
我們知道,圖像能量有高、低頻的區分,在低頻部分是圖像信號的有用部分,而噪聲經常處在圖像的高頻段,而其邊緣信息也處在圖像的高頻段中。所以我們在去除噪聲的時候也有可能將圖像的邊緣信息一起濾出掉,所以就需要尋求一個好的辦法,既能去除噪聲,又能保留圖像的邊緣信息。圖像平滑是一種采用低通濾波器濾除噪聲的方法,它分為兩大類:空域法和頻域法。下面我們討論一下空域法,在進行圖像平滑的時候,我們通常會運用均值濾波的方法,為了簡化工作,我們可以定義一個數組,它是一個n*n的模板數組,在用窗口對圖像進行掃描的時候,我們不對圖像四個邊緣進行處理,也能將其灰度值設置為0,把圖像的邊緣進行擴展,因為灰度值為0,呈現出的顏色為黑色,不影響圖片的信息。由此可見,采用簡單的低通濾波器是有效的圖像平滑的方法。
五、圖像的銳化
在前期的圖像預處理中,有可能圖像會變得模糊不清,使得識別的結果受到嚴重的影響,所以我們需要采取圖像的銳化,提高圖像的清晰程度。我們在對圖像進行處理的時候,時常會對其求平均或者是進行積分運算,這樣的話圖像的高頻分量就會被衰減,對此,我們可以對圖像進行高通濾波,但是噪聲也處在高頻段,在對圖像進行銳化以后,圖像的清晰度增強了,可是噪聲也隨著增強了。所以,在進行圖像銳化的時候,我們要先去除噪聲在對圖像進行銳化處理。我們可以仿造前面圖像增強的方法,采用高通濾波器來實現,只是我們選取的卷積模板不一樣,通常有:
(拉普拉斯模板) 等
除了使用高通濾波器法外,對于圖像的銳化,還有一種比較實用的方法:微分法。在論文里面,我也采用了微分銳化法即Roberts梯度算子,但這種算法能夠去除噪聲,也會對圖像的邊緣有所損傷。
假設原始圖像上的點f(x, y),我們定義f(x, y)在f(x, y)處的梯度矢量為:
G[f(i, j)]=| f(i, j)-f(i+1, j)|+| f(i, j)-f(i, j+1)|(1.3)
我們設定一個閾值Δ進行判定,定義g(x, y)為變化后圖像的函數:
(1.4)
作者簡介:季祥、劉哲、高超:空軍工程大學無線電通信專業;王浩鑫:空軍工程大學通信工程專業;武凱璇:導航工程專業。

