求解矩陣補全問題的三分解方法

，(山東科技大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院，山東 青島 266590)

近年來，矩陣補全問題廣泛應(yīng)用于圖像處理、計算機視覺、數(shù)據(jù)挖掘、模式識別和機器學(xué)習(xí)等領(lǐng)域。作為信號與圖像處理技術(shù)的一個強大的新興分支，矩陣補全已成為繼壓縮感知之后的又一種重要的信號獲取工具[1]。

一般來說，要根據(jù)信號的部分采樣元素來精確地恢復(fù)出所有元素是非常困難甚至是不可能的。但是當(dāng)信號在一組基下是稀疏的且滿足一定條件時，壓縮感知理論證實了可以通過求解l1最小化問題來精確地恢復(fù)所有元素[2]。類似的，當(dāng)信號用矩陣形式表示時，要根據(jù)其部分元素來恢復(fù)所有丟失元素也是很困難的。針對這一問題，Candès等[3]證明了當(dāng)矩陣的奇異值具有稀疏性且采樣數(shù)目滿足一定條件時，大多數(shù)矩陣可以通過求解核范數(shù)最小化問題來精確地恢復(fù)所有元素。由矩陣的部分元素恢復(fù)所有元素這一問題稱為矩陣補全問題，著名的Netflix問題便是一個典型的矩陣補全問題[4]。

給定不完整的低秩缺失矩陣W∈Rm×n，矩陣補全問題可以描述為如下優(yōu)化問題：

(1)

其中A∈Rm×n為待補全的矩陣，Ω是A的p個已知元素的指標(biāo)集。由于秩函數(shù)的非凸性和不連續(xù)性，上述秩函數(shù)最小化問題是NP難的，現(xiàn)有的算法無法有效地解決秩最小化問題。基于此，Candès等[5]證明了可用秩函數(shù)的凸包絡(luò)—核范數(shù)來近似秩函數(shù)，即可將問題(1)凸松弛為如下核范數(shù)最優(yōu)化問題

(2)

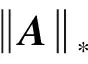
需要指出的是，矩陣補全模型(2)只能對缺失的元素進行恢復(fù)，而無法估計其所含的噪聲。然而在某些情況下，噪聲里往往會包含一些重要的信息，因此，噪聲有時也是非常重要的待恢復(fù)成分。另一方面，矩陣補全模型(2)對大的稀疏噪聲或野點非常敏感，為了克服上述模型的不足，Shi等[6]將矩陣補全模型(2)與魯棒主成分分析(robust principal component analysis, RPCA)模型進行了推廣，提出如下不完全RPCA(IRPCA)模型

(3)

(4)

現(xiàn)有的求解基于核范數(shù)的矩陣秩最小化問題的大多數(shù)算法，每一步迭代都需要進行奇異值分解，而多步奇異值分解則大大增加了算法的計算復(fù)雜度。為了降低計算復(fù)雜度，Xu等[8]將非負矩陣分解算法和矩陣補全模型相結(jié)合，提出了基于非負矩陣分解的矩陣補全模型；Zheng等[9]提出將含有噪聲的低秩矩陣近似問題等價為雙線性分解問題；Shang等[7]則將矩陣雙分解(robust bilinear factorization，RBF)方法應(yīng)用于RMC模型，得到了較好的數(shù)值結(jié)果。

基于矩陣分解在求解基于核范數(shù)的矩陣秩最小化問題中的優(yōu)勢，將矩陣的三分解[10]技術(shù)應(yīng)用到RMC模型中，利用增廣拉格朗日乘子法對模型進行求解，并將新模型應(yīng)用于人臉識別的實際問題。數(shù)值實驗結(jié)果顯示，本研究提出的模型相較于RMC和RBF模型，計算速度更快，實驗效果更好。

1 三分解技巧與模型

在高維數(shù)據(jù)分析中，矩陣分解是一個常用的技巧，也是一個非常有效的工具。常用的矩陣分解主要有QR分解、LU分解、奇異值分解、非負矩陣分解等。現(xiàn)有的大多數(shù)矩陣分解技巧都是將矩陣分解為兩個具有某種特殊性質(zhì)矩陣的乘積。本研究將利用矩陣的三分解技巧及核范數(shù)的正交不變性，盡可能地降低RMC模型的規(guī)模，以達到減少計算量的目的。

下面對所采用的矩陣三分解方法(TFM)進行介紹。設(shè)A∈Rm×n，rank(A)=r，則由參考文獻[10]知，存在矩陣X∈Rm×r，Y∈Rr×r，Z∈Rr×n，使A=XYZT。其中X，Z為具有正交規(guī)范列的矩陣，即XTX=Ir，ZTZ=Ir。

上述分解稱為矩陣A的三分解。本文就是基于矩陣三分解理論對RMC模型(4)進行修改。

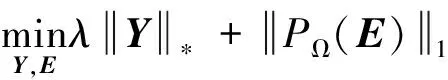
(5)

由矩陣三分解的定義可知，當(dāng)矩陣A的秩較小時，通過矩陣的三分解可將問題的規(guī)模大大降低。將主要針對上述等價模型(5)進行求解和分析。

2 模型求解與算法

本節(jié)中，將利用交替方向乘子法(alternating direction multiplier method, ADMM)對TFMC模型進行求解。

模型(5)的増廣拉格朗日函數(shù)為

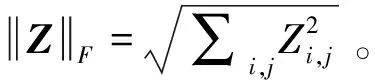
交替方向乘子法的基本迭代公式如下

(6-1)

(6-2)

(6-3)

(6-4)

(6-5)

2.1 收縮算子Y的更新

將變量E,X,Z固定，更新Y的最優(yōu)化模型(6-1)可等價為

(7)

為了求解上述核范數(shù)最小化問題，給出以下引理：

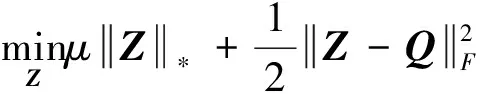
本研究仍然使用奇異值分解的方法求解問題(7)，與未使用矩陣三分解的模型需要對m×n維的矩陣進行奇異值分解不同，只需要對r×r維的矩陣進行奇異值分解，其中r?min(m,n)。

因此，TFM方法可以大大降低計算的復(fù)雜度。由引理知，模型(7)的最優(yōu)解為

(8)

2.2 利用軟閾值算子更新E

為了求解變量E，固定變量Y,X,Z，可將模型(6-2)轉(zhuǎn)化為如下優(yōu)化模型

為了得到Ek+1的最優(yōu)解，需先確定EΩ和EΩC分別對應(yīng)的兩個子問題。其中，EΩ對應(yīng)的子問題為

(9)

對問題(9)利用軟閾值算子進行求解，可得其最優(yōu)解為

(10)

另外，EΩC對應(yīng)的子問題為

(11)

由問題(11)的最優(yōu)性條件可得其最優(yōu)解為

(12)

2.3 利用Orthogonal Procrustes更新X和Z

為了求解變量X和Z，分別將模型(6-3)和(6-4)轉(zhuǎn)化為以下兩個子問題

(13)

(14)

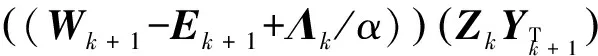
可得X和Z的最優(yōu)解分別為

(15)

(16)

求解模型(5)的算法如下：

算法：求解模型(5)的增廣拉格朗日方法輸入：數(shù)據(jù)矩陣W∈Rm×n，λ>0；初始化：令E=E0，X=X0，Y=Y0，Z=Z0，Λ=Λ0；步驟1：根據(jù)(8)式計算Yk+1；步驟2：根據(jù)(10)式和(12)式計算Ek+1；步驟3：根據(jù)(15)式計算Xk+1；步驟4：根據(jù)(16)式計算Zk+1；步驟5：根據(jù)(6?5)式更新拉格朗日乘子Λk+1；直到收斂；輸出：Y?=Yk+1，E?=Ek+1，X?=Xk+1，Z?=Zk+1

3 數(shù)值實驗

將提出的基于矩陣三分解方法的RMC模型應(yīng)用于人臉識別的實際問題中，利用Yale-B人臉數(shù)據(jù)集中的Man face數(shù)據(jù)集和Woman face數(shù)據(jù)集，與原始RMC模型和使用RBF方法的RMC模型進行迭代次數(shù)、運行時間的比較。實驗運行環(huán)境為Pentium E5500 2.77 GHz雙核處理器，內(nèi)存2.00 GB。所有算法程序均由Matlab R2014a編寫。

3.1 參數(shù)設(shè)置

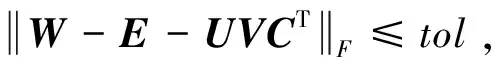
3.2 實驗結(jié)果

將本研究提出的TFMC模型與RMC模型和使用RBF方法的RMC模型進行對比實驗，迭代次數(shù)與運行時間的比較結(jié)果見表1。可見，在不同數(shù)據(jù)集中，本研究所用算法較RMC和RBF方法的迭代次數(shù)和運行時間均有很大程度的降低。

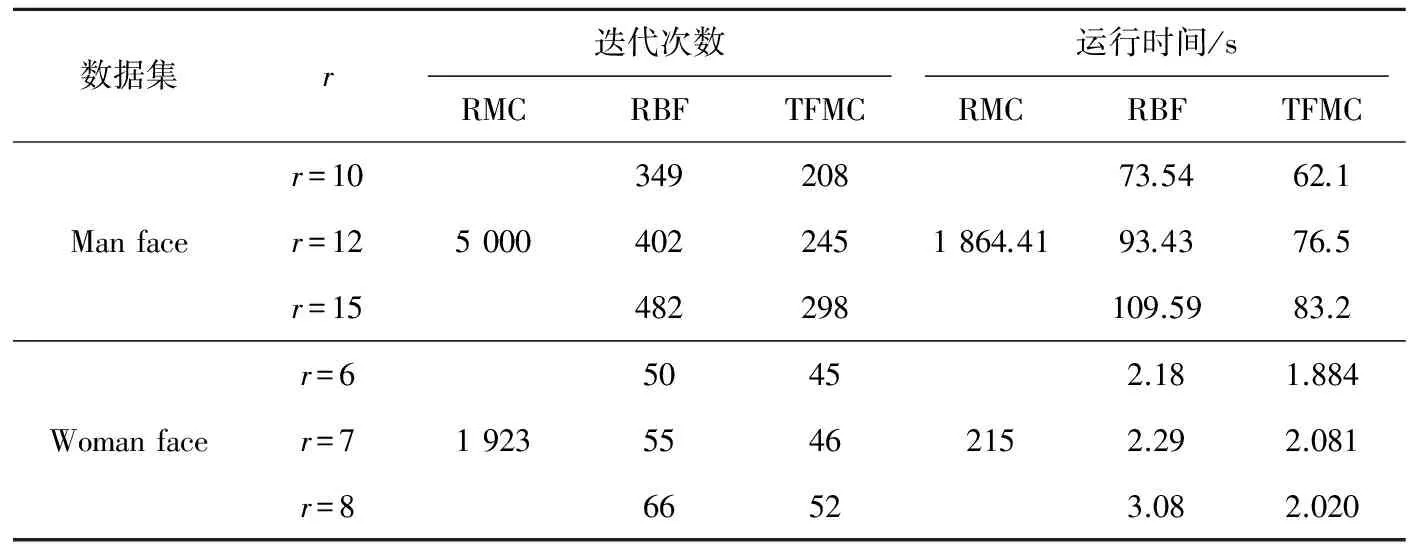
表1 迭代次數(shù)與運行時間的比較結(jié)果Tab.1 Comparison results of iteration times and running time

考慮到矩陣補全的目的是恢復(fù)含有損失函數(shù)的數(shù)據(jù)矩陣，因此為了進一步顯示本文方法的有效性，Man face數(shù)據(jù)集取秩分別為10、12、15，Woman face數(shù)據(jù)集取秩分別為6、7、8進行數(shù)值實驗。由圖1、圖2可以看出，本研究方法均可以比較完美的恢復(fù)原有的模樣。另一方面，雖然已知數(shù)據(jù)的尺寸非常大，但由于本研究采用的矩陣三分解方法對問題進行了大幅度的降階，使得當(dāng)r較小時，算法的運算時間大大減少。Man face數(shù)據(jù)集中，當(dāng)r=10,12,15時，算法的運算時間分別為62.1、76.5和83.2 s. Woman face數(shù)據(jù)集中，當(dāng)r=6,7,8時，算法的運算時間分別為1.884、2.081和2.020 s。

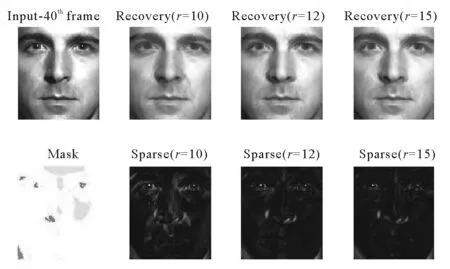
其中Input-40表示輸入的第40張原始圖片；Mask中紅色表示閉塞像素，黃色表示飽和像素；第一行的后三列表示秩為10、12、15的恢復(fù)圖片；第二行后三列表示秩為10、12、15的噪聲圖片。圖1 Manface數(shù)據(jù)集秩分別為10、12、15時對應(yīng)的恢復(fù)效果圖Fig.1 The recovered images from Man face data set’s rank-10, rank-12 and rank-15 factorization

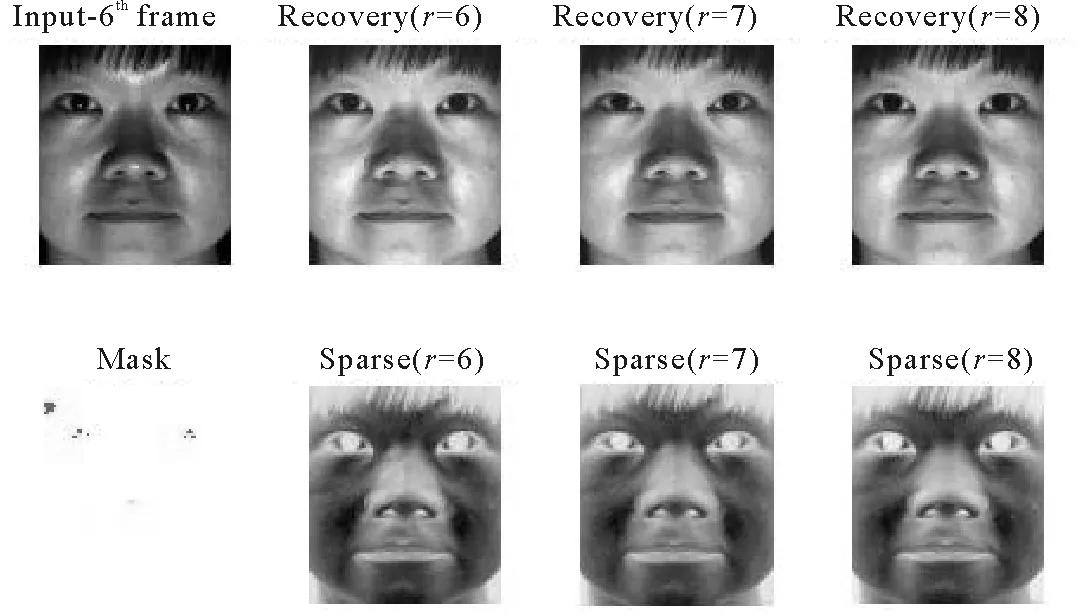
其中Input-6表示輸入的第6張原始圖片；Mask中紅色表示閉塞像素，黃色表示飽和像素；第一行的后三列表示秩為6、7、8的恢復(fù)圖片；第二行后三列表示秩為6、7、8的噪聲圖片。圖2 Woman face數(shù)據(jù)集秩分別為6、7、8時對應(yīng)的恢復(fù)效果圖Fig.2 The recovered images from Woman face data set’s rank-6, rank-7 and rank-8 factorization

4 總結(jié)

針對人臉識別中的矩陣補全模型，求解過程中存在計算復(fù)雜度過大的問題提出使用三分解方法降低計算的復(fù)雜度，并應(yīng)用交替方向乘子法進行求解。數(shù)值實驗結(jié)果表明，設(shè)計的模型迭代次數(shù)少，計算時間短。隨著數(shù)據(jù)集中數(shù)據(jù)量的不斷增大，本模型和算法將有更廣闊的應(yīng)用前景。

參考文獻：

[1]彭義剛，索津莉，戴瓊海，等.從壓縮傳感到低秩矩陣恢復(fù):理論與應(yīng)用[J].自動化學(xué)報，2013，39(7):981-994.

PENG Yigang,SUO Jinli，DAI Qionghai，et al.From compressed sensing to low-rank Matrix recovery:Theory and applications[J].Acta Automatica Sinica，2013，39(7):981-994.

[2]馬堅偉, 徐杰, 鮑躍全,等. 壓縮感知及其應(yīng)用:從稀疏約束到低秩約束優(yōu)化[J]. 信號處理, 2012, 28(5):609-623.

MA Jianwei，XU Jie，BAO yuequan，et al.Compressive sensing and its application: From sparse to low-rank regularized optimization[J]. Signal Processing，2012, 28(5):609-623.

[4]張婷婷.基于低秩矩陣填充與恢復(fù)的圖像去噪方法研究[D].天津：河北工業(yè)大學(xué)，2015.

[6]SHI J，ZHENG X，YONG L.Incomplete robust principal component analysis[J].ICIC Express Letters.Part B，Applications:An International Journal of Research and Surveys，2014，5(6):1531-1538.

[7]SHANG F，LIU Y，TONG H，et al.Robust bilinear factorization with missing and grossly corrupted observations[J].Information Sciences，2015，307:53-72.

[8]XU Y，YIN W，WEN Z，et al.An alternating direction algorithm for matrix completion with nonnegative factors[J].Frontiers of Mathematics in China，2012，7(2):365-384.

[9]ZHENG Y，LIU G，SUGIMOTO S，et al.Practical low-rank matrix approximation under robust l1-norm[C]∥IEEE Conference on Computer Vision and Pattern Recognition (CVPR)，2012:1410-1417.

[10]DING C，LI T，PENG W，et al.Orthogonal nonnegative matrix t-factorizations for clustering[C]∥Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM，2006:126-135.

[11] LIU Y, JIAO L C, SHANG F. An efficient matrix factorization based low-rank representation for subspace clustering[J]. Pattern Recognition, 2013, 46(1):284-292.

[12]CAI J F，CANDS E J，SHEN Z.A singular value thresholding algorithm for matrix completion[J].SIAM Journal on Optimization，2010,20(4):1956-1982.