多維視角，殊途同歸
——2017年山東卷文科第12題“十法”

☉江蘇省泗洪中學 楊東進

在高中數學中，求函數的最值、值域問題，二元代數式的最值問題，是各類考試中比較常見的題型，也是高考中常見的考點之一.此類問題比較常見的方法有基本不等式法、待定系數法、導數法、換元法（三角換元等）、柯西不等式等.下面結合2017年高考山東卷文科第12題二元代數式的最值問題來加以實例剖析，結合多維視角切入，達到殊途同歸.

高考真題 （2017年山東卷文12）若直線（a＞0，b＞0）過點（1，2），則2a+b的最小值為______.

思路分析1：根據直線過定點得到關系式結合代數式2a+b乘“1”展開，結合基本不等式來確定最小值即可.

解法1：基本不等式法1.

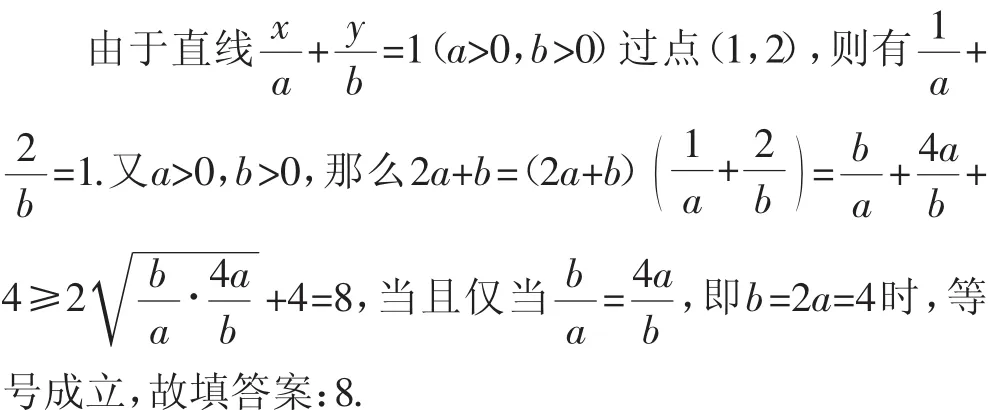
解法2：基本不等式法2.

解法3：基本不等式法3.

思路分析4：根據直線過定點得到關系式直接利用基本不等式得到ab≥8，再結合代數式2a+b，再次利用基本不等式來確定最小值問題，兩次利用基本不等式要注意等號成立的條件的一致性.

解法4：基本不等式法4.

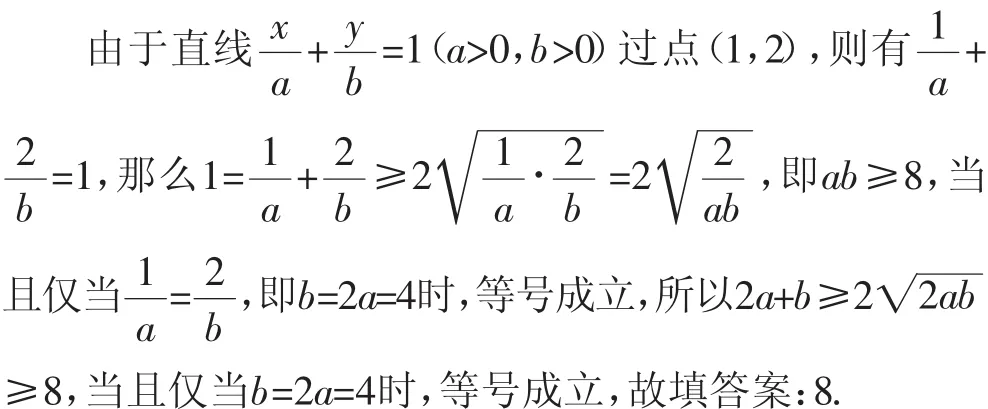
思路分析5：根據直線過定點得到關系式直接利用基本不等式得到ab≥8，并結合此時等號成立的條件，代入關系式+=1得到2a+b=ab，進而確定代數式2a+b的最小值問題.

解法5：基本不等式法5.

由于直線+=1（a＞0，b＞0）過點（1，2），則有+且僅當=，即b=2a=4時，等號成立，由+=1可得2a+b=ab≥8，故填答案：8.

思路分析6：根據直線過定點得到關系式+=1，根據關系式的轉化用含參數a的關系式來表示b，代入代數式2a+b得到含有a的關系，設其最小值為M，通過求解二次方程，根據判別式來確定關系式的最小值即可.

解法6：待定系數法.

由于直線.又b＞0，所以a＞1，那么設≥M（M為正實數），整理可得2a2-Ma+M≥0，則Δ=M2-8M≥0，解得M≥8或M≤0（舍去），則2a+b的最小值為8，故填答案：8.

解法7：導數法1.

思路分析8：根據直線過定點得到關系式根據關系式的轉化用含參數a的關系式來表示b，代入代數式2a+b得到f（a），通過求導，結合函數的單調性與極值來確定函數關系式的最小值即可.

解法8：導數法2.

由于直線+=1（a＞0，b＞0）過點（1，2），則有+=1，可得=1-，即b=.又b＞0，所以a＞1，那么，令f′（a）=0，解得a=2（由于a＞1）.當a∈（0，2）時，f′（a）＜0，f（a）單調遞減；當a∈（2，+∞）時，f′（a）＞0，f（a）單調遞增.所以f（a）min=f（2）=8，即當a=2，b=4時，2a+b的最小值為8，故填答案：8.

思路分析9：根據直線過定點得到關系式進而通過三角換元，結合代數式2a+b的轉化，通過三角恒等變換公式，并結合三角函數的圖像與性質來確定最小值即可.

解法9：三角函數法.

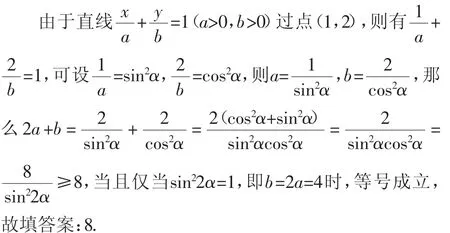
思路分析10：根據直線過定點得到關系式結合代數式2a+b乘“1”，利用柯西不等式來確定最小值即可.

解法10：柯西不等式法.

解決此類和式定值求最值問題的比較常用的方法是利用基本不等式來確定最值，利用基本不等式時的切入點不同導致方法各異；而利用待定系數法，通過轉化，結合判別式，通過解不等式來確定參數的最值問題；而利用已知關系式的轉化，轉化為含有一個參數的代數式，通過函數求導，結合函數的單調性、極值與最值來確定最值問題；而根據和式定值為1的性質可以利用三角換元來處理，結合三角恒等變換，通過三角函數的圖像與性質來確定最值；而利用柯西不等式來確定最值也別有特色，特別對于三元及三元以上的問題顯得更加有效果.F