基于MPC的重型液罐車側(cè)向穩(wěn)定性控制仿真

于志新, 程新新, 李 杰, 李紹松

(1.長春工業(yè)大學(xué) 機(jī)電工程學(xué)院， 吉林 長春 130012;2長春工業(yè)大學(xué) 汽車工程研究院， 吉林 長春 130012)

0 引 言

我國公路運輸線四通八達(dá)，各種油品、危化品主要依靠半掛液罐車運輸，液罐車具有裝載量大、運輸成本低的特點，逐漸成為公路運輸?shù)闹黧w。因其具有載量大、重心高、輪距相對較小等特點，并且在轉(zhuǎn)向或變道過程中罐內(nèi)液體易受激勵產(chǎn)生晃動，與車體的耦合運動會導(dǎo)致車輛發(fā)生側(cè)傾失穩(wěn)，這在道路運輸是極其危險的狀況。國內(nèi)外學(xué)者針對罐車側(cè)傾問題在罐內(nèi)液體晃動分析和罐內(nèi)結(jié)構(gòu)優(yōu)化上做了大量研究[1-6]，但液體的晃動對整車的側(cè)向穩(wěn)定性分析相對較少。因此，通過對罐車實施主動安全控制，提高液罐車的穩(wěn)定性是一種更適用和高效的方法[7-11]。

1 液體晃動分析

以某專用汽車制造廠生產(chǎn)的44 m3半掛液罐車為分析對象，考慮到罐體長度相對較長,忽略罐車兩端封頭以及內(nèi)部附加結(jié)構(gòu)影響，并且罐車在平直路面上轉(zhuǎn)彎或避障時，罐體內(nèi)的軸向運動視為不變，因此選取單位長度上罐體進(jìn)行建模分析，并作如下假設(shè)：

1)液體為理想不可壓縮的；

2)不考慮罐內(nèi)氣體的影響；

3)不考慮罐體的變形。

罐內(nèi)液體坐標(biāo)系如圖1所示。

圖1 罐內(nèi)液體坐標(biāo)系

圖中：x----車輛行駛方向;

y----駕駛員左側(cè);

z----豎直向上;

Ω----流體域;

Σ----罐體濕表面;

S----自由面液度;

h0----液面到x軸距離;

θ0----自由液面和罐體交點與坐標(biāo)原點連線同z負(fù)半軸的夾角。

液體在罐內(nèi)的運動方程滿足以下三個條件：

1)在Ω內(nèi)連續(xù)；

2)在Σ內(nèi)不可滲透；

3)在S上滿足運動學(xué)和動力學(xué)條件。

得到以下方程：

(1)

流體勢函數(shù)分解為液體隨罐體運動而產(chǎn)生的剛性分量φu(r,θ,t)以及液體晃動產(chǎn)生的動壓力分量φs(r,θ,t)兩個子函數(shù)和的形式[12]：

φ=φs(r,θ,t)+φu(r,θ,t)

(2)

其中,φu(r,θ,t)和φs(r,θ,t)都滿足式(1)，可以得到

液體自由晃動時，令

φ=iσΦ(r,θ)eiσt

η=H(r,θ)eiσt

則式(1)可化為：

(3)

式中:Φ----晃動模態(tài)函數(shù);

H----波高模態(tài)函數(shù)；

ω----液體自由晃動特征頻率。

運用Galerkin法求出上式中的ω和Φ。

當(dāng)罐體中的液體被動晃動時，自由晃動模型同樣適用于受迫晃動。

令φ、η為自由晃動特征模態(tài)Φ、H的線性組合，即：

(4)

式中:qi(t)----廣義坐標(biāo)。

將式(4)代入式(1)中，并消去η得

(5)

對上式同乘ρHi，然后在S上作積分，便可得到以下的積分形式：

(6)

其中

液體晃動時，前面已假設(shè)液體為理想的不可壓縮的流體，忽略了液體之間的相互作用力。但實際上液體之間還有一定的阻尼作用，且無法忽略，于是為簡化計算，可在方程中加入比例阻尼項，即：

C=?0M+?1K

(7)

其中,?0，?1為常數(shù)。式(6)變?yōu)?/p>

(8)

滿足精度要求的條件下，截取式(8)一定階數(shù)的近似計算。求解qi(t),即可得到

(9)

2 液體側(cè)向晃動力影響分析

2.1 側(cè)向晃動受力分析

液體之間存在流體力和流體勢，根據(jù)兩者之間函數(shù)關(guān)系可解出與液體對罐車內(nèi)壁上的力。流體壓強(qiáng)為:

式中：z′----自由液面到所求點的垂直距離。

對單位長度上的靜、動壓力在罐體長度上積分得到罐體的慣性力Fu、動壓力Fs:

(10)

則作用在罐體上的側(cè)向合力為：

(11)

其中

Gi=ρ21-iR1-iZiL

2.2 充液比對液體晃動的影響

液罐車罐內(nèi)液體與罐體參數(shù)如下：

1)液體密度:ρ=580 kg/m3;

2)罐體半徑：R=1.5 m;

3)罐體長度:L=12 m。

充液比λ為液體高度與罐體半徑的比，截取式(8)的前四階，計算出在不同充液比下罐體受液體慣性作用力Fu、液體晃動作用力Fs以及兩者的合力Fh。側(cè)向受力隨充液比的變化如圖2所示。

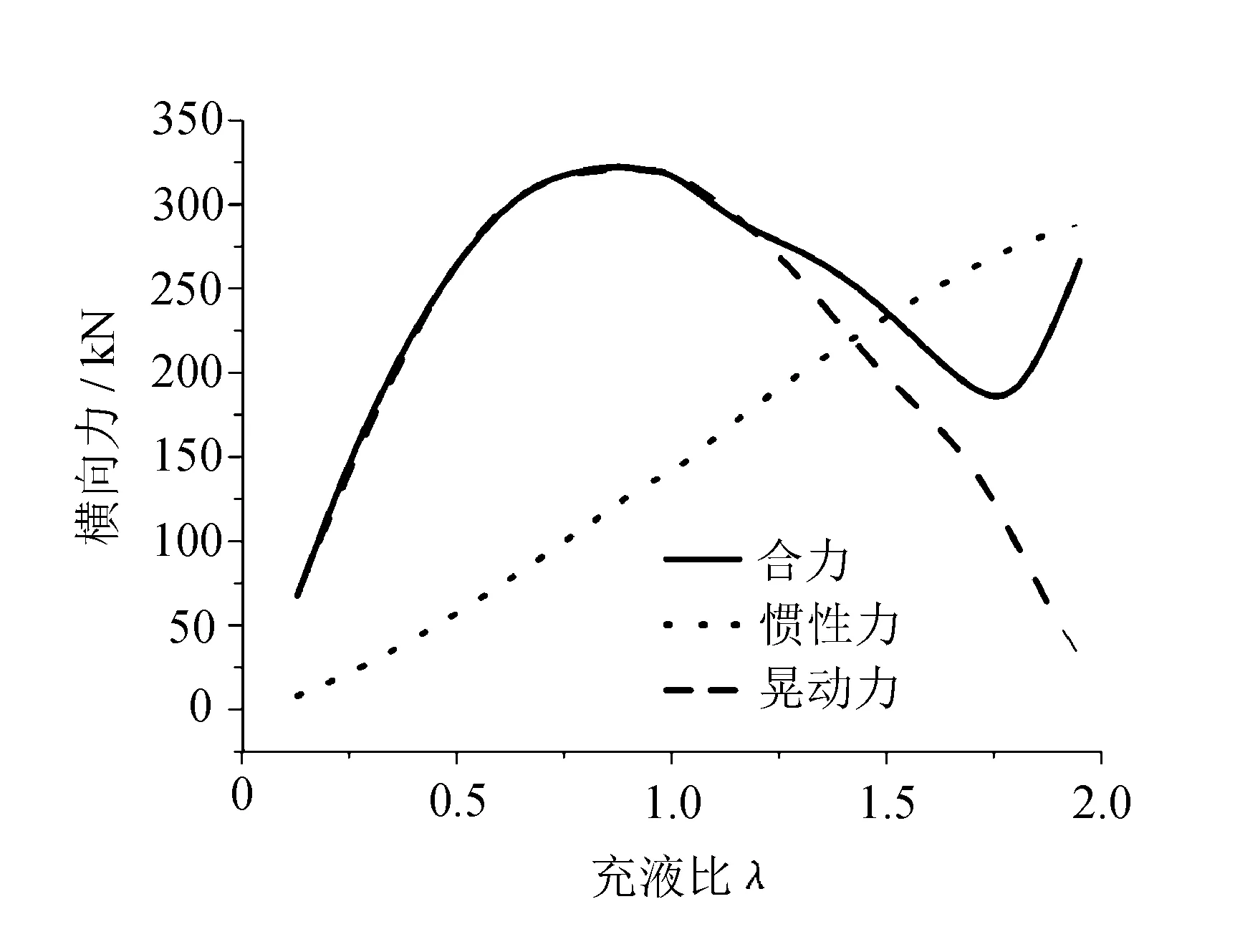
圖2 側(cè)向受力隨充液比的變化圖

由圖2可知，在λ∈[0,1]內(nèi)，充液比與慣性力之間呈線性關(guān)系，逐漸升高。慣性力在λ=1時達(dá)到最大值；在圖中晃動力如同慣性力一樣呈現(xiàn)出先增大后減小的趨勢；而二者的合力在充液比小時與晃動力表現(xiàn)出相同的變化趨勢，并在充液比λ=1.5時，因慣性力作用越來越明顯，合力反而表現(xiàn)出不減反增的趨勢，但未超過晃動最為劇烈時的最大值。

2.3 側(cè)向加速度對液體晃動的影響

液罐車側(cè)向受力不僅受充液比的影響，而且還受側(cè)向加速度的影響。在此選取充液比λ=1，以埃爾森特羅EI地震波為激勵，計算液罐車受到的慣性力矩、晃動力矩和合力矩。側(cè)向加速度激勵如圖3所示。

圖3 側(cè)向加速度激勵圖

液罐車所受到的慣性力矩、晃動力矩和合力矩如圖4所示。

從圖4中可知,在λ=1條件下，慣性力矩與晃動力矩的幅值相同時，罐體受到劇烈的晃動，此時罐體極易表現(xiàn)出側(cè)向不穩(wěn)定，有側(cè)翻的危險。

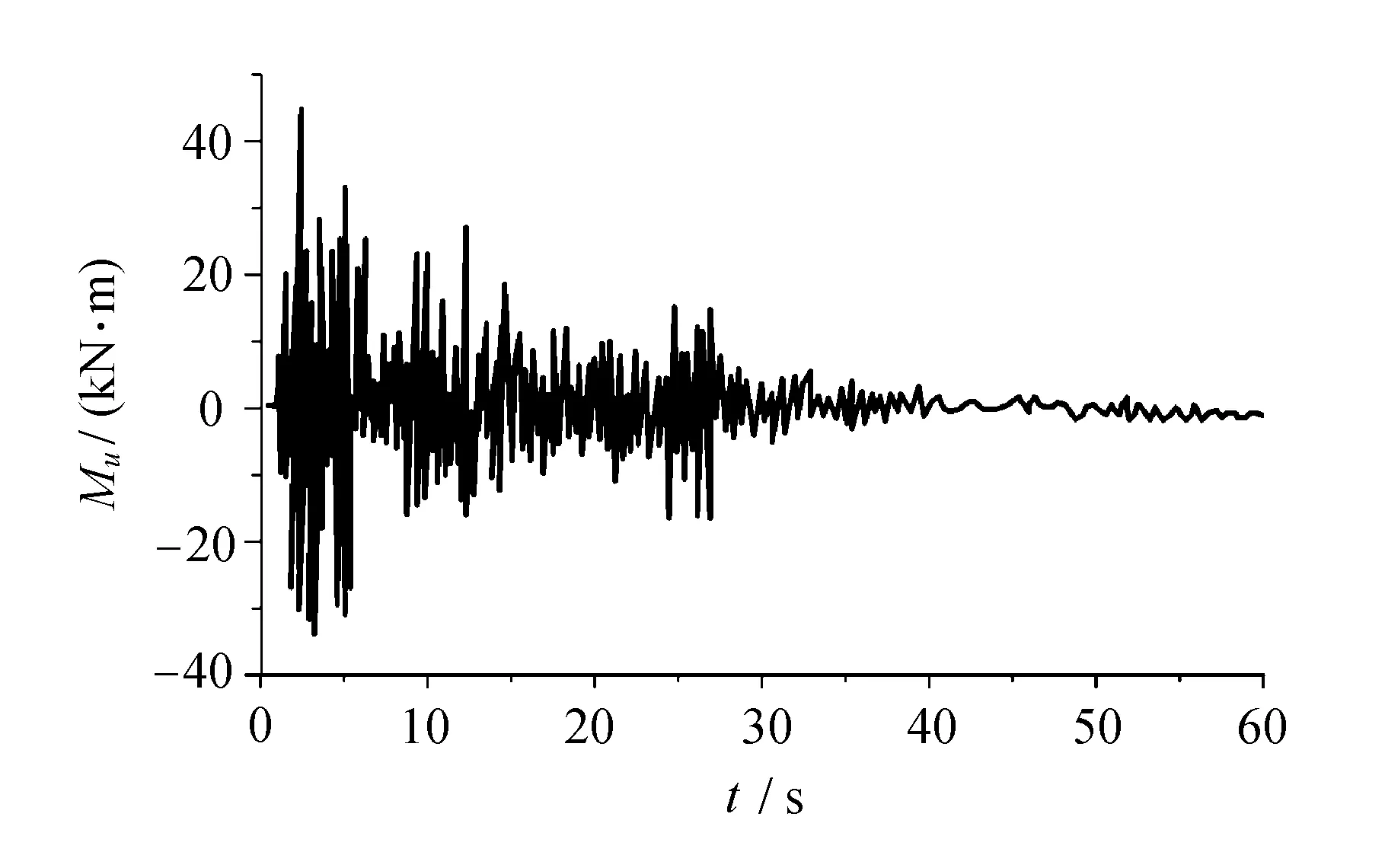
(a) 慣性力矩

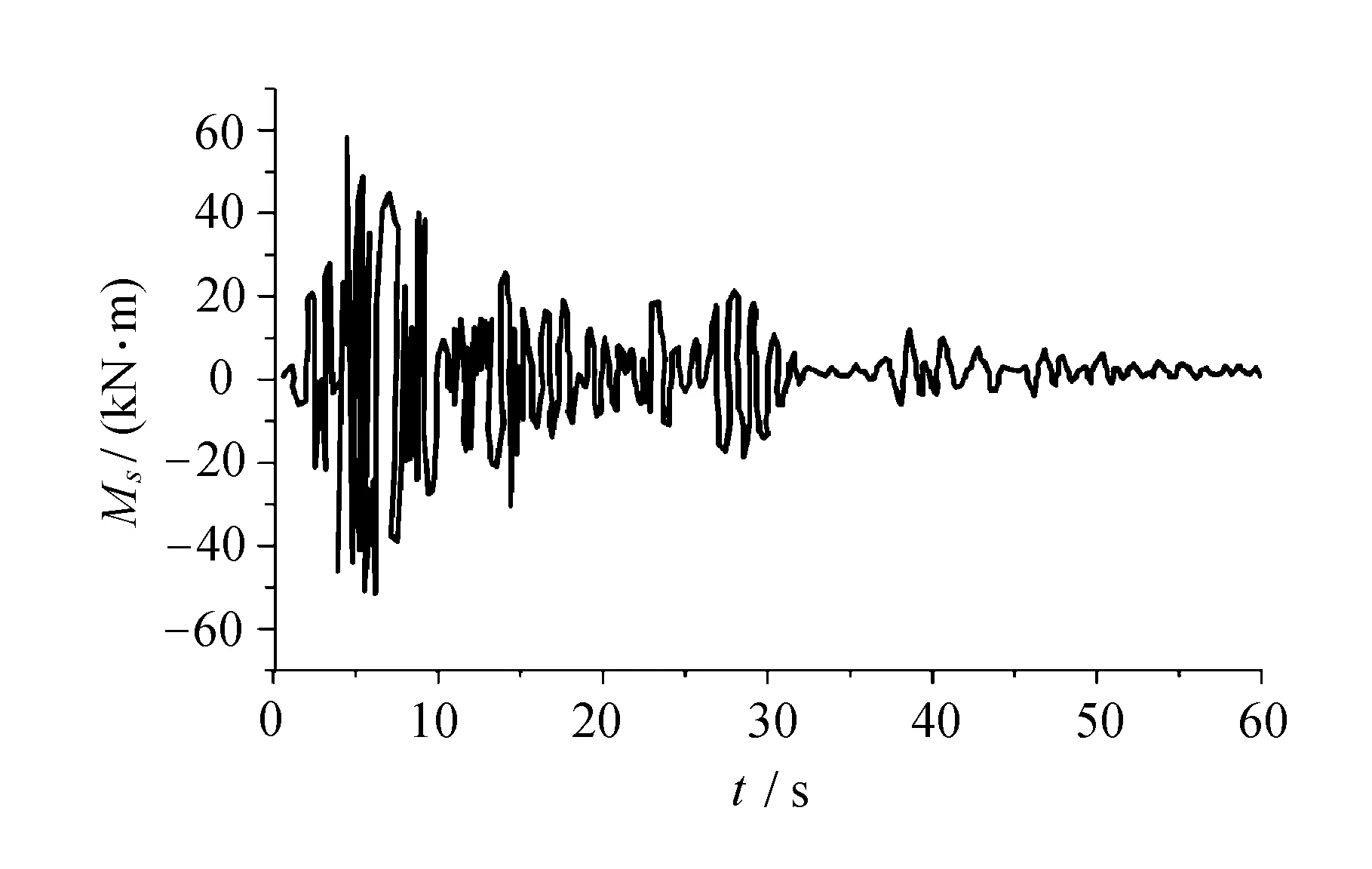
(b) 晃動力矩

(c) 合力矩

但由于慣性力矩和晃動力矩的相位不同，即兩者之間的相互作用并不是代數(shù)相加，它在實際運動中與很多因素相關(guān)。因此,在實際的運動過程中應(yīng)盡量避免在此類工況下行駛。

3 液體晃動對車輛運動狀態(tài)的影響

由于液罐車質(zhì)量和體積較大，若進(jìn)行實車實驗危險過大。在此應(yīng)用仿真方法分析液體晃動對液罐車穩(wěn)定性的影響。對比相同的工況下，罐內(nèi)等質(zhì)量的固體與液體的運動分別對液罐車穩(wěn)定性的影響。液體晃動對罐車穩(wěn)定性影響流程如圖5所示。

圖5 液體晃動對罐車穩(wěn)定性影響流程圖

仿真液罐車的幾個重要參數(shù)：

1)充液比λ=1；

2)車速v=40 km/h；

3)角階躍輸入方向盤轉(zhuǎn)角如圖6所示。

圖6 角階躍輸入方向盤轉(zhuǎn)角

分別對一定質(zhì)量的液體和等效質(zhì)量的固體進(jìn)行仿真，可得到穩(wěn)定性仿真曲線如圖7所示。

圖7表明，在角階躍輸入下，與等效質(zhì)量的固體相比，液體對液罐車穩(wěn)定性的影響最大。這是因為液體的晃動增加了整體受力的不均勻，使得整車動力穩(wěn)定性變差。

(a) 側(cè)傾角

(b) 橫擺角速度

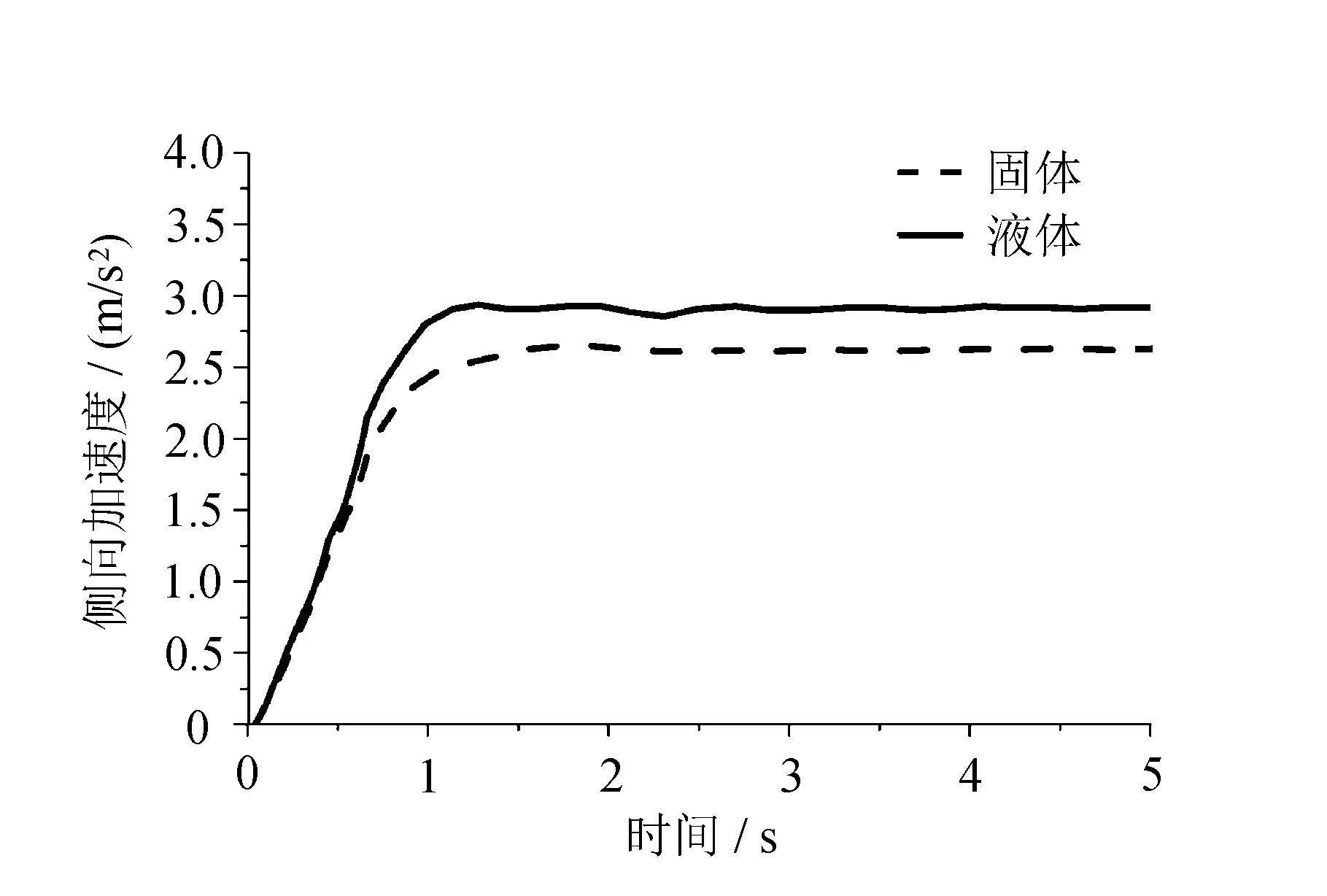
(c) 側(cè)向加速度

4 半掛液罐車動力學(xué)模型

考慮整車的側(cè)向、橫擺運動及側(cè)傾運動,采用三自由度車輛簡化模型，如圖8所示。

(a) 橫擺

牽引車運動方程

(12)

(13)

(14)

半掛車運動方程

(15)

(16)

(17)

兩剛體運動約束方程

(18)

文中采用線性輪胎模型，則有：

(19)

式中：m1,m2----分別為牽引車、半掛車質(zhì)量;

β1,β2----分別為牽引車、半掛車的質(zhì)心側(cè)偏角;

ψ1,ψ2----分別為牽引車、半掛車的質(zhì)心橫擺角;

m1s,m2s----分別為牽引車和半掛車的簧載質(zhì)量;

Fi----第i輪的側(cè)向力;

F4----半掛車對牽引車的作用力;

Φ1,Φ2----分別為牽引車、半掛車簧載質(zhì)量側(cè)傾角;

I1xx,I2xx----分別為牽引車、半掛車簧載質(zhì)量側(cè)傾轉(zhuǎn)動慣量;

I1zz,I2zz----分別為牽引車、半掛車橫擺轉(zhuǎn)動慣量;

u1,u2----分別為牽引車、半掛車行駛車速;

kr1,kr2----分別為牽引車、半掛車側(cè)傾剛度;

c1,c2----分別為牽引車、半掛車側(cè)傾角阻尼;

k12----第五輪側(cè)傾剛度;

h1c,h2c----分別為牽引車、半掛車質(zhì)心高度;

h1,h2----分別為牽引車、半掛車質(zhì)心到各自側(cè)傾軸線的距離;

Γ----鉸接角;

a,b,c----分別為牽引車重心到前軸、后軸、鉸接點的距離;

d,e----分別為半掛車重心到后軸、前軸的距離。

5 集成模型預(yù)測控制器設(shè)計

實際的期望質(zhì)心側(cè)偏角和橫擺角速度可以作為模型預(yù)測控制器的輸入，該控制器的輸出為附加的橫擺力矩和前輪轉(zhuǎn)角。

為了獲得側(cè)向穩(wěn)定性，實際的橫擺角速度應(yīng)接近期望的橫擺角速度。文中設(shè)計了三自由度整車模型。整車模型狀態(tài)空間方程如下:

(20)

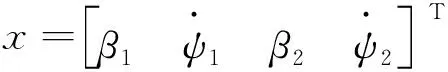
則有：

實際中為保證側(cè)向和側(cè)傾的穩(wěn)定性，橫擺角速度和質(zhì)心側(cè)偏角都應(yīng)當(dāng)被限制在穩(wěn)定閾值內(nèi)。期望的橫擺角速度可通過穩(wěn)定參考模型得到：

(21)

式中：

此外，期望的橫擺角速度應(yīng)受到路面附著系數(shù)的約束：

(22)

穩(wěn)態(tài)轉(zhuǎn)向時，文中假設(shè)牽引車與掛車期望的橫擺角速度相同，即

ψ1ref=ψ2ref

為了阻止轉(zhuǎn)向過程中整車的側(cè)傾，期望的質(zhì)心側(cè)偏角可選為零，即

β1ref=β2ref=0

整車狀態(tài)空間模型離散化得到如下簡約模型：

x(k+1)=F(x(k),u(k))

y(k)=Gx(k)

(23)

在k時刻的車輛狀態(tài)，依據(jù)上述公式可以預(yù)測接下來Np步的動力學(xué)狀態(tài)，表述如下：

x(k+Np)=F(x(k),u(k),u(k+1),…,

u(k+Nu),…,u(k+Np-1))

式中:Nu----控制時域;

Np----預(yù)測時域。

由文獻(xiàn)[13]可知，前輪主動轉(zhuǎn)向電機(jī)的控制周期為10～30 ms，沒有ABS的液壓制動系統(tǒng)的移動周期為20～50 ms，考慮到采樣周期應(yīng)同時滿足上述兩個條件，即文中采用的采樣時間Ts=20 ms，當(dāng)采樣時間超過控制時域，假設(shè)控制輸入到預(yù)測時域之間保持不變，即為：

u(k+Nu-1)=u(k+Nu)=

u(k+Nu+1)=

…=

u(k+Np-1)

在k時刻的最優(yōu)控制序列U(k)和響應(yīng)的預(yù)測輸出為：

其中,y(k+i|k),i=1,2,…,Np，可由式(23)得出。

考慮到控制的要求為實際橫擺角速度與期望橫擺角速度相匹配。期望橫擺角速度公式如下：

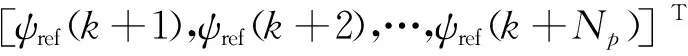
控制罐車穩(wěn)定性所需要的額外橫擺力矩是由執(zhí)行器(制動器的差動制動)而來，為了防止罐車側(cè)翻，該額外橫擺力矩應(yīng)有如下約束：

(24)

此外由于汽車結(jié)構(gòu)的限制，罐車的前輪轉(zhuǎn)向角度也有一定的約束范圍：

δmin≤δ(k)≤δmax

(25)

當(dāng)罐車進(jìn)入彎道或變道時，其實際橫擺角速度應(yīng)很快與期望的橫擺角速度匹配，于是使目標(biāo)函數(shù)J1=‖(Y(k+1|k)-R(k+1))‖2值最小。此外,為了使輸入平穩(wěn)順滑，目標(biāo)函數(shù)J2=‖U(k)‖2值也應(yīng)最小。于是聯(lián)立J1，J2就可得到整車控制的目標(biāo)函數(shù)：

J(Y(k),U(k),Nu,Np)=‖Qy(Y(k+1|k)-R(k+1))‖2+‖QuU(k)‖2

(26)

式中：Qy,Qu----權(quán)重矩陣。

為了得到上述目標(biāo)函數(shù)的最優(yōu)解，就要基于約束條件式(24)、式(25)求解。

當(dāng)?shù)玫阶顑?yōu)控制序列U(k)，選取k時刻最優(yōu)控制序列中的第一個值作為k+1時刻的輸入。然后整個預(yù)測時域向前移動一個間隔，在重復(fù)滾動優(yōu)化得到此后的最優(yōu)控制值。模型控制框圖如圖9所示。

圖9 液罐車穩(wěn)定性控制框圖

6 仿真結(jié)果分析

為了驗證控制策略的有效性，選擇極限條件下的魚鉤工況進(jìn)行仿真，在該工況下，液罐車的失穩(wěn)基本表現(xiàn)為側(cè)翻事故。針對液體晃動降低液罐車行駛穩(wěn)定性，以三自由度半掛液罐車為參考模型，采用模型預(yù)測控制計算出最優(yōu)的附加橫擺力矩，制定差動制動的控制方案來分配附加橫擺力矩，經(jīng)仿真分析對比得出液罐車側(cè)傾角、橫擺角速度、側(cè)向加速度曲線如圖10所示。

(a) 方向盤角輸入

(b) 側(cè)傾角

(c) 橫擺角速度

(d) 側(cè)向加速度

由圖(10)可以看出，未施加控制的半掛液罐車側(cè)傾角會出現(xiàn)急劇的變化，側(cè)向加速度超過重型車輛的側(cè)翻閾值0.4 g，施加控制的液罐車側(cè)向加速度穩(wěn)定在0.3 g內(nèi)，未施加控制的液罐車比有控制的側(cè)向加速和橫擺角速度跳動的幅度范圍更大。在7.5 s時未施加控制的液罐車側(cè)傾角發(fā)散，此時車輛已經(jīng)發(fā)生側(cè)翻，而施加控制后液罐車側(cè)傾角收斂，始終在穩(wěn)定閾值內(nèi)。

7 結(jié) 語

1)根據(jù)勢流理論建立了液罐車罐體內(nèi)液體的運動方程，分析了液體晃動特性和影響因素。在λ=1時，液體晃動最劇烈。

2)為研究液體晃動對液罐車穩(wěn)定性的影響，在角階躍輸入下進(jìn)行裝載固液貨物對比仿真試驗，試驗表明，與裝載固體貨物相比，液罐車的側(cè)傾角和橫擺角出現(xiàn)較大的變化，液體的晃動對整車穩(wěn)定性影響較大。

3)在極限工況下仿真分析結(jié)果表明，設(shè)計的模型預(yù)測控制策略能夠有效地提高車輛行駛穩(wěn)定性。

參考文獻(xiàn)：

[1] Welt F, Modi V J. Vibration damping through liquid sloshing, Part Ⅰ: A nonlinear analysis[J]. ASME Transactions, Journal of Vibration and Acoustics,1992,114(1):10-16.

[2] Chen C, Tomizuka M. Lateral control of commercial heavy vehicle[J]. International Journal of Vehicle Mechanics and Mobility,2000,33(6):391-420.

[3] Yan G R, Subhash Rakheja, Siddiqui K. Analysis of transient fluid slosh in partly-filled tanks with and without baffles: Part 1:Model validation[J]. International Journal of Heavy Vehicle Systems. 2010，17(3):359 -379.

[4] Iman Hazrati Ashtiani, Mehrnoosh Abedi. Effects of Liquid Cargo on Lateral Stability of B-Train Combination[C]//SAE Technical Paper,2014-01-2319.

[5] 岳寶增,祝樂梅,于丹.儲液罐動力學(xué)與控制研究進(jìn)展[J].力學(xué)進(jìn)展,2011,41(1):79-91.

[6] 趙樹恩，趙靈鶴.汽車罐車橫向運動液體晃動動力學(xué)特性模擬[J].應(yīng)用數(shù)學(xué)和力學(xué),2014,35(11)：1259-1270.

[7] Avesta Goodarzi. Integrated Yaw and Roll Moments Control of Articulated Vehicles[C]//SAE Paper，2009-01-2874.

[8] Ji Y, Guo H Y, Chen H, et al. Integrated control of active front steering and direct yaw moment based on model predictive control[C]//6th chin. Control Decis. Conf. Changsha, China,2014,34(2):2044-2049.

[9] Jianbo Lu, David Messih. An enhancement to an electronic stability control system to include a rollovercontrol function[C]//SAE Paper,2007-01-0809.

[10] 于志新，宗長富.基于LQR的重型半掛汽車列車穩(wěn)定性控制策略[J].中國公路學(xué)報,2011,24(2)：114-119.

[11] 趙偉強(qiáng)，封冉，宗長富.基于等效晃動模型的液罐車防側(cè)翻控制策略[J].吉林大學(xué)學(xué)報：工學(xué)版，2018，48(1):30-35.

[12] 盧軍.任意充液比油罐車液體晃動及整車橫向穩(wěn)定性研究[D].成都:西南交通大學(xué),2009.

[13] Bing Zhu, Qi Piao, Jian Zhao, et al. Integrated chassis control for vehicle rollover prevention with neural network time-to-rollover warning metrics[J]. Advances in Mechanical Engineering，2016,8(2):1-13.