為數(shù)學點贊
——為名師例析數(shù)學文化（5）統(tǒng)計與統(tǒng)計案例

■北京市教育學院豐臺分院 張 琦

■北京市第十二中學高中部 高慧明

本刊特邀欄 介:

高慧明首 佳班主任,全國著名數(shù)學特級教師,國家教育部課程改革“全國先進工作者”,全國著名高考數(shù)學命題與考試研究專家,國家教育部“國培計劃”全國中小學教師培訓、班主任培訓、校長培訓特邀主講專家,受邀在全國各地做有關(guān)高考科學備考、班級管理等多場專題報告。現(xiàn)任教于北京市第十二中學高中部。

隨著時代的發(fā)展,對“管理”的要求也越來越高,除對客觀現(xiàn)象進行定性分析以外,還需要進行相應(yīng)的定量分析,這時候“統(tǒng)計”發(fā)揮著重要的作用。在對“統(tǒng)計”進行介紹之前,我們先來欣賞二戰(zhàn)時期的數(shù)據(jù)分析故事。

第一則見于Cudmund R.Iversen和MaryGergen所著的《統(tǒng)計學——基本概念和方法》,故事如下。

第二次世界大戰(zhàn)期間,盟軍很想知道德軍總共制造了多少輛坦克。德國人長于邏輯思維而乏于機變,在給坦克編號時非常刻板,他們把坦克從1開始編號。戰(zhàn)爭之中,盟軍繳獲了一些德軍坦克,并記錄下了它們的生產(chǎn)編號。這些編號對于了解德軍的坦克總量有用處嗎?在統(tǒng)計學家眼里,這些編號組成了一個樣本,可由此去估計總的坦克數(shù)量。

制造出來的坦克數(shù)肯定不小于記錄中的最大編號,為了推測它比繳獲坦克中的最大編號大多少,可以先計算已知編號的平均值,并把這個平均值視為全部編號的中點。因此,樣本均值乘以2就是坦克總數(shù)的一個估計,當然,這里必須存在一個假設(shè):繳獲的坦克代表了所有坦克的一個隨機樣本。使用這種方法估計,有可能出現(xiàn)一個荒謬的結(jié)果:作為全部坦克數(shù)量估計值的樣本均值的2倍居然小于樣本中的最大值。另一種估計方法是用觀測到的最大編號乘以(1+1/n),如果繳獲坦克數(shù)量為1 0,其中最大編號為5 0,那么坦克總數(shù)的一個估計是5 0×(1+1/1 0)=5 5。這種方法的各種變形的確用于二戰(zhàn)之中。從戰(zhàn)后發(fā)現(xiàn)的德軍記錄來看,盟軍的估計值非常接近于德軍生產(chǎn)坦克的實際值。記錄還表明統(tǒng)計估計比其他情報方式所做的估計要大大接近于真實數(shù)目。統(tǒng)計學家做得比間諜們更漂亮!

第二則見于MichaelMorit在其Linkedin上發(fā)表的一篇有關(guān)數(shù)據(jù)挖掘在二戰(zhàn)里運用的文章之中。

二戰(zhàn)時狼群戰(zhàn)術(shù)的發(fā)明者鄧尼茨在一戰(zhàn)時期就是一名潛艇指揮官,被俘后在戰(zhàn)俘營想出了狼群戰(zhàn)術(shù)。狼群戰(zhàn)術(shù)主要核心就是當一艘潛艇發(fā)現(xiàn)目標后立即通知潛艇指揮部,把敵人的速度、航行、數(shù)量等情況說明。潛艇指揮部立即發(fā)報命令目標周圍的潛艇趕去支援和攻擊,這樣可以大大提高攻擊成功率,最大地殺傷敵人(潛艇多,攜帶的魚雷就多),減少己方的危險性。狼群戰(zhàn)術(shù)在二戰(zhàn)殘酷的海戰(zhàn)中證明是一種有效的戰(zhàn)術(shù),特別是鄧尼茨當上潛艇司令官后。如果不是美國在關(guān)鍵時候伸出援手支持了英國,很有可能英國就會被小小的潛艇打敗。丘吉爾在戰(zhàn)時對潛艇的一番評價最有說服力:“我們的脖子快被這些小家伙掐斷了!”

盟軍貨船被德國潛艇狼群戰(zhàn)術(shù)弄得苦不堪言,但海軍與空軍將領(lǐng)在很長的一段時間內(nèi)都拒絕改變他們的信條——小編制比大編制更安全,盡管有著鐵證證明這是錯誤的。Blackett證明了在一個有1 5～2 4艘船的艦隊中,每艘船有2.3%的概率被擊沉;而在艦隊船只數(shù)量高于4 5時,被擊中的概率只有1.1%。

欣賞完這兩則故事,也許大家對統(tǒng)計的重要作用有了初步的認識。那么,什么是統(tǒng)計呢?如果理解為動詞,就是對一系列的數(shù)據(jù)進行分析處理;如果理解為名詞,那可以簡單理解為統(tǒng)計學,統(tǒng)計學是一門具有方法論性質(zhì)的應(yīng)用性科學,它在概率論基礎(chǔ)上,發(fā)展出一系列的原理和方法,研究如何采集和整理反映事物總體信息的數(shù)字資料,并依據(jù)這些復(fù)雜的數(shù)據(jù)(稱為樣本)對總體的特征和現(xiàn)象背后隱藏的規(guī)律進行分析和推斷。

法國數(shù)學家拉普拉斯有句名言:“生活中最重要的問題,絕大部分其實只是概率問題。”我們看個具體例子,給定一根木棒,誰都不會懷疑它有自身的“客觀”的長度,長度是多少?我們可以用各種儀器去測量,但是不管我們的儀器多么精確,你得到的數(shù)據(jù)也總是穩(wěn)定在木棒真實長度的附近。事實上,我們?nèi)粘Ｖ胁痪褪前褱y量所得的值當作真實的“長度”而進行各類應(yīng)用嗎?

我們現(xiàn)在再來看看《普通高中數(shù)學課程標準(2 0 1 7年版)》對這部分內(nèi)容的要求:“數(shù)據(jù)收集和整理的方法、數(shù)據(jù)直觀圖表的表示方法、數(shù)據(jù)統(tǒng)計特征的刻畫方法”和“樣本相關(guān)系數(shù)的統(tǒng)計含義,了解一元線性回歸模型和2×2列聯(lián)表,運用這些方法解決簡單的實際問題”。從思想上來講,需要同學們“通過具體實例,感悟在實際生活中進行科學決策的必要性和可能性;體會統(tǒng)計思維與確定性思維的差異、歸納推斷與演繹證明的差異”。《普通高中數(shù)學課程標準(2 0 1 7年版)》對高中階段教學內(nèi)容進行這樣的要求,是有其歷史原因和現(xiàn)實背景的,下面我們就對其歷史進行簡單的梳理和介紹。

一、統(tǒng)計學的產(chǎn)生初期

統(tǒng)計學是隨著統(tǒng)計的產(chǎn)生而產(chǎn)生的,而統(tǒng)計作為一種社會實踐活動已有悠久的歷史。在中國,夏禹時代就有了人口數(shù)量的記載;為了賦稅、徭役和兵役的需要,歷代都有田畝和戶口等記錄。在國外,古巴比倫、埃及和羅馬帝國也有人口和資源的詳細記錄;到中世紀,西歐各國都有人口、軍隊、領(lǐng)地、職業(yè)、財產(chǎn)的統(tǒng)計。

比如被譽為古代數(shù)學“算經(jīng)十書”(漢唐之間出現(xiàn)的十部古算書)之首的《九章算術(shù)》就蘊涵著豐富的統(tǒng)計思想和統(tǒng)計理念。例如統(tǒng)計分組、線性擬合、抽樣推斷、加權(quán)平均等。

我國古代數(shù)學名著《九章算術(shù)》衰分章十七問為“生絲干耗”問題:“今有生絲三十斤,干之,耗三斤十二兩。今有干絲一十二斤,問生絲幾何。”

本題中以生絲三十得干絲過程損耗重量計算可得所謂“干絲率”,其實就是以此作為一個抽樣,并以該抽樣的平均數(shù)(即干、生絲的比值)來推斷總體,也就是所有生絲所能獲得干絲的比例,之后以該比例解決其他重量的生、干絲關(guān)系問題。暗含了以此個體數(shù)據(jù)作為整體通例數(shù)據(jù)的思想,抽樣推斷的痕跡十分明顯。

在應(yīng)用統(tǒng)計學進行抽樣的時候,問卷的設(shè)計是一門很大的學問。特別是對一些敏感性問題,即使調(diào)查是無記名的,也會使被調(diào)查者感到尷尬,從而使得結(jié)果與實際情況出入比較大。

這時候,我們就可以設(shè)計如下方案可使被調(diào)查者愿意作出真實的回答:在一個箱子里放進1個紅球和1個白球。被調(diào)查者在摸到球后記住顏色并立刻將球放回,然后根據(jù)球的顏色是紅和白分別回答如下問題:你的生日是不是奇數(shù)?你是否有過偷稅漏稅行為?回答時只要在一張預(yù)備好的白紙上寫下是或否。假定被調(diào)查者有2 0 0人,統(tǒng)計出共有5 8個是。

由題意可知,每個人從箱子中摸出1個白球或紅球的概率都是0.5,也就是我們期望大約有1 0 0個人回答了第一個問題,另1 0 0個人回答了第二個問題。在摸出紅球的情況下,答是的概率為0.5。因而大約有8個人回答了關(guān)于偷稅漏稅的問題。我們可以估計大約有8%的人有過偷稅漏稅行為。

上述問題的概率解釋為,已知P(紅)=0.5,P(是|紅)=0.5,P(是)=0.2 9,求條件概率P(是|白),用概率論中的貝葉斯公式算出的答案是8%。

二、統(tǒng)計學的發(fā)展時期

概率論起源于中世紀的歐洲,那時盛行擲骰子賭博,人們提出了許多有趣的概率問題。當時法國的帕斯卡、費爾馬和旅居巴黎的荷蘭數(shù)學家惠更斯都對此類問題感興趣,他們用組合數(shù)學研究了許多與擲骰子有關(guān)的概率計算問題。

概率論是統(tǒng)計推斷的基礎(chǔ),是在給定數(shù)據(jù)生成過程下觀測、研究數(shù)據(jù)的性質(zhì);而統(tǒng)計推斷則根據(jù)觀測的數(shù)據(jù),反向思考其數(shù)據(jù)生成過程。預(yù)測、分類、聚類、估計等,都是統(tǒng)計推斷的特殊形式,強調(diào)對于數(shù)據(jù)生成過程的研究。概率論大數(shù)定律的三個定理就是要說明為什么樣本均值可以估計總體均值,而這個估計的準確性卻是要由統(tǒng)計學說了算。對于各種分布的參數(shù)估計,之后的模擬估測,雖然與概率論看似完全無關(guān),實際上卻是由它們在支撐著統(tǒng)計學這個科目。這個情況對于參數(shù)統(tǒng)計、非參數(shù)統(tǒng)計、半?yún)?shù)統(tǒng)計,都是一樣的。

我們來看一個有關(guān)概率的案例——生日悖論:

眾所周知,在生活中,如果能夠遇到與自己同一天生日的人,我們大多會很驚喜,覺得這種緣分似乎很少見,又或者說這是一個很小的概率。那我們是否有想過,假如在2 3個人當中,出現(xiàn)兩個人是同一天生日的這種緣分的概率有多大呢?是5%?1 0%?還是2 0%?又或者是更多呢?下面我們一起來看看。

文章開始我們不想長篇大論地把很多公式給搬上來,那樣沒意思,吊足了大家的胃口,卻不受待見。所以,在開始的時候,我們就不打算寫那么多計算過程,留著后面慢慢討論和解釋。那么告訴各位:2 3個人中,有兩個人生日是同一天的概率約為5 0%(甚至比這個數(shù)值還高出那么一點點),在5 0個人中有相同生日的概率,竟然高達9 7%,這兩個數(shù)值,這兩個結(jié)果,各位是不是有點不太敢相信?

其實這個結(jié)果并沒有算錯,是有理有據(jù)的,只是我們的直覺錯了,科學與生活,就好比夢想和現(xiàn)實一樣:夢想往往是豐滿的,現(xiàn)實呢,卻常常是骨感的。正因為經(jīng)過科學方法計算出來的結(jié)果與我們?nèi)粘Ｉ畹慕?jīng)驗產(chǎn)生了如此大的落差,所以我們把這類問題稱為“生日悖論(B i r t h d a yP a r a d o x)”。

在分析時,我們不把某一年有2月2 9日或者某兩人是雙胞胎這樣的或者類似的外界因素算在內(nèi),只考慮純粹的隨機概率,也就是說每個人出生的日子都隨機分布在一年3 6 5天的任何一天。同時假設(shè)如果此時有n個人在同一房間內(nèi),要計算至少有兩個人生日是同一天的概率,假設(shè)一年3 6 5日出生概率是平均分布的(雖然在現(xiàn)實生活中,出生時間并不是平均分布的)。下面我們運用數(shù)學知識來慢慢解答和計算:

首先,假設(shè)P(n)代表n個人中每個人生日都不一樣的概率,前面說了,n不能大于3 6 5,故0≤n≤3 6 5,那么P(n)為:

第一個人的生日是3 6 5天的其中一天,假設(shè)是一定的,是不變的,那么第二個人不能跟第一個人有相同的生日的概率就是

理第三個人不能跟前兩個人生日相同,依此類推。很容易用階乘寫成如下形式

如果P(n)表示n個人中至少2人生日相同的概率,那么:

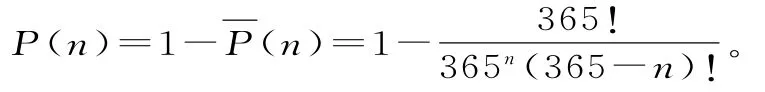
當n≥3 6 5時P(n)=1是必然的。當n=2 3時,代入公式得,概率大約是0.5 0 7。其,同他數(shù)字的概率用上面的算法可以近似地得出來,這里我們從網(wǎng)上下載了一張圖表(表1),我們可以大致感受下其變換過程:

表1

從上表可以看出,當n為4 1人是就已經(jīng)超過了9 0%,4 7人時就已經(jīng)超過了9 5%了。為什么實際情況與我們想象的差別這么大呢?我們把問題稍作改動,就能得到啟發(fā)。新的問題是:在一群人當中,有人與你同一天生日,這個概率有多大?仔細想想,這個問題還是比較簡單的。記p(n)表示房間中n個其他人中與特定人(比如你)有相同生日的概

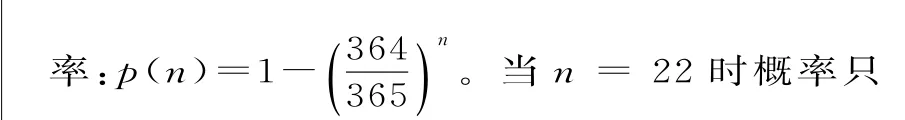
有大約0.0 5 9,約高于十七分之一。如果n個人中有5 0%概率存在某人跟你有相同生日,n至少要達到2 5 3,注意這個數(shù)字大大高于

所以,“生日悖論”產(chǎn)生的原因就是因為當我們看到“有人生日相同”時,下意識地用“與我生日相同”去推測,以至于把火箭發(fā)射當成了平穩(wěn)增長,造成了生日悖論。到了這里,大家是否對“生日悖論”有了更深一步的了解呢?所以生日悖論的本質(zhì)其實就是,隨著元素的增多,出現(xiàn)重復(fù)元素的概率會以驚人的速率增加,但是我們往往低估了它的速率。

三、統(tǒng)計學的成熟時期

2 0世紀初以來,科學技術(shù)迅猛發(fā)展,社會發(fā)生了巨大變化,統(tǒng)計學進入了快速發(fā)展時期。歸納起來有以下幾個方面。

由記述統(tǒng)計向推斷統(tǒng)計發(fā)展。記述統(tǒng)計是對所搜集的大量數(shù)據(jù)資料進行加工整理、綜合概括,通過圖示、列表和數(shù)字,如編制次數(shù)分布表、繪制直方圖、計算各種特征數(shù)等,對資料進行分析和描述。而推斷統(tǒng)計,則是在搜集、整理觀測的樣本數(shù)據(jù)基礎(chǔ)上,對有關(guān)總體作出推斷。其特點是根據(jù)帶隨機性的觀測樣本數(shù)據(jù)以及問題的條件和假定(模型),而對未知事物作出的,以概率形式表述的推斷。目前,西方國家所指的科學統(tǒng)計方法,主要就是指推斷統(tǒng)計來說的。但受到高中知識所限,我們現(xiàn)在所學內(nèi)容還只限于記述統(tǒng)計。

計算技術(shù)和一系列新技術(shù)、新方法在統(tǒng)計領(lǐng)域不斷得到開發(fā)和應(yīng)用。近幾十年,計算機技術(shù)不斷發(fā)展,使統(tǒng)計數(shù)據(jù)的搜集、處理、分析、存貯、傳遞、印制等過程日益現(xiàn)代化,提高了統(tǒng)計工作的效能。計算機技術(shù)的發(fā)展,日益擴大了傳統(tǒng)的和先進的統(tǒng)計技術(shù)的應(yīng)用領(lǐng)域,促使統(tǒng)計科學和統(tǒng)計工作發(fā)生了革命性的變化。如今,計算機科學已經(jīng)成為統(tǒng)計科學不可分割的組成部分。隨著科學技術(shù)的發(fā)展,統(tǒng)計理論、實踐深度和廣度方面也不斷發(fā)展。

受高中知識所限,我們不對最新統(tǒng)計知識進行介紹,而是再來欣賞三則統(tǒng)計悖論。

第一則案例——猜獎游戲:

這一問題出自美國的一個電視游戲節(jié)目,問題的名字來自該節(jié)目的主持人蒙提·霍爾。上世紀9 0年代曾在美國引起廣泛和熱烈的討論。

假定在臺上有三扇關(guān)閉的門,其中一扇門后面有一輛汽車,另外兩扇門后面各有一只山羊。主持人是知道哪扇門后面有汽車的。當競猜者選定了一扇門但尚未開啟它的時候,節(jié)目主持人去開啟剩下兩扇門中的一扇,露出的是山羊。主持人會問參賽者要不要改猜另一扇未開啟的門。

解決問題的關(guān)鍵是改猜另一扇未開啟的門是否比不改猜贏得汽車的概率要大。正確的答案是:改猜能增大贏得汽車的概率,從原來的1/3增大為2/3。這是因為競猜者選定的一扇門后面有汽車的概率是1/3,在未選定的兩扇門后面有汽車的概率是2/3,主持人開啟其中一扇門把這門后面有汽車給排除了,所以另一扇未開啟的門后面有汽車的概率是2/3。

第二則案例——“統(tǒng)計平均”的陷阱:

假定某大學數(shù)學系有教授1 5人、副教授4 0人、講師和助教2 5人,這三類人的平均年收入分別是1 5萬、1 2萬、8萬,該單位職工平均年收入為1 0萬。又假定科學院某研究所有研究員6 0人、副研究員3 0人、助研3 0人,這三類人的平均年收入分別是1 4萬、1 1萬、7萬,但該研究所職工平均年收入為1 1.5萬,高出那個系職工平均年收入1.5萬。這一例子表明:由于各單位人員構(gòu)成比例不同,單位職工平均年收入這一指標不能真實反映單位職工的收入狀況。

第三則案例——“辛普森悖論”:

看下面例子。假定有兩種藥(A和B),要通過分組臨床試驗對比其療效。表2是試驗結(jié)果的統(tǒng)計表。從甲乙兩組試驗結(jié)果看,藥物A的療效都優(yōu)于藥物B,但總體來看,藥物B的療效反而優(yōu)于藥物A(如表2所示)。

表2

早在2 0世紀初,人們就發(fā)現(xiàn)了這種現(xiàn)象:在分組比較中都占優(yōu)勢的一方,在總評中反而是失勢。直到1 9 5 1年英國統(tǒng)計學家辛普森在他發(fā)表的論文中才正式對這一現(xiàn)象給予理論解釋。后人就把這一現(xiàn)象稱為“辛普森悖論”。

理論上該如何解釋呢?

在最后總計A和B的治愈率時,實際上是對A和B治愈率按用藥率進行加權(quán)平均,即:

總計A的治愈率=甲組A的治愈率×甲組A的用藥率+乙組A的治愈率×乙組A的用藥率。

總計B的治愈率=甲組B的治愈率×甲組B的用藥率+乙組B的治愈率×乙組B的用藥率。

在這里的權(quán)數(shù)是用藥率。

按表2中所給數(shù)據(jù),具體算式是:

不難發(fā)現(xiàn),藥物A的療效都優(yōu)于藥物B,但總體來看,藥物B的療效反而優(yōu)于藥物A。可見,悖論的產(chǎn)生是由于“權(quán)重”的不同傾斜。在計算A的治愈率時,用藥率高的甲組的權(quán)重大,用藥率低的乙組的權(quán)重小;而在計算B的治愈率時,用藥率高的乙組的權(quán)重大,用藥率低的甲組的權(quán)重小。至于是什么原因引起權(quán)重的這種傾斜,則需要具體問題具體分析。

統(tǒng)計在現(xiàn)代化管理和社會生活中的地位日益重要。隨著社會、經(jīng)濟和科學技術(shù)的發(fā)展,統(tǒng)計在現(xiàn)代化國家管理和企業(yè)管理中的地位,在社會生活中的地位,越來越重要了。人們的日常生活和一切社會生活都離不開統(tǒng)計。英國統(tǒng)計學家哈斯利特說:“統(tǒng)計方法的應(yīng)用是這樣普遍,在我們的生活和習慣中,統(tǒng)計的影響是這樣巨大,以致統(tǒng)計的重要性無論怎樣強調(diào)也不過分。”甚至有的科學家還把我們的時代叫作“統(tǒng)計時代”。顯然,2 0世紀統(tǒng)計科學的發(fā)展及其未來,已經(jīng)被賦予了劃時代的意義。

事實上,統(tǒng)計學產(chǎn)生于應(yīng)用,在應(yīng)用過程中發(fā)展壯大。隨著經(jīng)濟社會的發(fā)展、各學科相互融合趨勢的發(fā)展和計算機技術(shù)的迅速發(fā)展,統(tǒng)計學的應(yīng)用領(lǐng)域、統(tǒng)計理論與分析方法也將不斷發(fā)展,在所有領(lǐng)域展現(xiàn)它的生命力和重要作用。