基于彈塑性耗能差率的地震損傷評估模型及分析方法

何浩祥， 陳 奎， 范少勇

(1．北京工業大學工程抗震與結構診治北京市重點實驗室， 北京 100124; 2．首都世界城市順暢交通北京市協同創新中心， 北京 100124)

引 言

地震動是復雜劇烈的隨機振動。在中震或大震作用下，建筑結構會發生不同程度的彈塑性損傷。傳統的結構抗震設計一般僅要求結構滿足規范規定的抗震設防目標，而基于性能的抗震設計則根據結構在地震中的不同性能需求確定更詳細的預定目標，從而實現社會對結構抗震性能的多層次要求[1]。在基于性能的抗震設計思想指導下，眾多研究者相繼提出了基于位移、基于能量、基于損傷和基于易損性等抗震設計方法以及相應的性能參數和目標[2]。

基于能量的抗震設計方法同時考慮了結構的承載能力和變形能力，更全面地反映了結構的抗震能力，因此相對更為綜合全面，是未來基于性能抗震設計方法中的重要組成。此外，地震對結構的作用是能量的傳遞、轉化與消耗的過程，良好的能量性能參數應既能充分反映地震動強度、頻譜、持時和加載路徑特性對結構累積損傷破壞的綜合影響，又能細致反映結構滯回耗能能力和延性特征。

Housner[3]首先提出結構的累積滯回耗能指標可以反映地震的累積損傷效應。之后，Akiyama[4]提出了基于能量抗震設計的思路和方法，并部分應用于日本抗震規范中。Fajfar[5]系統地研究了結構能量輸入和分配關系，使基于能量的抗震設計方法能夠綜合考慮滯回耗能與變形對結構損傷的影響。近年來，國內外學者在累積滯回耗能分布規律、輸入能量譜和累積滯回耗能譜以及基于能量的抗震設計體系與流程等方面進行了深入研究[6]。

縱觀現有成果，目前的基于能量的性能參數和抗震設計方法大多將結構等效為單自由度并利用能量譜分析來評價其性能，并沒有全面、充分地反映多維多自由度結構的能量需求和性能水平細節，同時在反映地震動時程下結構損傷過程、程度和隨機特性等方面也有所欠缺。鑒于此，在已有研究基礎上提出更加全面精確的能量參數和目標，細致表現構件、樓層和結構整體的損傷演變過程、性能水平與需求，具有重要的研究意義。

1 結構震害損傷評估模型述評

在基于性能的結構抗震設計體系內，震害損傷模型需要反映構件或結構在地震作用下的剛度、承載力和耗能能力退化的過程，即損傷演變過程。損傷指數是定量描述損傷模型特征的重要參數。現有的結構損傷模型分別包括基于強度、變形、剛度、周期(頻率)、能量和變形-能量雙重參數等多類。

基于變形的損傷模型一般將由能力譜法或時程分析法獲得的層間和頂部位移角作為損傷指數來評定結構的抗震性能，目前已成為性能設計中的常規方法。在推覆分析中，基于剛度的損傷模型得到了廣泛應用。在此基礎上，Ghobara[7]提出了以損傷前后兩次推覆分析獲得的剛度比來評價整體損傷的方法。但以上損傷模型均不能充分反映結構累積損傷特征和滯回耗能能力。HE[8]提出利用整體損傷指數、最大層間位移角、滯回耗能循環次數和樓層能量集中作為性能目標，建立了結構地震多重模糊損傷評估方法。近年來，通過時變周期(頻率)來評價結構整體動力損傷程度的方法逐漸興起[9]，但如何在動力分析中獲得更準確的時變特性以及如何考慮多階振型的影響仍需要深入研究。

一般認為，結構最大反應與累積耗能的損傷界限相互影響，因此在諸多損傷模型中由最大變形和累積滯回耗能線性組合而成的Park-Ang模型[10]被廣泛認可和應用，其公式為

(1)

式中xcu為構件在單調加載下的極限位移；Fy為構件的屈服強度；xm和Eh為構件實際的地震最大變形和累積滯變耗能；β為構件耗能因子。

然而，Park-Ang模型的不足也很明顯：(1)該模型采用的線性組合模式缺乏足夠的理論基礎，是一種半經驗模型，這種不準確性同樣表現在耗能因子的確定上；(2)一般僅適用于構件的靜動力損傷分析，在層間或結構整體的時程損傷分析中應用性較差；(3)界限值不嚴格收斂，在彈性階段其損傷指數不等于0，而在極限承載力階段損傷指數又通常大于1，嚴重影響了損傷評價精度；(4)不能反映加載中循環幅值變化對構件極限滯回耗能的影響，即加載路徑效應。針對上述問題，國內外學者對原始模型進行了不斷地修正，但并不能徹底改進所有缺陷[11-12]。

在基于能量的損傷模型中，Kr?tzig[13]提出了基于主從滯回環能量的模型，效果較好。Gosain,Krawinkler和Ibarra等分別提出基于循環退化率的損傷模型[14-16]。Kunnath[17]提出了結構滯回耗能循環次數的概念，即將結構總滯回耗能折算成結構在地震下經歷的最大滯回循環過程中消耗的能量的次數，用以反映結構滯回耗能能力。這些模型的共同不足是一般只限用于構件的低周往復損傷分析中，無法在結構整體的時程損傷分析中應用。另外，現有的基于能量譜的性能設計方法又通常偏重于簡單體系能量參數的概率特征和閾值控制而不能完全評價復雜結構的損傷細節。

有鑒于此，擺脫Park-Ang等損傷模型的形式束縛，探究結構在地震動下能量轉化消耗機理，不落窠臼地發展計算簡便準確、適用性強的動力損傷參數和模型具有重要的研究意義。

2 基于彈塑性耗能差率的損傷模型

2.1 彈塑性耗能差率損傷模型

在小幅外力作用下，構件或結構產生彈性變形能，此時若將該力撤去則結構可恢復到初始位移且不發生損傷。若外力作用較強，構件或結構將發生屈服破壞，轉化的能量以塑性變形能為主，且隨著力的增加產生更嚴重的損傷。如果提高結構的承載力令其不發生屈服，即確保結構處于理想彈性狀態，則損傷仍不會發生。可見，理想彈性變形能表征了結構保持彈性狀態需要消耗的變性能，而彈塑性變形能是結構實際產生的變性能。二者之間的差異越大，損傷越嚴重，因此該差值反映了損傷的形式和程度，即可以用該差值表征損傷特性。與上述思想類似，Najar[18]曾從能量損失的角度提出混凝土等脆性固體材料的損傷理論，認為損傷變量可用無損狀態下應變能與損傷狀態下應變能的差值與無損應變能之比來表示，該理論目前已在材料損傷評定和有限元分析中有所應用。

對于如圖1所示的理想彈塑性單自由度體系，設其彈性階段的剛度為ke，后屈服剛度系數為α，屈服力和屈服位移分別為Fy和uy。當結構處于彈塑性狀態時，在位移um處的力和位移分別為Fm和um，現時延性為μm=um/uy，相應的周期為Tm。假定彈塑性狀態時的結構可采用割線剛度km進行等效，則

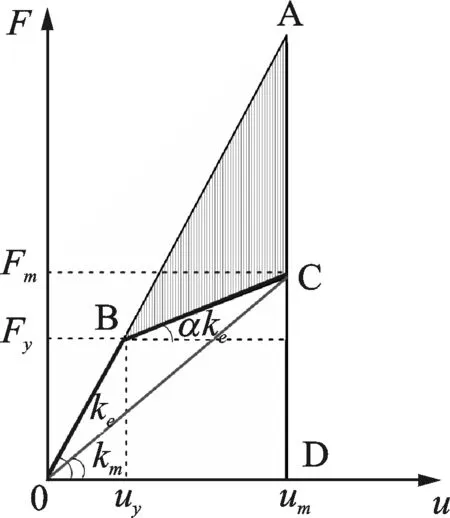
圖1 理想彈塑性體系耗能示意圖
Fig.1 Energy dissipation of ideal elastic-plastic system

其剛度損傷指數可表示為

(2)

如圖1所示，面積S0BCD為結構位移為um時實際產生的彈塑性變形能EF，面積S0AD為相應的結構理想彈性變形能EE，面積SABC為上述二者之差，即彈塑性耗能差ED。由以上概念提出的基于彈塑性耗能差率的損傷指數可表示為

(3)

由以上結果可以看出，該能量損傷指數與剛度損傷指數均能夠反映結構恢復力特征、最大彈塑性變形、延性和周期等重要因素，且形式近似。二者的區別在于前者反映了現時延性變化的平方趨勢，而后者反映了現時延性變化的線性特征，分別符合各自的理論框架。綜上可認為：基于能量、剛度、位移和周期的損傷模型是密切相關的，表征形式相關聯但內涵不同。剛度損傷指數由于近似等效產生了一定程度的偏差，而能量損傷指數的概念則更嚴格、明確和全面，數值嚴格在0～1之間，是構建最理想的損傷模型的基礎。

2.2 擬靜力下的耗能差率損傷模型

對于在低周往復加載等擬靜力作用下的結構，一般認為可采用累積滯回耗能或體系變形能來準確描述加載過程中產生的累積損傷程度。由于基于彈塑性耗能差率的損傷模型涉及恢復力特征和位移響應，能夠明確地反映包含累積滯回耗在內的體系變形能與理想彈性變形能之間的關系，因此在對單調加載的損傷模型基礎上進行一定改進后，可以使其適用于擬靜力加載下的損傷評估。

設i為加載歷程中第i個加載步驟，且結構或構件在外力F(i)下已進入彈塑性階段，利用試驗技術或彈塑性分析方法可獲得結構的基底剪力FF(i)和頂部位移uF(i)，則相應加載步下結構整體的等效彈塑性變形能可表示為EF(i)=0.5FF(i)uF(i)。在全部結果中，該彈塑性體系頂部位移最大值為uFMax。若將外力作用F(i)乘以降幅系數γ以確保結構在外力γF(i)作用下只產生彈性變形，且其頂部位移結果及其最大值分別為uE0(i)和uE0MAX，其基底剪力結果為FE0(i)。設調幅系數β=uFMAX/uE0MAX，則為了使結構頂部彈性最大位移能夠達到uFMax，需要將uE0(i)乘以β倍得到調幅彈性位移uE(i)=βuE0(i)，相應的調幅彈性力為FE(i)=βFE0(i)。因此，根據本文提出的基于理想彈性變形能差的損傷模型的思想，對應于外力F(i)下的結構等效理想彈性變形能可表示為

EE(i)=0.5FE(i)uE(i)=

0.5β2FE0(i)uE0(i)

(4)

由此可推導出對于在外力F(t)下已進入彈塑性狀態的結構能量損傷指數曲線可表示為

(5)

式中FFi和FEi分別為第i步驟時彈塑性狀態下和理想彈性狀態下的基底剪力，uFi和uEi分別為第i步驟時彈塑性狀態下和理想彈性狀態下的頂部位移。

2.3 動力下的耗能差率損傷模型

對于彈塑性單自由度體系，其在地震動作用下的結構動力方程為

(6)

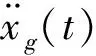
將上式兩端對相對位移x取從x(0)到x(t0)積分，可得

EK(t)+ED(t)+EF(t)=EI(t)

(7)

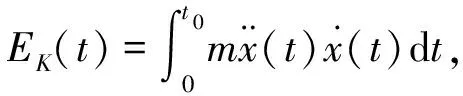
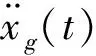
EE(t)=FE(t)uE(t)=β2FE0(t)uE0(t)

(8)

(9)

式中FFi和FEi分別為i時刻彈塑性狀態下和理想彈性狀態下的基底剪力，uFi和uEi分別為i時刻彈塑性狀態下和理想彈性狀態下的頂部位移,b為結構首次進入屈服狀態時對應的時間點，n為從時間點b至現時t的步長數。只有準確確定b值方能確保在地震動初始階段結構尚處于彈性狀態時其能量損傷指數為0。建議按下述方法確定b值：分別計算等效彈塑性剛度時程kF(t)=FF(t)/uF(t)和等效彈性剛度時程kE0(t)=FE0(t)/uE0(t)，然后計算等效剛度比時程R(t)=kE0(t)/kF(t)。當R(t)首次出現明顯大于1的時間點即可取為b。

基于理想彈性變形能差的損傷指數曲線能夠準確反映結構恢復力特征、累積滯回耗能時變性和損傷演變過程，且其值嚴格控制在0～1之間。通常可取損傷指數曲線中的最大值或末段中較穩定的數值作為等效損傷值。此外，通過對不同記錄和幅值的地震動下的響應進行分析，還可以得到結構的易損性曲線。值得注意的是，在個別大震下結構的頂部位移最大值出現的時刻可能與中小震下位移最大值出現的時刻tp不同，為確保損傷指數的一致性，建議將大震時程里tp時刻對應的位移作為有效最大值uFMax。

針對基于性能的結構設計框架，根據震后結構的破壞程度和修復水平，可將震害劃分為基本完好、輕微破壞、中等破壞、嚴重破壞和倒塌5個等級。參考已有研究成果并結合能量損傷指數的特點，定義對應結構不同破壞等級的損傷性能目標，如表1所示。通過式(5)或(9)和表1便可較便捷地實現結構整體或其在某一方向的損傷評估。

表1 不同震害等級對應的損傷指標范圍

Tab.1 Range of damage index for different damage grades

損傷程度破壞描述損傷目標基本完好承重構件完好,個別非承重構件輕微損壞,附屬構件有不同程度破壞。0.00～0.10輕微損傷個別承重構件有輕微殘余變形,個別非結構構件明顯破壞,附屬構件有不同程度破壞。0.10～0.25中等破壞多數承重構件有輕微殘余變形,部分有明顯殘余變形,個別非結構構件嚴重破壞。0.25～0.60嚴重破壞多數承重構件嚴重破壞或部分倒塌0.60～0.80倒塌多數承重構件倒塌。0.80～1.00

2.4 不同損傷模型能力比較

需要指出的是，已有部分研究者提出了利用結構理想彈性耗能和實際累積耗能之間的聯系建立損傷模型和指數的方法。劉哲鋒等[19]將結構損傷定義為結構在單向水平荷載作用下結構耗散塑性應變能與存儲彈性應變能的能力的損失，并構建損傷模型，但該方法并不能體現結構滯回耗能的演變過程。劉良林等[20]將釋放的彈性能與理想彈性能之比定義為構件損傷指標，沒有反映滯回耗能對損傷的影響，其結果是不正確的。刁波等[21]基于能量耗散原理和滯回特性建立了構件累積損傷模型，其形式與本文提出的靜力作用下的能量損傷模型類似，但未能解決真實地震動下結構的時變損傷的求解問題。本文提出的方法機理明確、閾值嚴格，且對靜動力下的構件和結構損傷評定均能適用。表2比較了前文所述不同類型的損傷模型或損傷評定方法的特點和能力。其中，“機理明確”是指相應的計算公式是否有明確的力學基礎。可以看出，本文提出的損傷模型具有較強的優勢，可以進一步應用和發展。

表2 不同損傷模型能力比較

注：●表示具備相應能力，○表示不具備相應能力；“/”表示或者。

3 算例分析

為了驗證能量損傷模型在構件和結構損傷評定中的準確性和全面性，本文針對不同結構類型和加載模式進行計算分析。首先，利用文[22]中的剪力墻低周反復試驗盲賽數據及Opensees有限元模型，驗證能量損傷模型在構件不同靜力加載模式下的準確性。該剪力墻模型尺寸及配筋如圖2所示。對剪力墻頂端進行位移單調加載，通過有限元模擬獲得其反力-位移曲線和損傷指數曲線如圖3所示。結果表明損傷指數能夠準確反映該模型損傷逐漸發展直至倒塌破壞的過程。

采用數值分析方法， 對剪力墻頂端施加力并采用位移控制，進行如圖4所示的兩種不同路徑下的低周往復加載。相關滯回曲線如圖5所示。提取每一加載循環下的滯回環曲線，并按照式(1)計算出Park-Ang損傷指數曲線，按照式(5)計算基于彈塑性耗能差率的能量損傷指數曲線，結果如圖6和7所示。可以看出，兩種模型都在一定程度上體現了剪力墻的損傷發展規律，但Park-Ang損傷指數過早地超過了1，同時也不能充分表征不同加載路徑下損傷演變的差異。究其原因， Park-Ang損傷模型中能量損傷項的分母為常數，而分子部分表示的累積滯變耗能將隨著滯回環的增加不斷增大。因此，其值實際表示了滯回耗能的增長趨勢而沒有充分表征損傷的演變特性；此外，由于該值并不是能量的相對變化率，因而其最大值很可能超過損傷閾值上限1。與此相反，能量損傷指數克服了上述局限。此外，如圖7所示，在加載路徑2中結構在初始階段出現明顯大變形之后又恢復正常，因此其損傷指數出現了激增和突變。此現象驗證了損傷指數能夠反映不同加載路徑下的損傷演變，且其具體數值和變化規律更準確細致。

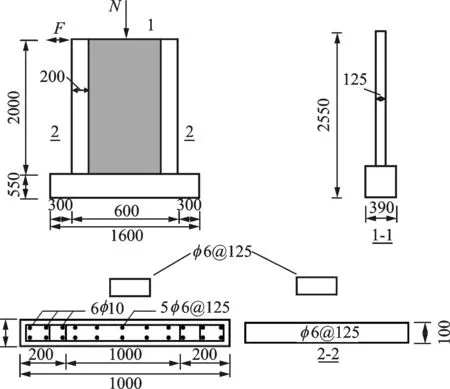
圖2 剪力墻模型簡圖(單位:mm)Fig.2 Shear wall fiber model diagram(Unit:mm)

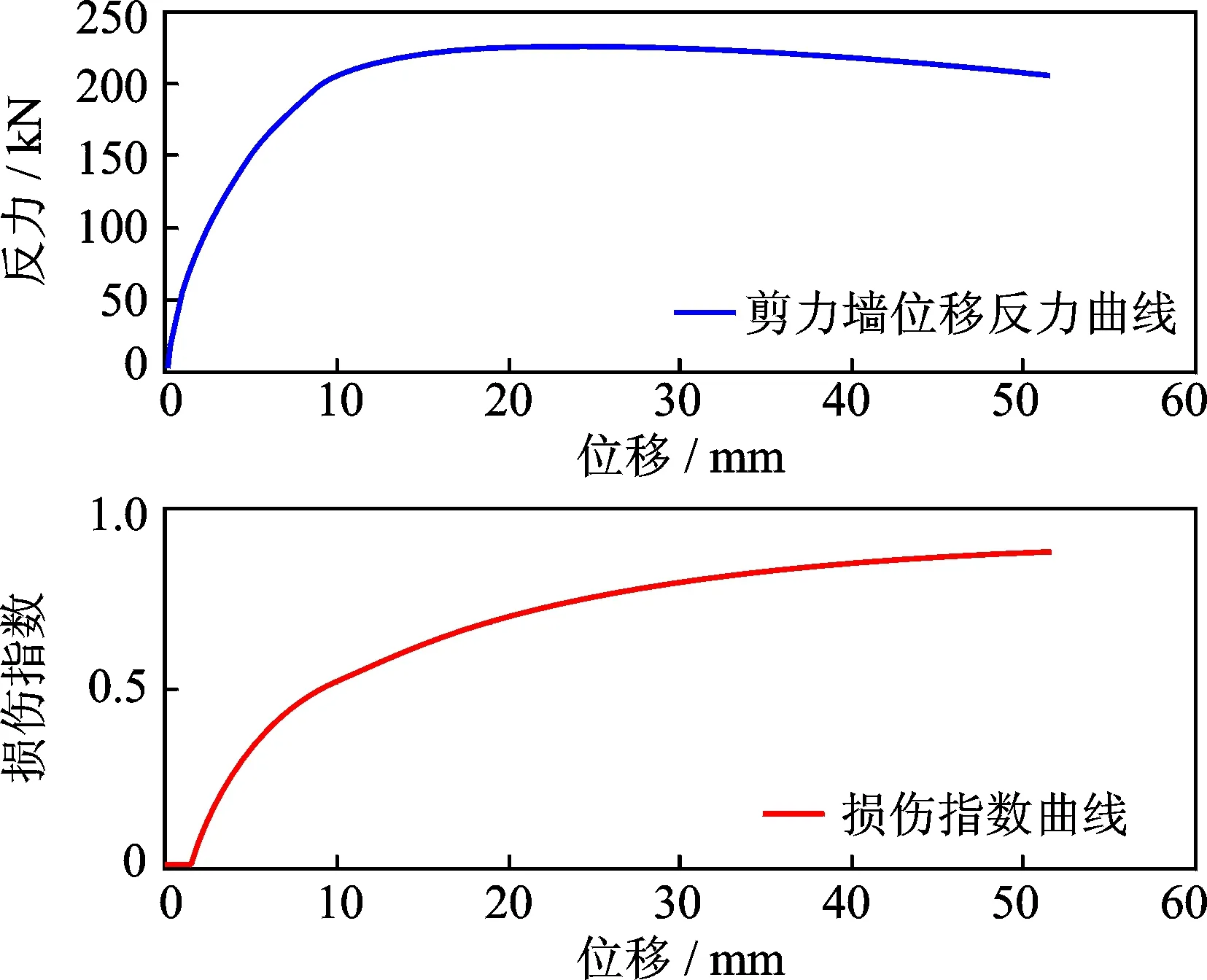
圖3 剪力墻反力-位移曲線與損傷曲線Fig.3 Force-displacement curve and damage curve

圖4 不同低周往復加載路徑對比Fig.4 Comparison of different load paths

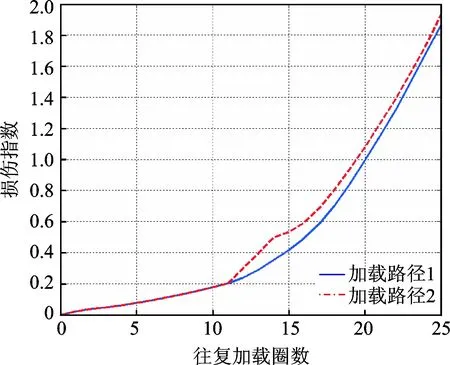
圖6 不同加載路徑下Park-Ang損傷指數對比Fig.6 Park-Ang index of different load paths

圖7 不同加載路徑下能量損傷指數對比
Fig.7 Energy damage index under different load paths

為了驗證能量損傷模型同樣適用于結構的推覆分析和地震動時程分析，本文建立如圖8所示的6層框架結構有限元模型并利用Opensees進行計算。該結構底層層高3.5 m，其余層高3 m，X向和Y向長度分別為9 m和7 m。柱截面尺寸為400 mm×400 mm，配筋率為1.5%，梁截面尺寸為200 mm×200 mm，配筋率為1.2%。鋼筋采用HRB400，混凝土等級為C35。首先分別采用倒三角和均布加載模式對結構進行推覆分析。對結構頂部進行位移控制，目標位移為200 mm。提取底部剪力和頂部節點位移，如圖9所示，計算得到結構的能量損傷曲線，如圖10所示。結合圖9和10可見隨著頂部位移的增加，結構損傷呈遞增趨勢，直到發生嚴重破壞后損傷指數變化緩慢。可認為基于能量的損傷模型能夠準確反映推覆模式下的結構損傷發展過程。

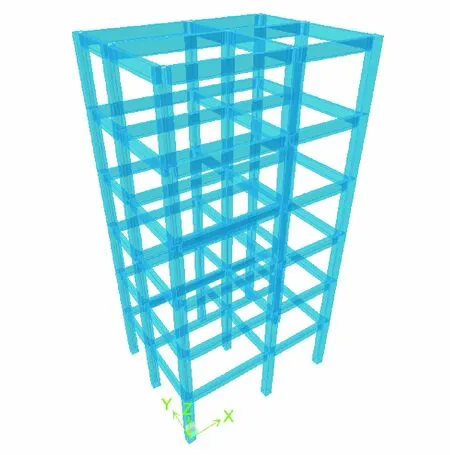
圖8 框架結構示意圖
Fig.8 Schematic diagram of RC frame

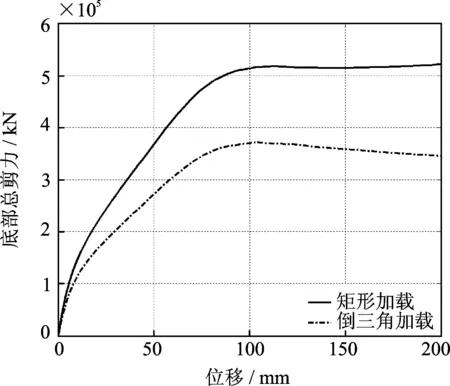
圖9 不同推覆加載模式下頂部位移與基底剪力曲線
Fig.9 Top displacement and base shear of pushover modes

圖10 不同推覆加載模式下結構損傷曲線Fig.10 Damage index of different pushover modes

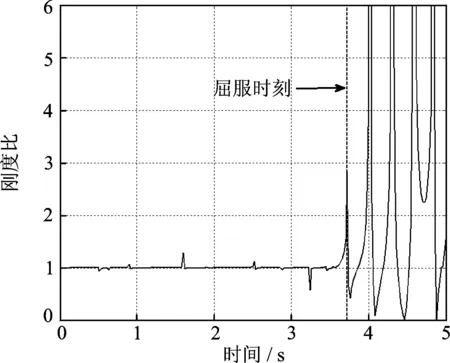
圖11 等效剛度比曲線Fig.11 Effective stiffness ratio curve

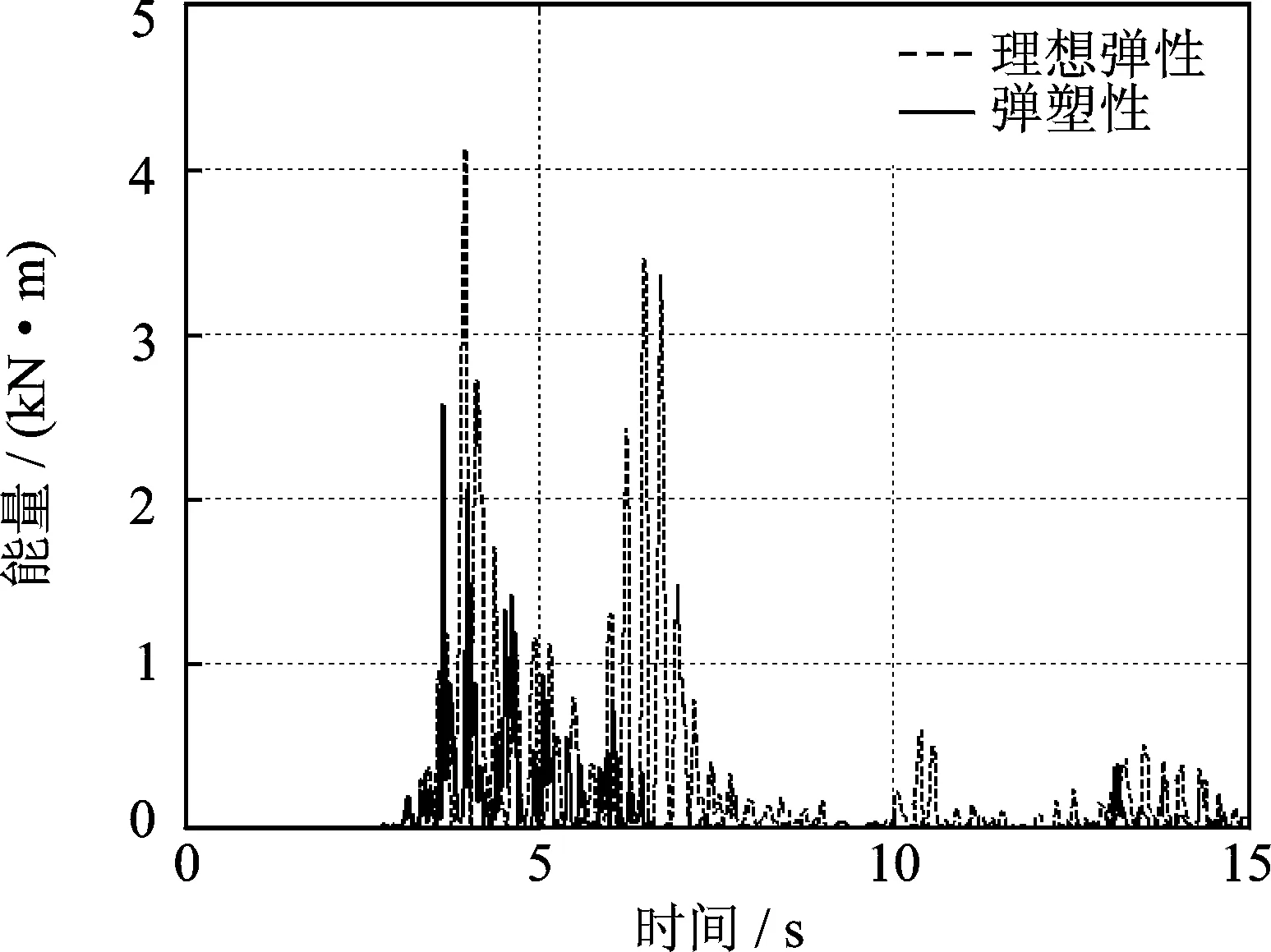
圖12 彈性與彈塑性瞬時能量對比Fig.12 Comparison of instantaneous energy

采用彈塑性動力時程分析計算單向和三向El Centro波作用下該框架結構的動力響應，分析其在地震下的整體損傷和層間損傷演變規律，結果如圖11～14所示。按上文所述方法計算等效剛度比時程R(t)，發現在3.8 s左右剛度比已明顯超過1.0，因此將該時刻確定為初始屈服時刻。結構整體的等效彈塑性變形能EF(t)和理想彈性變形能EE(t)曲線如圖12所示，可見在3～7 s持時內是結構主要發生彈塑性耗能的階段，在時程中后期EE(t)已明顯大于EF(t)，結構損傷趨于平穩。

從圖12可以看出，當結構整體一旦屈服后，能量損傷指數隨著地震動的幅值逐漸增大迅速增長，其數值隨著地震動和響應的隨機性和往復性發生一定的波動，且嚴格介于0～1之間。在地震后期由于地震動幅值的逐漸減少以及結構自身剛度的恢復，損傷指數呈現適當的下降。在中小震下，結構的損傷發展較緩慢，并且損傷峰值相對于地震峰值有滯后性；在大震下，結構迅速發生明顯的嚴重損傷，損傷指數峰值和地震峰值基本同步。此外，比較圖13和14的結果可以發現能量損傷指數較明顯地反映了地震動多維耦合作用對損傷發展的不利影響。

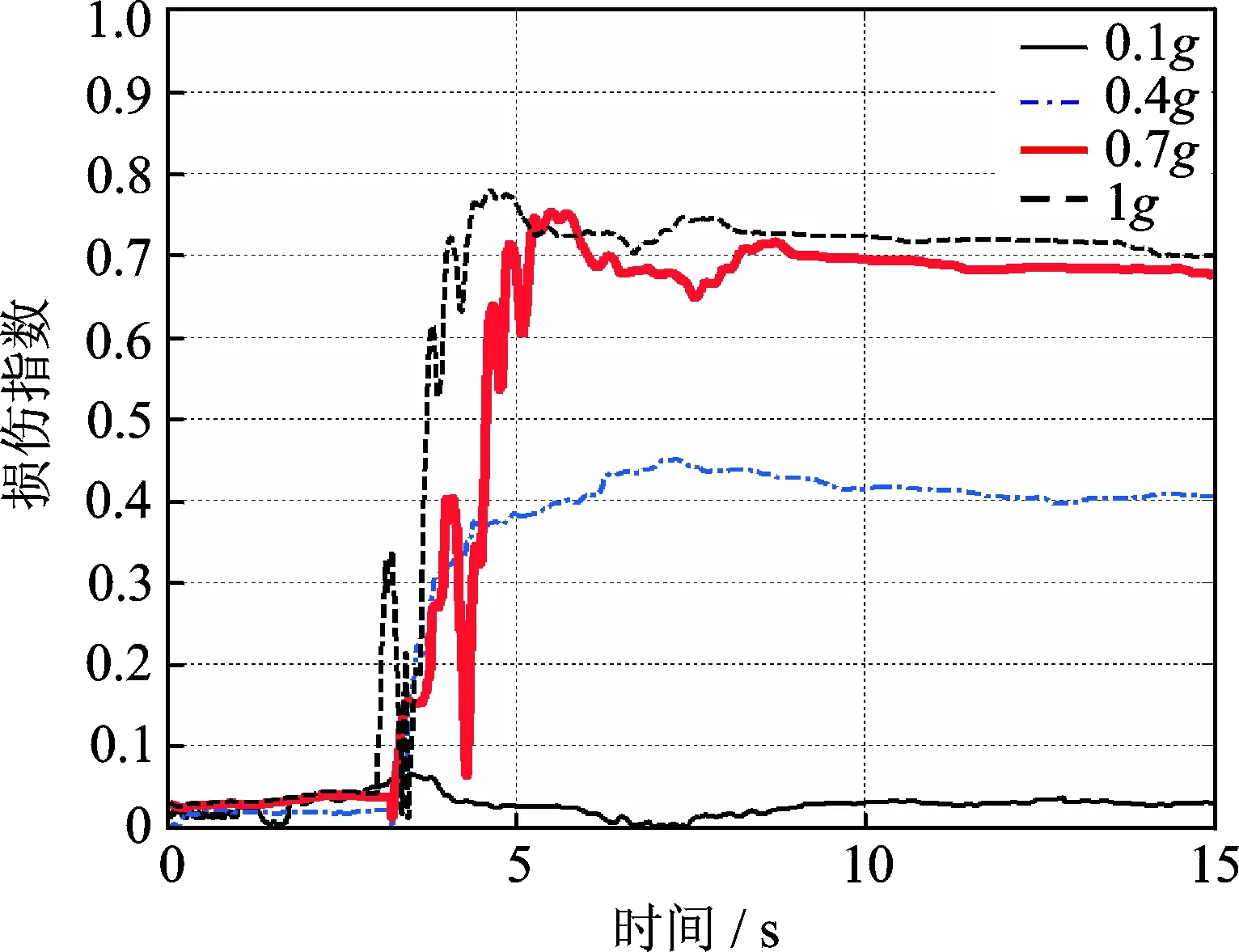
圖13 單向地震下不同地震幅值損傷曲線對比Fig.13 Damage curves of single direction earthquakes

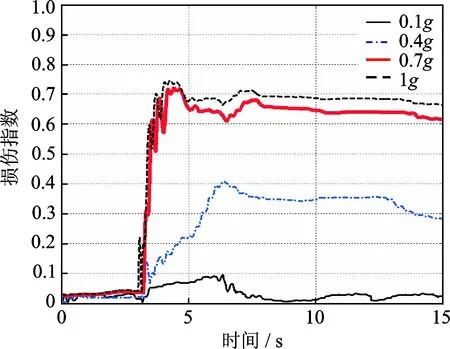
圖14 多維地震下不同地震幅值損傷曲線對比Fig.14 Damage curves of multiple earthquakes

利用各樓層的層間剪力和層間位移可獲得各層的損傷指數最大值和最大層間位移，其中0.7g地震下的結果如圖15所示，可以看出底層的損傷最為嚴重，隨著層數的增加，損傷不斷減小，這符合結構的實際情況。同時也可發現僅僅依靠層間位移來判斷各層損傷程度是不夠準確全面的。

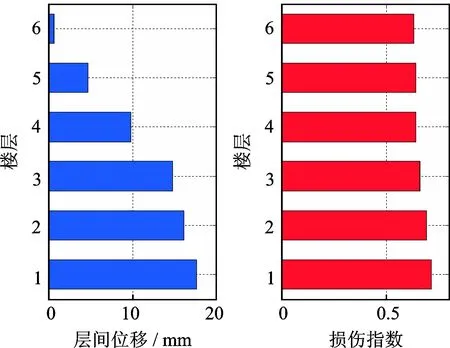
圖15 層間損傷曲線對比Fig.15 Comparison of floor damage curves

綜上所述，本文提出的基于能量差的損傷模型能夠準確、全面、細致地表征構件和結構在靜力加載和地震動作用下的損傷演變過程和特征，可為基于性能的結構抗震設計的應用和發展提供有力的支持。

4 結 論

結構在地震作用下的損傷演變過程是復雜隨機的。在材料、構件、整體結構3個層次上建立良好的損傷模型和損傷指數反映損傷狀態，不僅能夠準確有效地評價結構損傷的變化和程度，還可以為基于性能的結構設計和修復提供必要的依據。目前的損傷模型和損傷指數類型眾多，但大部分存在諸如機理不明確、閾值范圍不嚴格、無法反映不同層次下的結構加載路徑和耦合作用等不足，制約了基于性能的結構設計的發展和普及。結構地震損傷破壞是由地震動特性和結構耗能特性共同決定的，基于能量的損傷模型機理明確，能夠全面反映地震動和結構能量傳遞、轉化與消耗的過程并對損傷程度做出準確判斷。

本文認為損傷的形式和程度與結構理想彈性變形能和實際彈塑性變形能之間的差異直接相關，可以用該差值表征損傷。針對目前各種損傷模型的不足，進而提出了對應不同靜動力加載方式的彈塑性耗能差損傷模型。從靜力和動力兩個角度分別闡述了相關能量模型的機理以及其與基于其他參數損傷模型之間的聯系與區別，論證了該模型的優越性。提出了利用彈塑性動力時程分析方法獲得基底剪力和頂部位移從而計算理想彈性變形能、整體屈服產生時刻，進而獲得結構損傷演變過程的方法。最后，通過剪力墻及框架結構靜動力彈塑性分析驗證了該能量損傷模型具有機理明確、閾值嚴格、計算準確便捷、適用性強以及能夠同時反映加載路徑效應和多維耦合作用影響等優點，可以應用和推廣。

[1] ATC-58. Guidelines for seismic performance assessment of buildings [S]. Washington DC: Applied Technology Council, 2009.

[2] Mihai M. A theoretical review of the damage indices used to model the dynamic nonlinear behavior of reinforced concrete structures [J]. Bulletin of the Polytechnic Institute of Iasi, 2013, 63(2): 109—119.

[3] Housner G W. Behavior of structures during earthquake [J]. Journal of the Engineering Mechanics Division,ASCE, 1959, 85(4): 109—129.

[4] Akiyama H. Earthquake Resistant Limit State Design for Buildings [M]. University of Tokyo Press, 1985.

[5] Fajfar P, Vidic T. Consistent inelastic design spectra hysteretic and input energy [J]. Earthquake Engineering and Structural Dynamics, 1994, 23(5): 523—537.

[6] 葉列平, 繆志偉, 程光煜,等. 建筑結構基于能量抗震設計方法研究[J]. 工程力學, 2014, 31(6): 1—12.

Ye Lieping, Miao Zhiwei, Cheng Guangyu, et al. Study on the energy-based seismic design method of building structures [J]. Engineering Mechanics, 2014, 31(6): 1—12.

[7] Ghobarah A, Abou-Elfath H, Biddah A. Response based damage assessment of structures [J]. Earthquake Engineering and Structural Dynamics, 1999, 28(1): 29—104.

[8] HE Hao-xiang, CONG Mao-lin, Lü Yong-wei. Earthquake damage assessment for RC structures based on fuzzy sets [J]. Mathematical Problems in Engineering, 2013, (22): Article ID 254865.

[9] Dipasquale E, Ju J W, Askar A, et al. Relation between global damage indices and local stiffness degradation [J]. Journal of Structural Engineering, ASCE, 1990, 116(5): 1440—1456.

[10] Park Y, Ang A H S. Mechanistic seismic damage model for reinforced concrete [J]. Journal of Structural Engineering, ASCE, 1985, 111(4): 722—739.

[11] 付 國, 劉伯權, 邢國華. 基于有效耗能的改進Park-Ang 雙參數損傷模型計算研究[J]. 工程力學, 2013,30(8): 84—90.

Fu Guo, Liu Boquan, Xing Guohua. The research and calculation on modified Park-Ang double parameter seismic damage model based on energy dissipation [J]. Engineering Mechanics, 2013, 30(8): 84—90.

[12] 羅文文, 李英民, 韓 軍. 考慮加載路徑影響的改進Park-Ang損傷模型 [J]. 工程力學, 2014, 31(7): 112—118.

Luo Wenwen, Li Yingmin, Han Jun. A modified park-ang seismic damage model considering the load path effects [J]. Engineering Mechanics, 2014, 31(7): 112—118.

[13] Kr?tzig W B, Meyer I F, Meskouris K. Damage evolution in reinforced concrete members under cyclic loading [C]. Proceedings of 5th International Conference on Structural Safety and Reliability, San Francisco, 1989: 795—802.

[14] Gosain N K, Brown R H, Jirsa J O. Shear requirement for load reversals on RC members [J]. Journal of Structural Engineering, 1977, 103(7): 1461—1476.

[15] Krawinkler H, Zohrei M. Cumulative damage in steel structures subjected to earthquake ground motion [J]. Computers and Structures, 1983, 16 (14): 531—541.

[16] Ibarra L F, Medina R A, Krawinkler H. Hysteretic models that incorporate strength and stiffness deterioration [J]. Earthquake Engineering and Structural Dynamics, 2005, 34(12): 1489—1511.

[17] Kunnath S K, Chai Y H. Cumulative damage-based inelastic cyclic demand spectrum [J]. Earthquake Engineering and Structural Dynamics, 2004, 33(3): 499—520.

[18] Krajcinovic D, Lemaitre J. Continuum Damage Mechanics Theory and Applications [M]. New York: Springer Verilag, 1987: 233—294.

[19] 劉哲鋒, 周 瓊, 陳 逵. 基于能量耗儲能力的結構地震損傷量化研究[J]. 工程力學, 2013, 30(2): 169—173.

Liu Zhefeng, Zhou Qiong, Chen Kui. Quantitative analysis of seismic damage based on structural energy dissipation and storage capability [J]. Engineering Mechanics, 2013, 30(2): 169—173.

[20] 劉良林, 王全鳳, 梁愛民. 基于彈性能的結構地震損傷評價方法[J]. 桂林理工大學學報, 2014, 34(3): 479—483.

Liu Lianglin, Wang Quanfeng, Liang Aimin. Method of structure seismic damage evaluation based on elastic energy [J]. Journal of Guilin University of Technology, 2014, 34(3): 479—483.

[21] 刁 波, 李淑春, 葉英華. 反復荷載作用下混凝土異形柱結構累積損傷分析及試驗研究[J]. 建筑結構學報, 2008, 29(1): 57—63.

Diao Bo, Li Shuchun, Ye Yinghua. Analysis and experiment of cumulated damage of RC structures with special columns under cyclic loading [J]. Journal of Building Structures, 2008, 29(1): 57—63.

[22] Lu Xinzheng, Xie Linlin, Guan Hong, et al. A shear wall element for nonlinear seismic analysis of super-tall buildings using OpenSees [J]. Finite Elements in Analysis and Design, 2015, 98(1): 14—25.