基于理性思維發展的高中數學課堂教學研究

☉江蘇省常熟市梅李高級中學 孫 長

數學是一門邏輯性很強的理科.那么，我們如何在教學中滲透這個“理”呢？筆者認為在平時的教學中應該關注理性思維的發展.筆者曾有幸聽了一節以理性思維發展為主線的數學公開課，下面結合具體的教學簡錄，談一談筆者的思考.

一、教學過程簡錄

1.知識準備

引題：已知集合A={x|x2-3x+2=0}和B={x|x-1=0}，判斷A、B之間的關系.

學生：由A={1，2}，B={1}知，B是A的真子集.

2.學以致用

例1 已知集合A={x|x2-3x+2=0}與B={x|ax+1=0，x∈R}，若B?A，求實數a的值.

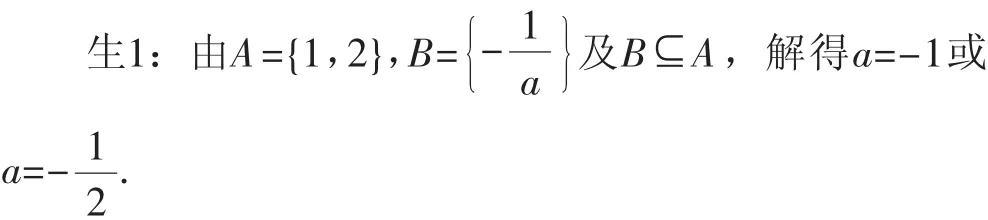
師：這是類比引題中的思路所作出的解題過程，生1首先用列舉法表示了集合A、B，然后又結合B?A這一條件最終得出了a的值，方法看上去一點沒有錯誤，但就是有一點問題，問題在哪里呢？

生2：a≠0……

很多學生產生疑惑：a≠0，但結果沒有0呢……

師：a=0是一種特殊情況，大家想到用哪個方式可以判斷呢？

生3：代入法.當a=0時，0·x+1=0沒有實數解，即B=?，符合題意.

師（板書解題過程）：運用單個數值進行單獨處理的思路很不錯.那剛開始怎么會把a=0遺漏掉的呢？

生：解方程ax+1=0的時候將系數a除掉了.

師：很好.ax+1=0看上去像一次方程，事實上，當a≠0時，它是的；但是，當a=0時，它就不是了.因此，我們在解題時不能想當然地用除以a來求解.所以，我們解題時應進行理性的思考并準確把握研究對象的本質屬性，輕易被某種形式迷惑后解題思路就會很容易產生偏差.

評注：質疑是學習者進行理性思考時最為突出的表現，因此，教師在教學中面對學生錯誤時不要簡單修正，應該引導學生質疑并及時發現自己的思維缺陷，質疑、發現錯誤、自主修正的過程能夠很好地培養學生的求真意識.其次，思考a=0是否可行并不能僅憑讀題時的感覺來判斷，運用代入檢測這一數學方法進行確認的過程才是最求真務實的.

3.思維鍛造

變式1：已知集合A={x|x2-3x+2=0}與B={x|x2-2x+2a-1=0，x∈R}，若B?A，求實數a的值.

生1：A={1，2}，

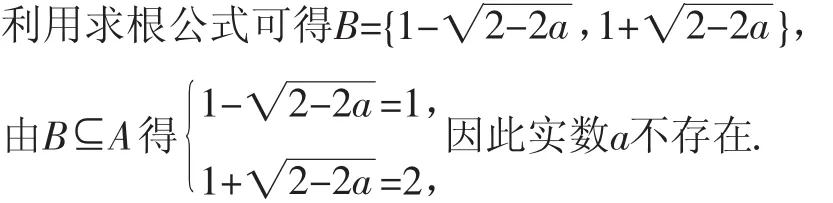
師：此題無解，同學們有意見嗎？

生2：不對，有解的.

由題意可知，B=?，{1}，{2}，{1，2}. 當B=?時，Δ=4-8a+4＜0，即a＞1；當B={1}時，由根與系數的關系可得2a-1=1，即a=1；當B={2}時，實數a不存在；當B={1，2}時，實數a不存在.因此，a≥1.

師：分情況討論并逐一驗證討論猜想才是最有依據、最可靠的，大家體會到利用求根公式求解的錯誤了嗎？

生：求根公式在Δ＜0時不能用.師：當Δ＜0時，B=?，即a＞1；

師：很好.大家再看此題：已知一個含有n個元素的集合有2n個子集，如果我們將條件中的“集合A={x|x2-3x+2=0}”改成“集合A={1，2，3}”，那么集合B又有多少種可能呢？

生（個別）：8種，7種.

生（笑）：有很多.

師：子集的數量會隨著元素的增多而“猛增”，因此進行逐一討論自然是不夠現實可行的，那么大家可有更好的方法來減少討論的情況呢？回顧例1，能根據“A={1，2}，B?A”這一條件來斷定集合B中元素的大概取值嗎？

生：只能取到1、2.

師：很好，也就是說B=?或1∈B或2∈B，這樣能解得結果嗎？

生3：當B=?時，Δ=4-8a+4＜0，

即a＞1；當1∈B時，2a-2=0，

即a=1，此時B={1}?A；當2∈B時，2a-1=0，

綜上所述，a≥1.

師：很好，根據這一解題思路來考慮，集合A中元素再多也沒有關系.

評注：引導學生探求各種辦法來解題的過程將求真、求簡、求新的數學精神完全展現了出來.學生利用求根公式求解實數根時展現了其思維的片面性而導致結果產生錯誤，教師引導學生質疑與剖析錯誤的過程是促使學生逐步體驗求真務實精神的滲透教學.教師在學生正確解題之后又及時引導學生換角度思考問題并獲得更加簡潔而新穎的解法，學生的研究意識、求簡求新的理性精神在這一過程中也就得到了很好的培養與鍛煉.

練習：已知集合A={x|x2-3x+2=0}與B={x|x2-2ax+2a-1=0，x∈R}，若B?A，求實數a的值.

生1：A={1，2}，當B=?時，

Δ=4a2-8a+4=4（a-1）2＜0，無解；

當1∈B時，1-2a+2a-1=0恒成立，

即a∈R；

當2∈R時，4-4a+2a-1=0，

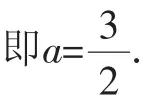
綜上所述，a∈R.

師：“a∈R”這一條件告訴我們所有的實數a都是滿足題意的，大家以為呢？

生2：a=0就不行.

師：能夠找到反例就說明解題肯定有問題，那么問題究竟出在哪里了呢？

生3：x2-2ax+2a-1=0能因式分解，兩根為x=1，x=2a-1，B={1，2a-1}.因此a=1或

評注：在學生初步掌握本類問題解題方法之際及時布置練習能夠很好地幫助學生鞏固、辨析知識，這也正是數學學習理性精神應該展現的地方.學生在鞏固練習中也明白了數學問題的解決常常有通法與特法的存在，學生在實際問題的解決中應根據題意進行靈活的選擇，“解無定法”的理性精神也在這一過程中得到了有意義的滲透.

4.沉淀結晶

變式2：已知集合A={x|x2-3x+2=0}與B={x|x2-2ax+m=0，x∈R}，如果B≠?且B?A，求實數a，m的值.

生1：A={1，2}，當1∈B時，1-2a+m=0；當2∈B時，4-4a+m=0.（再往后就解不下去了）

師：這一解題思路是存在著一定的道理的，那么聯立方程組又代表了怎樣的含義呢？

生：方程聯立表示1∈B和2∈B是同時成立的.

師：是不是只有B={1，2}呢？

生：不是.

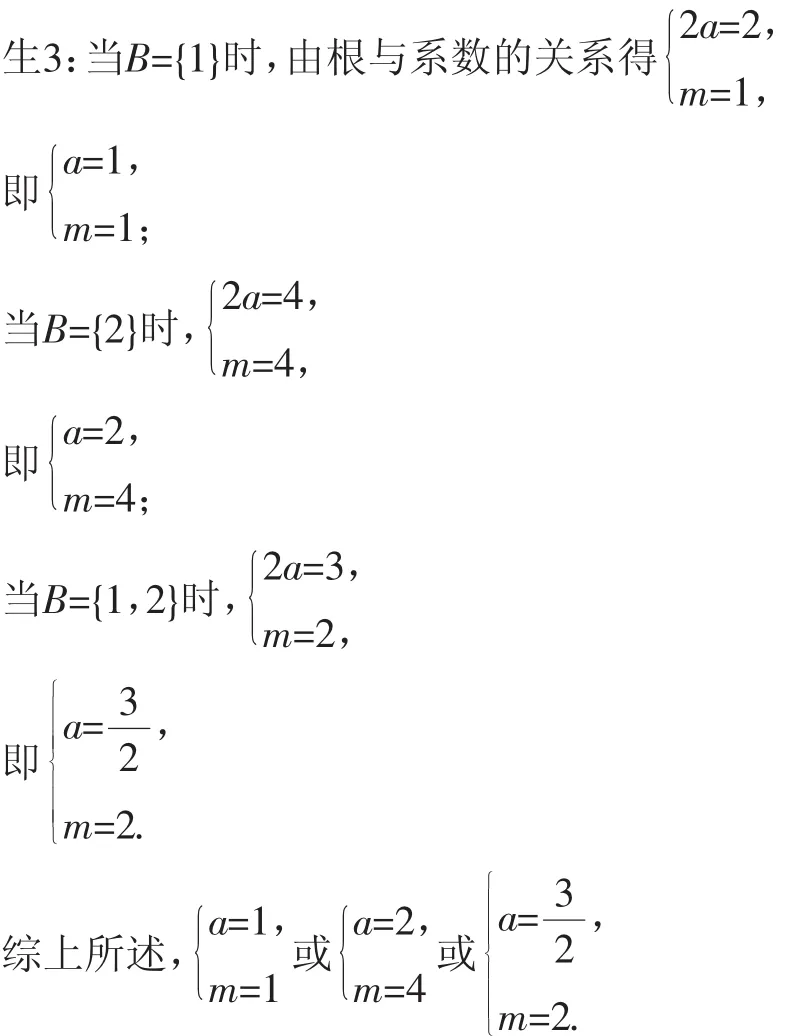
師：很好，變式1中的第二種解題方法在這里又得到了很好的運用，這可真是峰回路轉啊.

最后教師再引導學生從上述集合的包含關系的問題中進行思考與總結，最終得出解決此類問題的基本思路.

評注：含有兩個字母參數的一元二次方程的求解比之前的題目相對更有難度，學生從集合B的元素角度對問題展開思考并得到了一個無法求解的二元一次方程，這時候看上去已經無法繼續解題，聯立二元一次方程組成了唯一可以繼續的路，最終得到a，m的一組數值，這充分表現出高一新生經常憑感覺做運算而欠缺理性精神.

二、筆者的些許思考

事實上，剛剛步入高中的學生最不能適應的往往就是數學的學習，導致高一學生數學學習不適應的原因有很多，其中最為重要的兩個因素為：①高一學生尚未建立高中數學學習的良好思維方式與學習習慣，對于高一數學所涉及的解題策略、表達格式與能力目標等各方面內容也知之甚少；②集合知識的高度抽象性令學生在數學學習中時常感覺困難重重.

以集合的包含關系為載體的本課教學強調了集合的兩種表示方式，列舉法與描述法這兩種表示方式之間的轉化使得數學對象具體和抽象的特征得到了清晰的刻畫和體現，辯證的思想也得到了很好的滲透；元素和集合的關系在解題的過程中得到了靈活的運用，個體和整體的意識也在解題的過程中得以滲透；由易到難的集合包含關系的變式將數學研究求真、求新的過程展現得淋漓盡致.學生自主學習的習慣與理性思維的方式都在這樣的教學過程中得到了有意義的培養，不僅如此，學生對最優解題策略的探索、解題與表達格式的規范等環節也都能在這樣的教學中一一達成.

由此可見，高中學生在數學學習中理性精神的培養具有可操作性，教師在實際教學中應理性選擇、利用教學內容進行滲透理性精神的教學，理性教學策略與方法的合理運用一定能夠保障數學教學的實在效果.