巧妙轉化 靈活變通
——從“化歸法”專題習題課說起

☉江蘇省常熟市尚湖高級中學 孫 丹

“化歸”即轉化，是在分析、解決數學問題的時候采用某種數學方法對問題進行變換，使之轉化進而達到解決的一種方法.實際上，化歸思想已經滲透到了高中數學內容的方方面面，數學離不開化歸思想，比如將未知量向已知量轉化，現實問題向數學模型轉化，復雜問題向簡單問題轉化等.可以說，化歸思想是解決數學問題的有效方法，也是一種應用極廣的數學思維方式.

最近，筆者聽了一高三習題課，主題就是“化歸與轉化”.授課老師結合一系列的練習題向學生講解了這一思想方法的常用情形，引導學生認識與掌握這一思想方法.個人認為教學效果顯著，現從以下幾點進行論述.

適用情形一：追本溯源，復雜函數簡化處理

【教師】同學們，高中階段我們學習的函數很多，有反比例函數、一次函數、二次函數、指數函數、對數函數等，這些基本的函數類型就是大家處理復雜函數的題根，題根能給我們的解答過程提供化歸的方向.因此，同學們在遇到一些復合函數時可以嘗試將其向題根轉化，變成初等函數，問題也就迎刃而解了.下面我們以具體的練習進行說明.

【案例展示】已知f（x）=cos2x-sinx，求函數f（x）的值域.

【教師提問】同學們，拿到這道題，大家有什么思路？

【學生甲】f（x）涉及到了正弦函數與余弦函數，首先需要統一，可以把cos2x轉化為1-2sin2x，函數f（x）也就變成了-2sin2x-sinx+1.

【教師提問】沒錯，這是比較合理的處理方法，之后要怎么求解函數f（x）的值域呢？直接用三角函數的內容？

【學生乙】可以換元處理，令a=sinx，原函數也就變成了f（a）=-2a2-a+1，根據三角函數的值域可以知道a的取值范圍為［-1，1］.二次函數值域的求解就很容易了，結合圖像（如圖1）我們就知道值域為

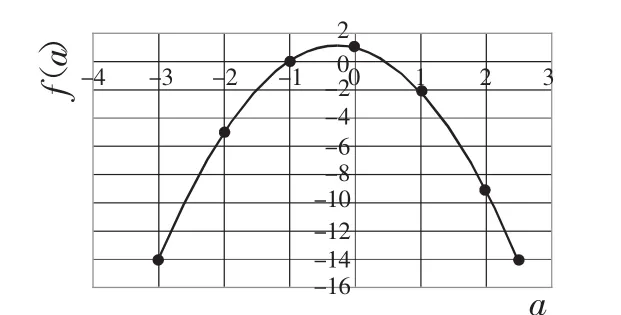
圖1

【評析】二次型函數、高次函數等都是常考題型，這些函數看起來形式復雜，難度很大，其實歸根結底就是對二次函數的考察，只要進行一定的轉化處理，進行變量代換，明確新的變量的取值范圍，結合二次函數的相關性質，問題很容易解決.

適用情形二：不等式轉化為函數

不等式是高中數學的重要內容，也是高考的必考內容.對于不等式的考查往往不會局限在這個單一的知識點上，而是與其他內容相結合，形成更為復雜的綜合題，這些綜合題對學生的解題方法、思維、能力的要求更高.解題時，學生需要將題目還原成一個個知識點，逐步解決，這個過程也是“化歸思想”的體現.下面以不等式轉化為函數為例進行說明.

【案例展示】已知x的取值范圍為［-1，2］時，不等式a≥x2-2x-1恒成立，求實數a的取值范圍.

【教師提問】在x的取值范圍內，a≥x2-2x-1恒成立，這個條件說明了什么？

【學生甲】無論x取什么值，a都要比x2-2x-1取到的值大.

【教師提問】怎么把這個條件轉化成數學語言呢？

【學生乙】在x∈［-1，2］的范圍內，a大于等于x2-2x-1的最大值.

【教師提問】沒錯，這么一來，這道不等式問題就轉化成了函數問題.哪位同學在黑板上解答一下.

【學生丙板書】設f（x）=x2-2x-1=（x-1）2-2，

因為x的取值范圍為［-1，2］，

所以在x=-1時，f（x）max=2，

所以a∈［2，+∞）.

【評析】不等式反映的是不同變量之間的相互制約關系，是一種變量之間的內在聯系.不等式與函數的單調性、有界性等性質之間具有較強的聯系，因此在處理不等式時將其轉化為函數問題是一種合理并且有效的解決方法.

適用情形三：立體幾何代數化

【案例展示】已知：在三棱柱ABCA1B1C1中，AA1C1C是一個正方形，邊長為4，與面ABC相垂直.AB=3，BC=5.

求解：二面角A1-BC1-B1的余弦值是多少？

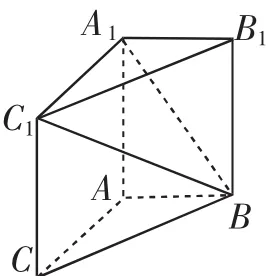
圖2

【教師提問】在解決這個問題前，同學們先思考一下，怎樣求解二面角？

【學生甲】作兩個面交線的垂線，構造三角形.

【教師提問】那這道題用常規方法可以做嗎？

【學生甲】有點麻煩，做出來我也不知道對不對.

【教師提問】考試時，答題之前同學們要認真審題，看清每個已知條件，看已知條件滿不滿足你們選用的方法.這道題如果選用常規方法，計算量顯然太大，解答過程也不嚴謹，很容易會扣過程分.我給同學們提供一個思路，在平面幾何中，遇到計算題我們會建立平面坐標系，借助向量進行運算，那么這里應該怎么處理？

【學生乙】建立空間坐標系，用空間向量算.

【教師提問】那乙同學你上來解答一下.

【學生乙板書】由AC2+AB2=BC2，

得AB⊥AC.

又面AA1C1C⊥面ABC，

A1A⊥AC，

所以A1A⊥AB.

所以A1（0，0，4），B（0，3，0），

圖3

設平面A1BC1的法向量為m=（x1，y1，z1），平面B1BC1的法向量為n=（x2，y2，z2）

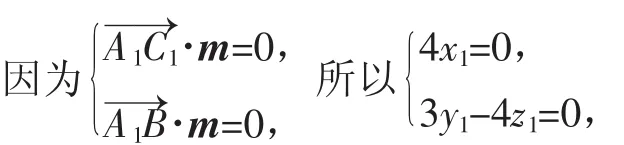
令m=（0，4，3）.

【評析】在解決幾何中的計算時，借助向量運算的手段能使得解題過程更為清晰準確.可以說，向量是用代數方法解決幾何問題最有效的方法.在立體幾何中也是這樣，只要建立起適當的空間坐標系，那么立體幾何中的所有運算都可以轉化為代數問題進行解決.

適用情形四：定點定值轉化為恒等式

在高中數學內容體系中，解析幾何是教學的重點，也是難點.以圓錐曲線為例，對于這一部分的知識內容，相當一部分學生不能理解圓錐曲線相關內容所蘊含的數學思想以及數學方法，拿到題目就是套公式進行計算，而不是仔細審題，聯系其他知識點進行轉化.許多同學在解決圓錐曲線計算題時都會遇到計算量巨大的問題，有同學表示算到最后不知道自己算的是什么，式子越算越復雜，就是求不出結果.下面以具體教學案例為說明.

【教師提問】同學們，在解決解析幾何問題時，大家要養成將已知條件量化的習慣，尋找題目表達出來的各種數量關系.哪位同學來說一下題目中能提煉出哪些數量關系？

【學生】根據題干信息可以知道A點的坐標為（-a，0），F的坐標為（-c，0）.P為圓O上的動點，設其為（x，y）.假設=u，所以有關系式：

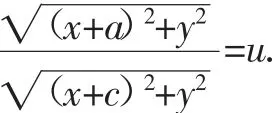
因為P在圓O：x2+y2=b2上，

所以滿足a2+b2-u2（b2+c2）+（2a-2u2c）x=0，

【教師提問】你繼續算下去，看能不能得到最終結果.

【評析】在高考中，有關圓錐曲線計算結果恒為定值或者圖形恒過定點是常考題型，這類題目如果用常規方法進行計算是很復雜的，顯然命題人考核的重點并不是計算，而是數學思想的應用.因此，同學們要熟練掌握化歸的思想方法，善于把這類問題轉化為關于某個變量的恒等式問題，進而簡化代數運算.

這節習題課后，筆者認識到“化歸”這一思想方法能有效實現由實際問題向數學問題、復雜問題向簡單問題、陌生問題向熟悉問題等的轉化.當然，要做到這種變通，就需要學生具備較強的解題能力，而解題能力的關鍵就是基礎理論知識.因此在日常的教學過程中，教師要強化基礎訓練，引導學生掌握好常規的思維方法.在這個基礎上引導學生進行化歸思維方法訓練，做到舉一反三，觸類旁通，提升數學解題能力.J