一題一世界
——一次說題的實(shí)踐和思考

☉江蘇省江安高級(jí)中學(xué) 黃建鋒

說題是數(shù)學(xué)教研活動(dòng)的一種重要載體，相比以往的解題，說題更為深刻地反映了對試題的理解、知識(shí)的運(yùn)用，更為本質(zhì)地思考以及深入研究后續(xù)考查點(diǎn).可以這么說，說題形態(tài)漸漸成為各地教育主管部門考查教師的重要形式.如何說題呢？筆者以為從多個(gè)方面進(jìn)行思考：首先，說解法；其次，說規(guī)律；最后，說思想和本質(zhì).

問題：非零向量a，b滿足|a|=|b|=a·b=2，且（a-c）·（b-2c）=0，求|b-c|最小值.

一、說解法

本題是向量綜合性問題，需要從綜合性角度思考.試想，向量問題的主要入手方向是什么？根據(jù)向量的兩要素——長度和方向，其入手方向自然是代數(shù)和幾何.因此可以從不同的角度去探索基本解法.

解法1：不少學(xué)生對于向量的學(xué)習(xí)基本處在一維思維模式狀態(tài)，即用“一維”數(shù)的眼光在看待“二維”向量的問題，因此其往往不可避免地陷入運(yùn)算之中，即代數(shù)法的運(yùn)用.不能說代數(shù)法不好，只是代數(shù)法在解決綜合性問題時(shí)其優(yōu)勢相對較少.比如，學(xué)生往往喜歡這樣解決：出發(fā)，利用（b-c）的構(gòu)造，即0=（a-c）·

這是自由向量的構(gòu)造，前提是整體性思想較為突出，并且對自由向量數(shù)量積運(yùn)算有一定的要求.

解法2：不難發(fā)現(xiàn)，本題給出的兩個(gè)向量滿足夾角是60°，且模長已經(jīng)給定，因此學(xué)生頭腦中對其有更為簡捷的代數(shù)方式——坐標(biāo)向量，這是很多學(xué)生喜歡的向量求解方式.如圖1，建立直角坐標(biāo)系，設(shè)=c=（x，y），得a-c=（2-x，-y），b-2c=（1-2x，-2y），由（a-c）·（b-2c）=0，得（2-x）（1-2x）+（-y）（

圖1

|b-c|2=.坐標(biāo)法簡單易操作，更注重向量代數(shù)性的工具，需要扎實(shí)的運(yùn)算能力以及各種知識(shí)的綜合性運(yùn)用能力.

圖2

解法3：從向量另一重要特性出發(fā)，其必有幾何解法.對條件分析可知，向量a，b滿足夾角60°，問題就圍繞向量a，b，c建構(gòu)圖形解決.如圖2，設(shè)a-c.由題意可知即∠ACD=90°，則點(diǎn)C的軌跡是以Q為圓心，以AD為直徑的圓上的點(diǎn).又|b-c|=||，問題轉(zhuǎn)化為定點(diǎn)B與圓上動(dòng)點(diǎn)C的最值.至此，問題已到達(dá)學(xué)生能認(rèn)知的模式，|b-c|最小值為BQ-r.給出計(jì)從圖形結(jié)構(gòu)的角度入手，顯然是對向量條件的圖形化構(gòu)造，這里垂直關(guān)系往往要結(jié)合平面幾何中圓的相關(guān)知識(shí)，利用向量幾何特征解決問題更有思維意義，也是考試命題的重要方向.

二、說規(guī)律

近年來，向量在中學(xué)數(shù)學(xué)中的地位愈來愈重要，向量問題的考查難度也在逐步加深，學(xué)生對向量的理解、教師對向量的教學(xué)難度也在不斷上升，因此要通過問題將向量教學(xué)呈現(xiàn)出一定的規(guī)律性，從而獲得向量教學(xué)更好的方式.

從向量在中學(xué)數(shù)學(xué)中的內(nèi)容來看，其知識(shí)點(diǎn)主要呈現(xiàn)在：向量的概念—向量的加減法—向量的數(shù)乘—向量基本定理—數(shù)量積.在學(xué)習(xí)過程中呈現(xiàn)規(guī)律性的始終是兩點(diǎn)：代數(shù)的運(yùn)算方式或者幾何圖形的建構(gòu)方式.這兩點(diǎn)既是問題的本質(zhì)所在，又體現(xiàn)了向量工具性的特征.從幾何圖形的角度來說，向量教學(xué)的規(guī)律主要是挖掘平面幾何的意義，這也是問題解決的關(guān)鍵，將平面幾何與向量幾何特征緊密聯(lián)系起來，問題的解決便是水到渠成的事.

變式1：非零向量a≠e，|e|=1，對任意t∈R，恒有|ate|≥|a-e|，則e·（a-e）=______.

圖3

規(guī)律：從幾何角度來說，這樣的問題往往涉及平面幾何中最基本的一個(gè)知識(shí)——“點(diǎn)到直線的距離垂線段最短”，若沒有結(jié)合圖形思考，學(xué)生往往通過代數(shù)的大量運(yùn)算求解.從圖3來看，不難發(fā)現(xiàn)垂線段最短這一幾何規(guī)律，顯然e⊥（a-e），因此數(shù)量積為0.類似的問題數(shù)不勝數(shù).如果從代數(shù)規(guī)律中尋找，勢必離不開一定的運(yùn)算：由|a-te|≥|a-e|，兩邊平方，得t2-2（a·e）t+2a·e-1≥0，對任意t∈R恒成立，只要Δ=4（a·e）2-4（2a·e-1）≤0即可，所以Δ=4（a·e）2-4（2a·e-1）=4［（a·e）2-2a·e+1）］=4［（a·e-1）2］≤0，得（a·e-1）2≤0?a·e=1，顯然此時(shí)的e·（a-e）=e·a-e2=0.

變式2： 設(shè)e1，e2為單位向量，非零向量b=xe1+ye2，x，

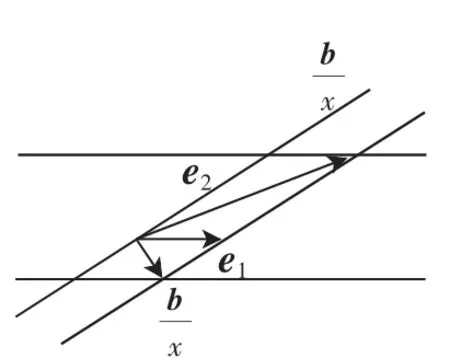
圖4

規(guī)律：將問題稍加改變，思考“點(diǎn)到直線的距離垂線段最短”如何運(yùn)用.不妨設(shè)x≠0，結(jié)合平行四邊形法則（如圖4），的最大值為2.問題依舊在尋找?guī)缀我?guī)律——垂線段最短，盡管有干擾元素x、y，但是其問題的規(guī)律性依舊，當(dāng)然本題也可以從代數(shù)規(guī)律思考：b2=|b|2=（xe1+ye2）2=x2+y2+的最大值為2.

這里的兩道變式題說的是問題的統(tǒng)一規(guī)律，即找到幾何特征的規(guī)律，與本文中的原題相比，筆者認(rèn)為幾何特征的規(guī)律性更為重要一些，尋找問題的共性是說題的根本所在，也是近年來考試命題的方向所在，其比代數(shù)運(yùn)算更重要.

三、說思想

向量問題解決的數(shù)學(xué)思想是什么？筆者以為主要是一個(gè)思想方法，即數(shù)形結(jié)合思想.數(shù)形結(jié)合思想在向量中的運(yùn)用有兩層含義，其一是以數(shù)解形，再者是以形輔數(shù).向量試題恰恰是兩方面的重要反映，緊緊抓住數(shù)形結(jié)合思想這兩方面的立意，對于向量問題的解決有著重要作用.

圖5

思路2：可以從＜a-c，b-c＞=60°及數(shù)量積出發(fā)，利用基本不等式求|c|的最值.由題意|a+b|=1，由（a-c）·（b-c）=結(jié)合上述兩式：a·b-（a+b）·c+|c2|≤［1-（a+b）·c+|c|2］，化簡，得|c|2≤2+（a+b）·c≤2+|a+b·||c|=2+|c|，得|c|2-|c|-2≤0?|c|≤2，即最大模長為2.

我們發(fā)現(xiàn)，向量問題的解決離不開數(shù)形結(jié)合思想，本文從問題開始到變式，以及改編，始終圍繞數(shù)形結(jié)合思想的兩條主線進(jìn)行：以數(shù)如何解形？以形如何輔數(shù)？在說題過程中，至始至終圍繞明確的數(shù)學(xué)思想將問題呈現(xiàn)出來，是說題的基本思想，另一方面我們要將向量問題的本質(zhì)領(lǐng)會(huì)清楚：即向量問題的解法本質(zhì)在于找到合適的圖形建構(gòu)或者是代數(shù)化的機(jī)械運(yùn)算，這兩大本質(zhì)特性成為向量工具性最好的詮釋.

說題是一個(gè)重要的教學(xué)形態(tài)，是教師不斷優(yōu)化問題解法的重要方式，筆者以為教師要提升自身綜合素養(yǎng)、提升自身的解題水平，多參與這樣的說題嘗試，對于教師專業(yè)化的提升有重要的幫助.一個(gè)題就是多個(gè)知識(shí)點(diǎn)的整合，說好一個(gè)題，勢必要厘清各種知識(shí)的內(nèi)在聯(lián)系以及整理解決問題的規(guī)律性的東西，摸索其背后的數(shù)學(xué)思想方法，甚至還能融會(huì)貫通的改編一些原創(chuàng)問題，長此以往就能獲得“一個(gè)世界”，正所謂一題一世界，知識(shí)相連接.