一道雙變元最值題的多思維角度剖析

☉山東省泰安第一中學 李曉楠

在近年的高考題與模擬題中，經常會碰到求解雙變元或多變元的代數式的最值或取值范圍問題.此類問題往往難度較大，思維方式多變，方法有時也多樣.多做題不如精做題，當我們解完一道題以后，要不斷領悟反思，多角度切入進行深度挖掘，以求達到觸類旁通、一題多解的效果.下面結合一道雙變元代數式的最值題來加以實例剖析，多角度切入，來體會其異曲同工之妙.

【問題】已知實數x，y滿足x2+2xy-1=0，則x2+y2的最小值為______.

分析：這是一道雙變元在已知條件下求其代數式的最值問題，這類問題一直受備命題者的青睞.通過認真審視這道題，在不同視角下，得到了該題的不同解題思維與對應的精彩解法.

思維角度1：結合已知關系式進行因式分解，通過對關系式x+2y進行換元，得到x、y關于新參數的關系式，代入所要求解的代數式，通過變形，利用基本不等式進行求解.對已知等式進行因式分解，采用換元法，可以簡化運算，提升效益.

思維角度2：結合已知關系式得到x2+2xy=1，通過基本不等式法的轉化，并結合所要求解的結果進行對比系數得到關系式1+=t，求解參數t的值并代入不等式，通過不等式的性質來轉化即可確定對應的最值問題.

解法2（基本不等式法）：由于x2+2xy-1=0，則有x2+2xy=1，結合基本不等式有1=x2+2xy≤x2+x2+ty（2其中參數t＞0），當且僅當x2=ty2時，等號成立，結合系數關系

思維角度3：結合已知關系式得到x2+2xy=1，設x2+y2=t（t＞0），進而建立關系式x2+y2=t（x2+2xy），轉化為關于x的一元二次方程，利用函數與方程，結合判別式來確定最值問題.

解法3（二次方程法）：由于x2+2xy-1=0，則有x2+2xy=1，設x2+y2=t（t＞0），則有x2+y2=t（x2+2xy），整理有（1-t）x2-2tyx+y2=0，由以上關于x的一元二次方程有實數根，可得1-t≠0且Δ=4t2y2-4（1-t）y2≥0，整理有t2+t-1≥0，解得t≥

思維角度4：結合已知關系式得到x2+2xy=1，通過代數式x2+y2的除“1”轉化為分式，結合參數t=的引入，通過轉化相應的分式，結合基本不等式來確定相應的最值問題.

思維角度5：根據所要求解的代數式的形式進行三角換元x=rcosα，y=rsinα，代入已知關系式并分離參數r，結合三角恒等變換，并利用三角函數的圖像與性質來確定相應的最值問題即可.

解法5（三角換元法）：由于x2+2xy-1=0，則有x2+2xy=1，設x=rcosα，y=rsinα，則有r2cos2α+2r2sinαcosα=1，整理可

思維角度6：結合已知關系式得到x2+2xy=1，設出x2+y2=r2，進而結合三角換元思維代入關系式1=x2+2xy，通過三角恒等變換，并利用三角函數的圖像與性質來確定相應的最值問題，再結合不等式的性質即可求解.

解法6（三角換元法）： 設x2+y2=r2，則有x=rcosα，y=rsinα，

由于x2+2xy-1=0，則有x2+2xy=1，

思維角度7：根據x2+2xy-1=0，引入參數t與0的乘積作差，轉化為二次函數，通過配方，并根據使得不等式成立時對應的系數比較建立參數t的根式方程，通過求解根式方程來確定相應的最值問題即可.

解法7（比較系數法）：由于x2+2xy-1=0，所以x2+y2=x2+y2-（tx2+2xy-1）=（1-t）x2-2txy+y2+t=（x-y）2+t≥t，要使得以上不等式成立，只要2t=2，解得t=不滿足根式方程，舍去），所以

思維角度8：結合極坐標的幾何意義知x2+y2=ρ2表示的是曲線x2+2xy-1=0上的點到坐標原點的距離的平方，進而結合極坐標公式代入關系式1=x2+2xy，通過三角恒等變換，并利用三角函數的圖像與性質來確定相應的最值問題，再結合不等式的性質即可求解.

解法8（極坐標法）：根據極坐標方程可知x2+y2=ρ2，其表示的是曲線x2+2xy-1=0上的點到坐標原點的距離的平方，

而 x=ρcosθ，y=ρsinθ， 所 以 1=x2+2xy=ρ2cos2θ+

思維角度9：結合x2+2xy-1=0得到曲線結合x2+y2=r2表示的是曲線的距離的平方，通過求導，并結合圓的切線方程，建立對應切線的斜率相等，進而得到切點（x0，y0）所對應的值，從而可知x2+y2=r2≥x02+y02來確定相應的最值問題即可.

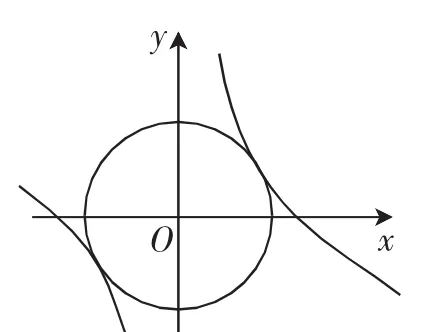
圖1

解法9（數形結合法）：由x2+y2=r2，其表示的是曲線上的點到坐標原點的距離的平方，結合圖1可知當曲線x2+y2取得最小值，此時切點為（x0，y0）（不失一般性，取切點位于第一象限內），由過切點（x0，y0）的切線的斜率為y2=r2上，過切點（x0，y0）的切線方程為x0x+y0y=r2，此時

總結：解決此類兩變元的二次代數式問題，往往根據條件對已知等式進行轉化或處理，將所要求解的雙變元的二次代數式利用換元思維、基本不等式思維、方程思維、三角函數思維以及其他相關的思維方式加以轉化，再結合相關的知識加以解決.

著名數學家、教育學家G·波利亞在《怎樣解題》一書中指出：“好題目和某種蘑菇有點相似之處：它們都是成串成長，找到一個以后，我們應該看看，很有可能在很近的地方又能找到更多的.”通過典型實例的一題多解，可以使得我們的解題思路更加開闊，數學知識的掌握更加熟練，同時思維拓展，妙法頓生，提高解題速度，培養發散思維能力，有助于激發我們學習的主動性、積極性和趣味性，從而全面提高我們的知識水平和思維能力.J