數(shù)學(xué)方法在高中物理電磁學(xué)中的應(yīng)用

崔沐晴

在高中理科科目學(xué)習(xí)的過程中，會用到很多的數(shù)學(xué)方法，其中物理與數(shù)學(xué)的聯(lián)系最為緊密。而高中物理電磁學(xué)這一塊內(nèi)容在高考理綜考試中占有很大比重，高考電磁學(xué)試題中也會涉及很多需要數(shù)學(xué)方法才能夠解決的題目，如果可以靈活熟練地掌握這些數(shù)學(xué)方法，那么解決起這一類題目來就簡單許多。本文主要介紹了在高中物理電磁學(xué)中所運用的幾何法、函數(shù)法和不等式法等。通過了解這一些數(shù)學(xué)方法，學(xué)生可以更容易地去解決問題。

高中的物理學(xué)習(xí)與初中的物理學(xué)習(xí)相比是螺旋式上升的，初中的物理學(xué)習(xí)更偏重于定性知識學(xué)習(xí)，主要了解一些物理學(xué)上最基礎(chǔ)的知識，而高中的物理更加地注重定量計算，其知識深度，理解加深；知識的廣度和范圍增大；對知識的應(yīng)用要求提升。即高中物理學(xué)習(xí)不再僅學(xué)習(xí)基礎(chǔ)知識，更加注重提升學(xué)習(xí)并且利用物理知識解決問題的能力，并且學(xué)會運用一些經(jīng)常使用到的數(shù)學(xué)方法，

一、幾何法在電磁學(xué)中的應(yīng)用

幾何知識在高中物理中的應(yīng)用范圍是比較狹窄的，但是如果有些物理問題能夠巧妙地運用幾何知識，那么這個問題解決起來就非常的容易了。學(xué)生在解決實際問題時不能單純地從靜態(tài)角度思考問題，而應(yīng)該綜合考慮位置及各個狀態(tài)。。如以下這個例子就巧妙地運用了集合中圓的知識來解決電磁學(xué)問題。

例1：圓形勻強磁場的半徑R為10厘米，圓形勻強磁場的邊界與v軸相切于坐標(biāo)原點0點，磁場的磁感應(yīng)強度為0.332T，記為B，放射源S位于坐標(biāo)原點0處，放射源S可以向紙面四面八方發(fā)射速率v=32*10^{6<＼sup>m/s的α粒子，已知α粒子的電量q=32*10-19<＼sup>c，質(zhì)量m=6.64*10-27<＼sup>Kg，那么α粒子通過磁場的最大偏向角是多少？}

解：α粒子在磁場中作半徑為r的勻速圓周運動，可得：

r=mv/Qb=（6.64*10^{-27<＼sup>*3.2*106<＼sup>）/（3.2*10-19<＼sup>*0.332）m=20cm}

從而可以建立一系列半徑為20cm并交于o點的等圓系，

由等圓系很容易得出要使得α的偏向角最大，那么α粒子在磁場區(qū)域內(nèi)的弦最長。

因此α粒子的最大偏向角α=2arcsin（R/r）=60。

二、函數(shù)法在電磁學(xué)中的應(yīng)用

與幾何方法相比，函數(shù)法在電磁學(xué)中的應(yīng)用非常廣泛，在很多情況下都會用到函數(shù)法來解決實際問題。常用的函數(shù)方法有一次函數(shù)法和二次函數(shù)法，以此來找到兩個或者三個變量之間的相互關(guān)系。

1、一次函數(shù)的應(yīng)用

一次函數(shù)是形如y=kx+b（k為不是0的數(shù)）的式子，它反映了因變量v隨著自變量x變化而變化。x與v之間的關(guān)系為線性關(guān)系，例如：靜電場中的Q與U之間的關(guān)系，U和d之間的關(guān)系等。

例2：近些年來，酒后駕車幾乎成了“公害”。警察用于檢測醉酒駕駛的酒精測試儀的工作原理如右上圖，P為半導(dǎo)體酒精氣體傳感器，RO是固定值電阻器，酒精氣體傳感器的電阻為r，其中1/r與酒精氣體的濃度C成正比，。以下四圖是關(guān)于當(dāng)前電流表A的讀數(shù)I與酒精氣體濃度C之間的關(guān)系圖像。四幅圖像中正確的是（ ）

分析：根據(jù)閉合電路歐姆定律

I= U/R可知I與R成反比，而電阻r的倒數(shù)與酒精氣體的濃度C成正比

0++==E

r R r E++0'1.∵r=k

C1.∴I 1=E

r R C E k ++01由上分析可知C結(jié)論正確

2、二次函數(shù)的應(yīng)用

形如y=a2+bx+c這樣的式子是一元二次函數(shù)。一元二次函數(shù)常用來解決求最值和極值的問題。在討論滑動變阻器進行分壓的電路中電流A或電壓V示數(shù)變化問題時，可以把電阻Ω，這個動態(tài)變化量轉(zhuǎn)化成二次函數(shù)y=a2+bx+c形式，運用二次函數(shù)的相關(guān)知識進行配方計算，最終求出極值。

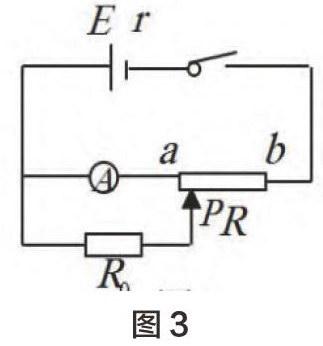
例3：如圖3所示，電源E=6V，內(nèi)阻為r=l歐姆，滑動變阻器R的總阻值為11歐姆，固定電阻R0=3歐姆，求滑動變阻器從a滑動到b過程中，電流表A的讀數(shù)范圍。

解：令A(yù)讀數(shù)I，設(shè)a--p部分電阻為x，則p-b部分電阻為11-x，根據(jù)閉合電路歐姆定律及并聯(lián)電路的電流分配關(guān)系：I=6/（R# +ll-x+r）×3/（x+3）=18/（一（x一6）2+72）可見當(dāng)x=0時，Imax=0.5A，x=6歐姆時，Imax=0.25A，故A示數(shù)范圍為從0.25A到0.5A連續(xù)變化。

三、不等式法在電磁學(xué)中的應(yīng)用

不等式法在數(shù)學(xué)中有廣泛的用途，不等式法對于解決一些范圍問題及最大最小值問題具有十分重要的意義。在高中物理電磁學(xué)中的一些不定量的求解也用到了不等式的相關(guān)知識。比如在串并聯(lián)電路中改變某些因素，其中電流、電壓、電阻的改變等量同種電荷、場強的變化和大小、材料帶電量都一樣的同種電荷接觸后在還原過程中電荷的變化。

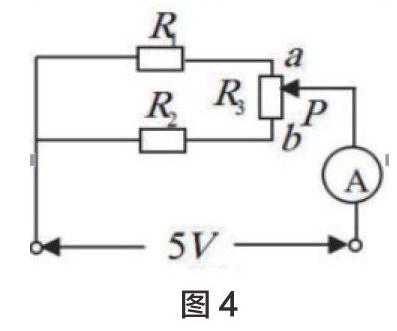
例4：如圖4所示，已知Rl是2歐姆，R2是3歐姆，其中滑動變阻器的最大值R3是5歐姆，當(dāng)滑動變阻器的滑片P從a滑到b的過程中時，電流表A能夠達到的最小值是？

解：由歐姆定律知，要求得電流表A最小值，那么，外電路的電阻就應(yīng)該保持最大值。

設(shè)a-p部分的電阻為x，則b-p部分的電阻5-x

1/R=1/（2+x）+1/（3+（5一x））

化簡可得R =（2+x）（8-x）10

令a=2+x，b=8-x， 又a+b=10， 因此當(dāng)且僅當(dāng)a=b時，即2+x=8-x

亦即x=3時ab：，故有（2+x）（8一x）：（）=25，所以電流表最小是2A。

在高中物理電磁學(xué)解題過程中，要靈活地運用這幾類方法，有時候甚至可能會用到這幾種方法中的兩種或者兩種以上，這樣在解決問題時，一方面要運用物理知識，另一方面又要結(jié)合一定數(shù)學(xué)方法，盡量做到運用準(zhǔn)確的數(shù)學(xué)語言和公式來表示答案，以求進一步提升學(xué)生學(xué)習(xí)物理和解決物理問題的知識。