運用平方差公式進行計算過程中存在的問題及應對策略

金培苗

（灌云縣九年制實驗學校，江蘇 灌云）

平方差公式是蘇科版七年級數學下冊第9章第4節第二課時所學習的內容，學生對于平方差公式都能說上來：（a+b）（a-b）=a2-b2，但是在運用過程中，總會出現各式各樣的錯誤。下面我就針對存在的問題和大家談談應對策略。

一、練習中的錯誤舉例

錯誤類型 1：（x+3）（x-3）=（x-3）2（x-3）（x-3）=x2-32

錯誤原因剖析：平方差公式的結構特點沒有掌握，與完全平方公式的特點弄混了。

錯誤類型 2：（-2+x）（2+x）=（-2）2-x2=4-x2（-3+x）（x+3）=（-3）2-x2

錯誤原因剖析：沒有掌握好平方差公式的特點，后面的結果前后兩部分弄顛倒了。

錯誤類型 3：（2x-3y）（2x+3y）=2x2-3y2

錯誤原因剖析：沒有掌握好平方差公式的特點，套用公式時丟掉了括號。

錯誤類型 4：（2a-3b+c）（2a+3b+c）=（2a-3b）2-c2=4a2-12ab+9b2-c2

錯誤原因剖析：沒有掌握好平方差公式的特點，沒有弄清哪些是相等的量、哪些是互為相反數的量。

二、應對策略

1.弄清公式特點和條件

平方差公式左邊前后括號里的多項式的項數相同，其中在前后括號里有一部分項是相等的，另外一部分則是互為相反數的。公式右邊有兩部分，前部分是相等量的平方，后部分是互為相反數的量的項的平方，中間用“—”號連接。如下圖：

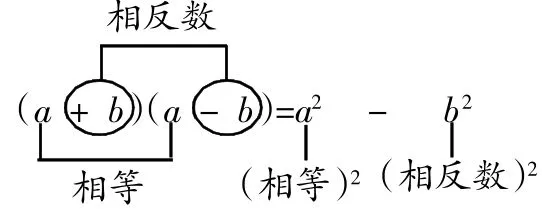
使用平方差公式進行計算必須滿足如下幾個條件：

（1）前后括號內的項數要相同；

（2）前后括號內要有相等的項，前面括號內余下的項和后面括號余下的項是互為相反數關系。

2.教會學生套用公式

在解題的時候一定要認真審題，找到前后括號內相等的項和互為相反數的項，然后根據上面的公式進行計算。

例 1 計算：（1）（2a-3b）（2a+3b） （2）（3x-y）（-y-3x）

解析：在（1）中第一個括號內2a和第二個括號內的2a是相等的項，第一個括號內-3b和第二個括號內3b是互為相反數的項，所以根據公式可得：（2a）2-（3b）2，然后再依據積的乘方公式進行計算即可。在（2）中第一個括號內-y和第二個括號內的-y是相等的項，第一個括號內3x和第二個括號內-3x是互為相反數的項，所以根據公式可得：（-y）2-（3x）2，然后再依據積的乘方公式進行計算即可。

解題過程如下：

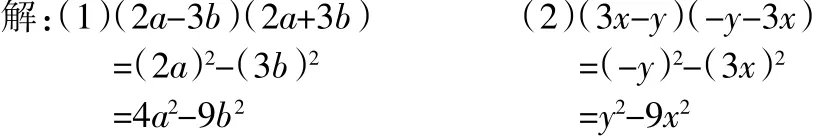
對于復雜的題目也是一樣的操作方式，例如：

例 2 計算：（1）（2a+3b+c）（2a+3b-c）

（2）（3x-y-4z）（4z-y+3x）

解析：在（1）中第一個括號內2a，+3b和第二個括號內的2a，+3b是相等的項，第一個括號內+c和第二個括號內-c是互為相反數的項，所以根據公式可得：（2a+3b）2-（c）2，然后再依據相關公式進行計算即可。在（2）中第一個括號內3x，-y和第二個括號內的3x，-y是相等的項，第一個括號內-4z和第一個括號內4z是互為相反數的項，所以根據公式可得：（3x-y）2-（4z）2，然后再依據相關公式進行計算即可。

解題過程如下：

（1）（2a+3b+c）（2a+3b-c）

解：原式=（2a+3b）2-（c）2

=（2a）2+2·2a·3b+（3b）2-c2

=4a2+12ab+9b2-c2

（2）（3x-y-4z）（4z-y+3x）

解：原式=（3x-y）2-（4z）2

=（3x）2-2·3x·y+（y）2-16z2

=9x2-6xy+y2-16z2

注意：在套用公式的過程中要注意，我們找到相等的項，將它們連同它們的符號直接填入前面的括號里然后把它們的和加平方；至于互為相反數的項，我們只選擇前一個括號余下的項，要連同本身的符號直接填入后面的括號里，然后加平方（也可以選擇后面括號里除去與前面括號里相等的項余下的項，也要連同其符號一起填入后面的括號里，然后加平方）。

例 3 計算（2a-3b+5c-4d）(4d-3b-5c+2a）

解析：此題前后括號內的項數都是4，而且前后括號內有相等的項，然后前后括號內剩下的項是互為相反數，可以套用平方差公式計算。在第一個括號內2a，-3b和第二個括號內的2a，-3b是相等的項，第一個括號內+5c，-4d和第二個括號內-5c，4d是互為相反數的項，所以根據公式可得：（2a-3b）2-（5c-4d）2，然后再依據相關公式進行計算即可。解題過程如下：

解：（2a-3b+5c-4d）（4d-3b-5c+2a）

=（2a-3b）2-（5c-4d）2

=（4a2-12ab+9b2）-（25c2-40cd+16d2）

=4a2-12ab+9b2-25c2+40cd-16d2

從上述幾個例子可以看出，運用平方差公式進行計算，可以使計算過程變得簡便。但要強調的是，用平方差公式進行計算，前提是所給的題目的特點要符合平方差公式的特點和條件，如果不符合，則不可亂用，否則會弄巧成拙。因此，只有弄清公式的結構特點，然后再套用上面所給定的公式完成計算，才能達到簡便、準確、高效、快捷的效果。