關于一道高考題的思考

陳飛龍

（合肥市第七中學，安徽 合肥）

首先我們來看看原題和給出的參考答案：

25.（20分）如圖，兩水平面（虛線）之間的距離為H，其間的區域存在方向水平向右的勻強電場。自該區域上方的A點將質量為m、電荷量分別為q和-q（q＞0）的帶電小球M、N先后以相同的初速度沿平行于電場的方向射出。小球在重力作用下進入電場區域，并從該區域的下邊界離開。已知N離開電場時的速度方向豎直向下；M在電場中做直線運動，剛離開電場時的動能為N剛離開電場時動能的1.5倍。不計空氣阻力，重力加速度大小為g。求

（1）M與N在電場中沿水平方向的位移之比；

（2）A點距電場上邊界的高度；

（3）該電場的電場強度大小。

看到這一題參考答案的解法（此處略去），很多學生感到思維連貫性不強，也就是感到物理過程理解不透徹，即是說看著答案我能把每步驟看懂，但是自己去解題的過程中可能不知道要這么入手，筆者在求解本題的過程中使用的方法與參考答案有些區別，現供讀者參考。

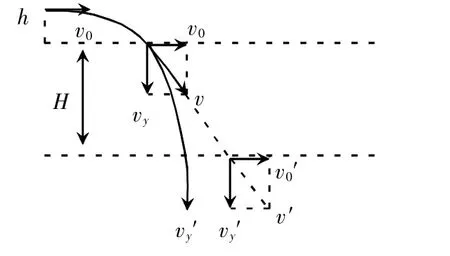
方法一：

（1）進入電場后，M、N水平方向做勻加速，豎直方向也做勻加速直線運動，水平和豎直具有等時性：

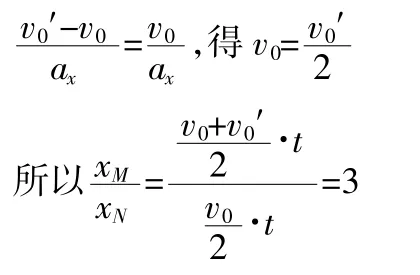
（2）由上問知 v0′=2v0，vy′=2vy，v′=2v

利用豎直方向勻加速得：

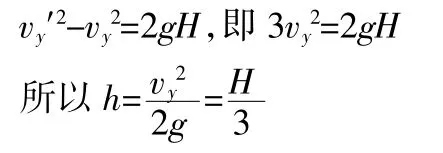
這種方法的優點在于先指出M剛進入電場和剛離開電場之間速度的2倍比例關系，由此來進行計算和分析較直觀和方便。

方法二：

對于本題的求解，我們也可使用動量定理：

（1）對M、N的水平方向分別應用動量定理得

-Eq·Δt=0-mv0

Eq·Δt=mv0′-mv0

于是得：v0=v0′-v0，即 v0′=2v0

由此知 vy′=2vy，v′=2v

（2）對M的水平和豎直方向分別應用動量定理得：（Δt為在電場中的時間）

Eq·Δt=m（v0′-v0）

mg·Δt=m（vy′-vy）

兩式相比可得：

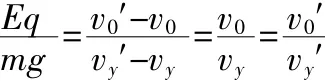
（3）由 Eq·Δt=m（vy′-vy），vy′=2vy，得 vy=g·Δt，于是知道平拋運動的時間與在電場中的時間相同。

再由豎直方向自由落體的規律知：

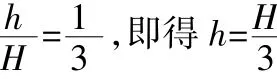
本題的幾種求解方法各有不同之處，參考答案上側重于直接使用運動學公式和動能定理，直來直去，需要對題目有較深的理解和運算能力，筆者給出的兩種解法主要把握住水平和豎直兩方向的分別分析，強調兩方向的運動等時性，并注意M出電場和入電場時合速度和各分速度的比值關系，從而可適當降低運算量以利于學生理解。