高中數(shù)學(xué)中如何由遞推關(guān)系求數(shù)列的通項(xiàng)
董根娥
(山西省大同市南郊教師進(jìn)修學(xué)校,山西 大同)
類型一:累加法(型如:an+1=an+f(n))

以上n-1個(gè)式子相加得:an-a1=lnn,
又a1=2,∴an=2+lnn.
類型二:累乘法(型如:an+1=g(n)an)
【解析】原式可化為[(n+1)an+1-nan](an+1+an)=0.
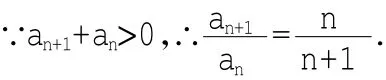
以上n-1個(gè)式子相乘,得
類型三:構(gòu)造新數(shù)列法(型如:an+1=can+d)(c≠1 且d≠0)
例 3.已知數(shù)列{an}中,a1=1,an+1=2an+3,求an.
【解析】(an+1+λ)=2(an+λ),可得 λ=3
∴(an+1+3)=2(an+3)
∴數(shù)列{an+3}是公比為2,首項(xiàng)為a1+3=4的等比數(shù)列.
∴an+3=4·2n-1=2n+1
∴an=2n+1-3.
類型四:(型如an+1=c·an+f(n))
例 4.在數(shù)列{an}中,a1=-1,an+1=2an+4·3n-1,求通項(xiàng)an.
類型五:取倒數(shù)法
例 5.已知數(shù)列{an}中,a1=1,且當(dāng)n≥2 時(shí),,求數(shù)列{an}的通項(xiàng)公式.
類型六:取對(duì)數(shù)法
例 6.若數(shù)列{an}中,a1=3,且,求通項(xiàng)an.
【解析】由題意:an>0,將兩邊取對(duì)數(shù):lgan+1=2lgan
∴數(shù)列{lgan}是公比為2,首項(xiàng)為lga1=lg3的等比數(shù)列.
∴l(xiāng)gan=2n-1·lg3
∴an=32n-1.
類型七
例 7.已知數(shù)列{an}滿足a1+2a2+3a3+…+nan=n(n+1)(n+2),求通項(xiàng)an.
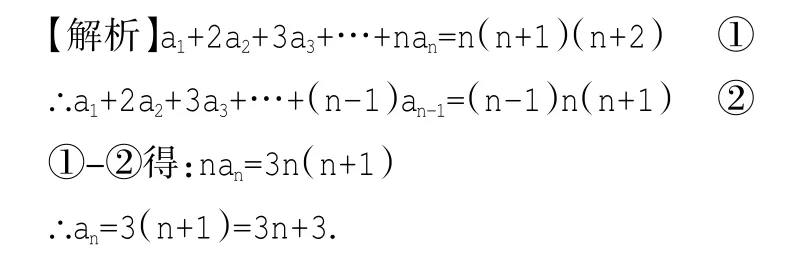
【解析】(an+2)2=8Sn①
(an-1+2)2=8Sn-1②(n≥2)
①-②得:(an+2)2-(an-1+2)2=8an,化簡(jiǎn)得:(a1+an-1)(an-an-1-4)=0.
∵an>0 ∴an+an-1>0 ∴an-an-1=4 ∴ 數(shù)列{an}是公差為4的等差數(shù)列.
又∵a1=S1=2 ∴an=4n-2
以上的類型是高中數(shù)列中已知遞推關(guān)系求通項(xiàng)的常用類型,請(qǐng)同學(xué)們細(xì)心領(lǐng)會(huì),認(rèn)真掌握.

