促銷策略角度下允許缺貨的兩層庫存模型規劃

陳香堂 ，馬衛民，孫秉珍

（1.同濟大學 經濟與管理學院，上海 200092；2.溫州職業技術學院 工商管理系，浙江 溫州 325035；3.西安電子科技大學 經濟與管理學院，西安 710071）

隨著商品經濟與網絡經濟的快速發展，及時適應消費者的需求以及迅速做出市場反應已經成為市場競爭的有力武器。保持適量庫存以獲取競爭優勢是經常采取的一種策略，因此，庫存系統的管理已經成為非常重要的管理問題。零售商經常要解決訂貨時間和訂貨批量這兩個基本問題。為了達到收益值最大化的目的，一般要綜合考慮產品的制造成本、庫存成本和訂貨成本等因素。此類問題的經典解決思路是運用Harris的經典經濟批量模型（EOQ）。經典EOQ 模型的基本假設是不允許缺貨、庫存能夠得到及時補充的情況。經典EOQ 模型認為缺貨將導致產品脫銷而喪失了銷售機會，Zipkin[1]討論了缺貨情況，并將其推廣至經濟生產批量模型（EPQ）。隨后，不同學者深入研究了缺貨情況，并認為現實中有些顧客愿意繼續等待，有些則不會。對于是否含有缺貨變量的模型最早出現在Fabrycky等[2]以及Ali[3]的研究中。Montgomery等[4]給出了此類問題的解決方法。現實商業運作中經常出現缺貨狀態，而不允許缺貨的假設在一定程度上限制了EOQ 模型的應用范圍。因此，很多學者從多個角度系統研究了允許缺貨的庫存問題。Deb等[5]是其中具有代表性的研究之一，其從允許缺貨的角度拓展了已有模型。其他學者在該拓展模型基礎上進行了一系列深入研究[6]。

眾所周知，在現實的商業操作中，由于市場位置的租賃成本較高，故零售商會在店面內開發出一個儲存少量產品的小倉庫。為了配合促銷策略產生的大量銷售或在市場需求量較大時，零售商訂貨量超過小倉庫的容量也許能獲得更大的收益。考慮到銷售的便利性、降低產品成本以及降低銷售機會成本等目的，一些銷售商采取同時擁有店面庫存倉庫和租賃庫存倉庫兩個庫存倉庫的策略。

然而，在某些具體的現實情境和具體的操作實踐中，另外租賃倉庫對于零售商并不一定是盈利的，特別是租賃倉庫成本很高時。此時必須考慮如下問題：零售商堅持一個店面倉庫還是再租賃第2個倉庫。一些學者分別從無限補貨率和有限補貨率的角度研究了雙層庫存模型；而另一些學者則從市場需求角度提出了雙層庫存模型。Hartley[7]研究了兩層倉庫模型。Zhou等[8]考慮運輸成本，建立了存貨和市場需求相互獨立的雙倉庫庫存模型。在充分考慮現實問題具體特征的基礎上，針對雙層倉庫庫存模型[9-11]的研究是近年來較為有代表性的研究。

在市場競爭日益加劇的情形下，促銷措施已經成為商業運作的重要策略。一方面，促銷措施有助于新產品的推出、延長產品的生命周期、擴大產品的市場占有率。促銷措施一般包括免費禮物、折扣優惠、配送便利、更好的服務和廣告等措施。另一方面，促銷措施的實施必然會引起市場需求的變化，從而影響庫存的管理策略。Goyal等[12]研究了不同促銷措施影響產品市場需求的多階段生產體系中的經濟訂貨批量，并給出了整合的生產-庫存-市場模型。Nair等[13]研究了免費禮物、價格折扣和特殊服務等方式形成的促銷效果對庫存的影響，并對此進行了優化設計。Krishnan等[14]的研究結論證明了價格優惠、產品展示、免費物品和廣告是獲得最大收益的基本策略。Sun[15]研究發現，顧客和不同促銷類型存在一定關系，特別是促銷措施強化了品牌對顧客行為的影響。另一些學者從數量折扣、價格折扣以及延期支付等角度研究了庫存管理的優化策略[16-18]。Sana等[19-24]從影響需求的企業動機、銷售人員動機和允許缺貨等角度研究了EOQ 模型。

盡管對于兩層庫存規劃問題的研究獲得了較多成熟且系統的研究模型和方法，并獲得了諸多有價值的研究結論；但是關于兩層庫存規劃的研究和對于考慮促銷策略影響市場需求變化情況[24]的研究尚不多見；同時，目前針對允許缺貨的促銷策略情景下的庫存規劃的研究中亦很少有結合兩層庫存的相關研究[11]。現實中，允許缺貨、促銷策略的實施和兩層庫存已經成為現實商業運作中的常態[11]，為了更好地解決現實中出現的問題，本文考慮在允許缺貨的約束下，從促銷策略影響市場需求的角度研究兩層倉庫庫存系統，討論如何確定促銷措施的力度以及最優的缺貨量，進而制定訂貨批量最優策略，最終實現庫存系統收益的最大化。

1 數學模型的構建

考慮到市場需求受促銷策略的影響以及雙層庫存系統與單層庫存系統之間的差異，本文從促銷策略影響市場需求、雙層庫存之間聯系以及決策變量等方面進行一些合理的模型假設，詳細說明模型所需的符號及參數，并在此基礎上建構目標函數。

1.1 模型假設

為便于模型的建立，作如下假設：

（1）生產商產能有限，允許缺貨。最優訂貨量和允許缺貨量同時決策。

（2）零售商有兩個庫存倉庫，分別為店面庫存倉庫OW（Own Warehouse）和租賃庫存倉庫RW（Rented Warehouse），店面庫存倉庫位于店面內部，租賃庫存倉庫位于離店面不遠處。管理人員經常檢查庫存情況，保證店面庫存倉庫OW 的庫存水平充足。若倉庫OW 貨源不足，將及時、持續地從RW補貨。OW 的庫存下降到某一水平庫存時，發出補貨指令，且補貨及時。貨物到達后，先解決缺貨問題，再補充OW 庫存至充足水平，余下貨物最后運往RW 保存。OW 至RW 之間的運輸成本忽略不計。

（3）促銷策略將在很大程度上促進商品的市場需求，市場需求率是關于促銷因子的函數，即D=x⊕d（ρ）[24]，一般常數x＞0。⊕表示“+”或“×”的運算符號，這將根據商品的特點、市場競爭情況與促銷策略之間的關系而定。此外，假設ρ為促銷因子，反映了促銷策略所產生的市場需求效果，該因子可促進商品的市場需求增加。而，其中τ為常數，一般地，τ＞0。

（4）店面主要用于商品的正常經營，在保證店面正常經營所需的必要場所外，利用剩余不多的店面空間開發店面倉庫（OW）。OW 的庫存不超過OW 的庫存容量，庫存不影響店面的正常經營，可認為在固有經營模式下店面大部分成本主要用于支付店面經營的租金，屬于商品的經營成本。此時，OW 的庫存容量為有限，且不影響店面的正常經營[11]。

1.2 符號說明及參數

本文建模設計參數：

D——每年市場需求率

q——每周期訂貨量

s——每周期缺貨數量

c2——RW 的單位庫存成本

c22——OW 的單位庫存成本

c1——每次訂貨成本

p1——單位產品的購買成本

s1——單位產品銷售價格

c3——單位缺貨成本

k——促銷成本的比例參數

kρm——促銷成本

w——OW 的庫存容量

m——促銷成本的彈性參數，m∈Z+

Z——本文的收益函數

T——周期時間

Z24——文獻[24]的收益函數

1.3 目標函數的建立

在時間0到時間t1，庫存量由（q-s）減少至w，此時RW 庫存為0。再經過時間t2，庫存量為0，此時OW 庫存為0。t3為缺貨時期。周期時間T=t1+t2+t3。上述庫存變化情況如圖1所示。

圖1 OW-RW 庫存變化圖

考慮到收益與銷售收入、訂貨成本、庫存成本、缺貨成本和促銷成本有關，因此，收益函數模型為

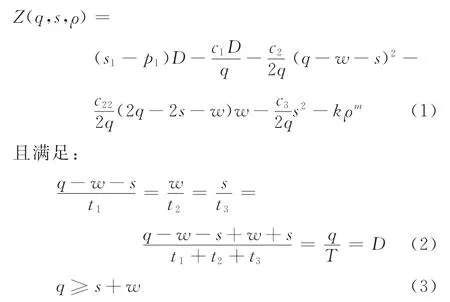
根據上述假設和分析可知，由于每周期訂貨量和每周期的缺貨數量與市場需求率相關，市場需求率是關于促銷因子的函數，故每次訂貨量和缺貨量也可認為是關于促銷因子的函數，進而認為收益函數是關于促銷因子的函數。其中，促銷因子為決策變量，而每次訂貨量和缺貨量為中間變量。由此可知，優化的目標函數就是最大化收益函數Z[q（ρ），s（ρ），ρ]。其中，

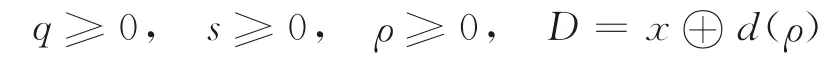
且滿足式（2）、（3）。

2 模型求解

定理1對于任意ρ∈R+，存在唯一的q*和s*，收益函數Z達到最大值。此時，

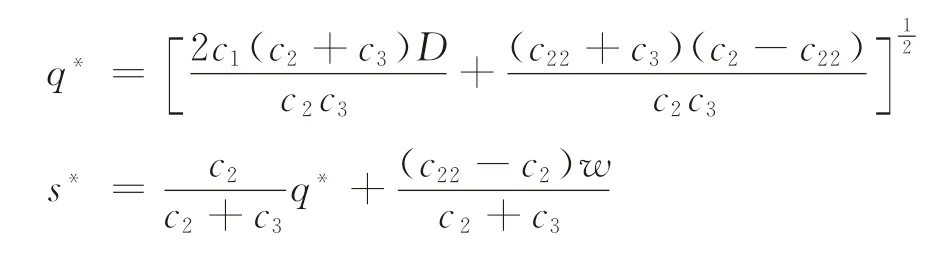
其中，q≥0，s≥0，D=x⊕d（ρ），ρ≥0且滿足式（2）、（3）。

證明顯然，收益函數Z是關于促銷因子的函數，在定義域內且為連續可積可微函數。根據定理條件，不妨假設：

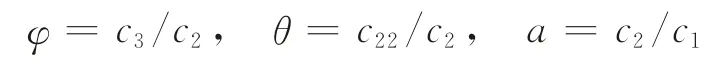
且?＞0，θ＞0，a＞0。將上述假設代入式（1），得

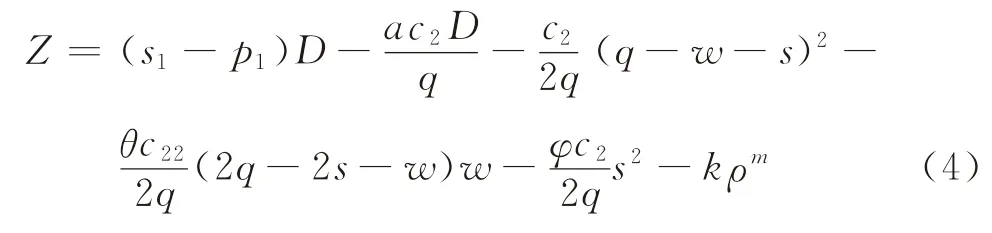
對式（4）分別求偏導，得：

根據假設可知，c22＜c2，即0＜θ＜1，可得：

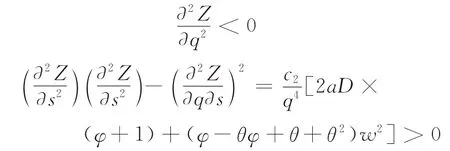
由上述分析可知，收益函數Z[q（ρ），s（ρ），ρ]是關于決策變量促銷因子的函數，每次訂貨量和缺貨量為中間變量，且存在最大值。可令?Z/?q=0，?Z/?s=0，整理得：

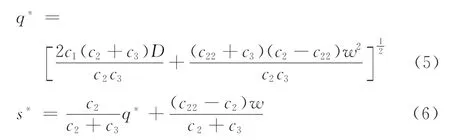
綜上所述，對于任意ρ∈R+，存在唯一的q*和s*，使得收益函數Z達到最大值。 證畢

將q*和s*代入收益函數Z，整理可得

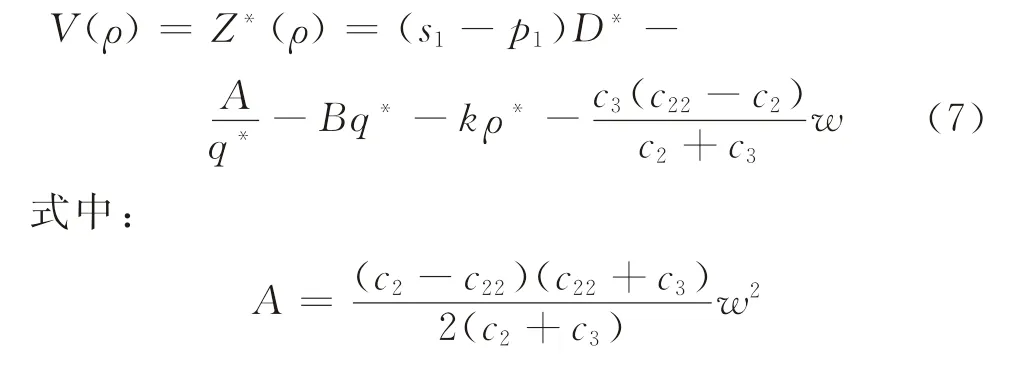
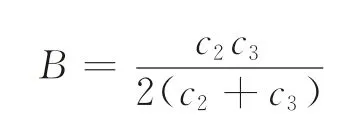
綜上所述，求解V（ρ）最大化，存在ρ的最優解ρ∈R+，只需當時，求解出ρ*，并保證。通過觀察V（ρ）可知，當ρ→∞時，V（ρ）→-∞。這表明，ρ存在上限解，使得V（ρ）＞0。不妨假設V（ρ）=0時，ρ的上限解為ρ**。

3 對比研究

考慮到文獻[24]中主要研究了促銷策略角度下的單庫存系統的收益問題，為此，本節將通過與文獻[24]中的數學對比分析，列出兩種不同類型的數學模型，并盡量采用與文獻[24]中相同的數值進行驗算，研究促銷因子影響程度和參數靈敏度，期望從與文獻[24]的對比研究中得到有意義的研究結論。

3.1 數學對比分析

通過對比文獻[24]，本文的收益函數為

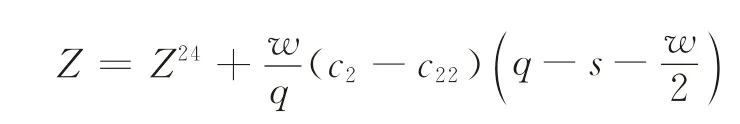
由假設可知，當w=0，或c22=c2時，即當OW 庫存容量為0，或者單位OW 庫存成本和單位RW 庫存成本相等時，兩層庫存模型將轉變為單庫存模型。因此，本文的模型拓展了文獻[24]中的模型。

一般的，Z≥Z24，即相同成本結構條件下，雙層庫存收益值不小于單層庫存的收益值。這主要的原因是在保持正常經營的店面內開發了成本較小的店面倉庫。增加的收益主要取決于OW 單位庫存成本和RW 單位庫存成本之間的差值，以及OW 的庫存容量w。由函數分析可知，w在定義域[0，q-s]內與收益值之間呈正相關的趨勢。因此，店面倉庫庫存不影響正常經營以及充分利用店面倉庫容量必須同時兼顧，缺一不可。

3.2 數學模型

市場需求D與促銷因子ρ之間存在兩種對應的關系[24]，所需優化的目標函數分為模型I和模型II兩種模型，即

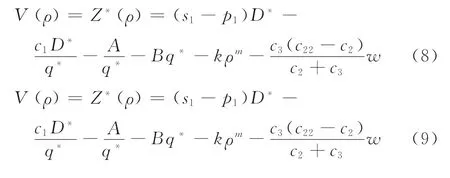
式中，D*=x+τρ/（1+ρ），且滿足式（2）、（3）以及式（5）、（6）。

3.3 數值驗算

針對模型I和模型II，為了便于對比研究，不妨參照文獻[24]取值：x=70，τ=20，c1=28，c2=20，c22=10，c3=100，m=3，s1=20，p1=12，k=18，w=10，則：

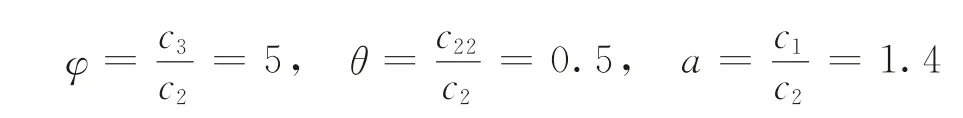
運算結果如表1、2所示。

表1 模型I和模型II的優化結果

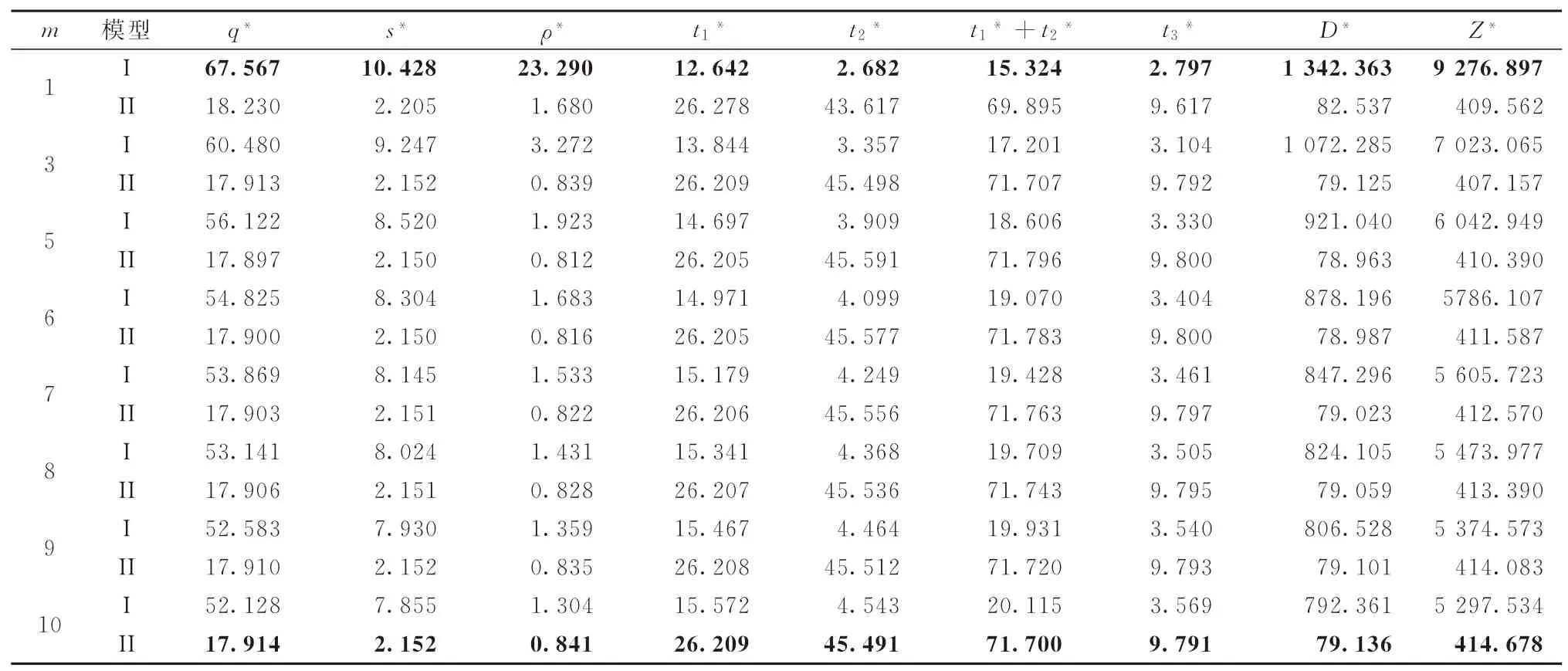
表2 不同m 值的模型I和模型II的優化結果

由表1、2以及對照文獻[24]中的表1、2可知，由于店面倉庫的存在，收益值均比相應無店面倉庫的情況增加。與文獻[24]中不同的是，庫存存儲時間是隨著m而發生變化的，盡管變化的范圍并不大。

通過運算可知，模型I、II的收益值和m值的相關性呈現不盡相同的趨勢。m值是根據歷史數據得到的經驗估計值，一般而言，m值是固定的參數。表2給出了各種m值不同情況下的收益最優的結果。

3.4 促銷因子ρ值的影響分析

根據假設，促銷因子的變化將影響市場需求，從而進一步影響收益值。模型I、II的促銷因子取值范圍分別為（0.25，7.92），（0，2.935），收益值的變化情況如圖2、3所示。由圖2、3可知，模型I、II的促銷因子ρ分別達到3.272和0.893時，收益值最大，分別為7 023.065和407.157。結合圖形和運算結果可知，上述兩種模型分別表示兩類典型產品類型：模型I不做促銷時，市場需求為0，收益值為負數，即-40.27；模型II不做促銷時，市場需求不為0，收益值為正數，即359.412 4。

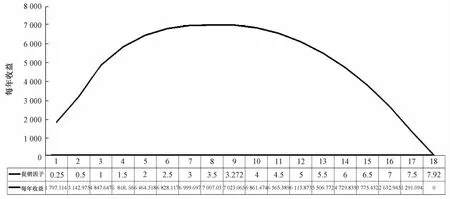
圖2 模型I促銷因子和每年收益函數圖

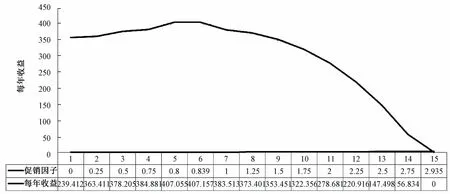
圖3 模型II促銷因子和每年收益的函數圖

這與現實情況比較相符，為確保收益值達到最優，促銷力度（促銷因子）因視產品成本結構等實際情況而確定，不宜過大或過小。對比文獻[24]中的圖2、3，本文的圖2、3相對比較完整地顯示出促銷因子和收益函數之間的關系。

3.4 靈敏度分析

對模型I的參數c1、c21、c22、c3、x、τ、s1、p1和k進行靈敏度分析，各參數獨立采取從-50%～50%數值變化，從而觀察收益值的變化情況；對模型II的參數靈敏度分析分別采用w=0和w=10兩種情況進行比對，各參數獨立采取從-50%～50%數值變化，從而觀察收益值的變化情況。運算結果如表4～6所示。

由表4可以看出，模型I中的參數s1和p1為高靈敏度參數，x和τ為中靈敏度參數，c1、c21、k、c22和c3為低靈敏度參數。當銷售價格s1增至原來的50%時，模型I的收益達到最大值18 070.070。

由表5可以看出，模型II中的參數s1和p1為高靈敏度參數，x和c1為中靈敏度參數，c21、c22、c3、τ、和k為低靈敏度參數。當銷售價格s1增至原來的50%時，模型II的收益達到最大值1 207.525。

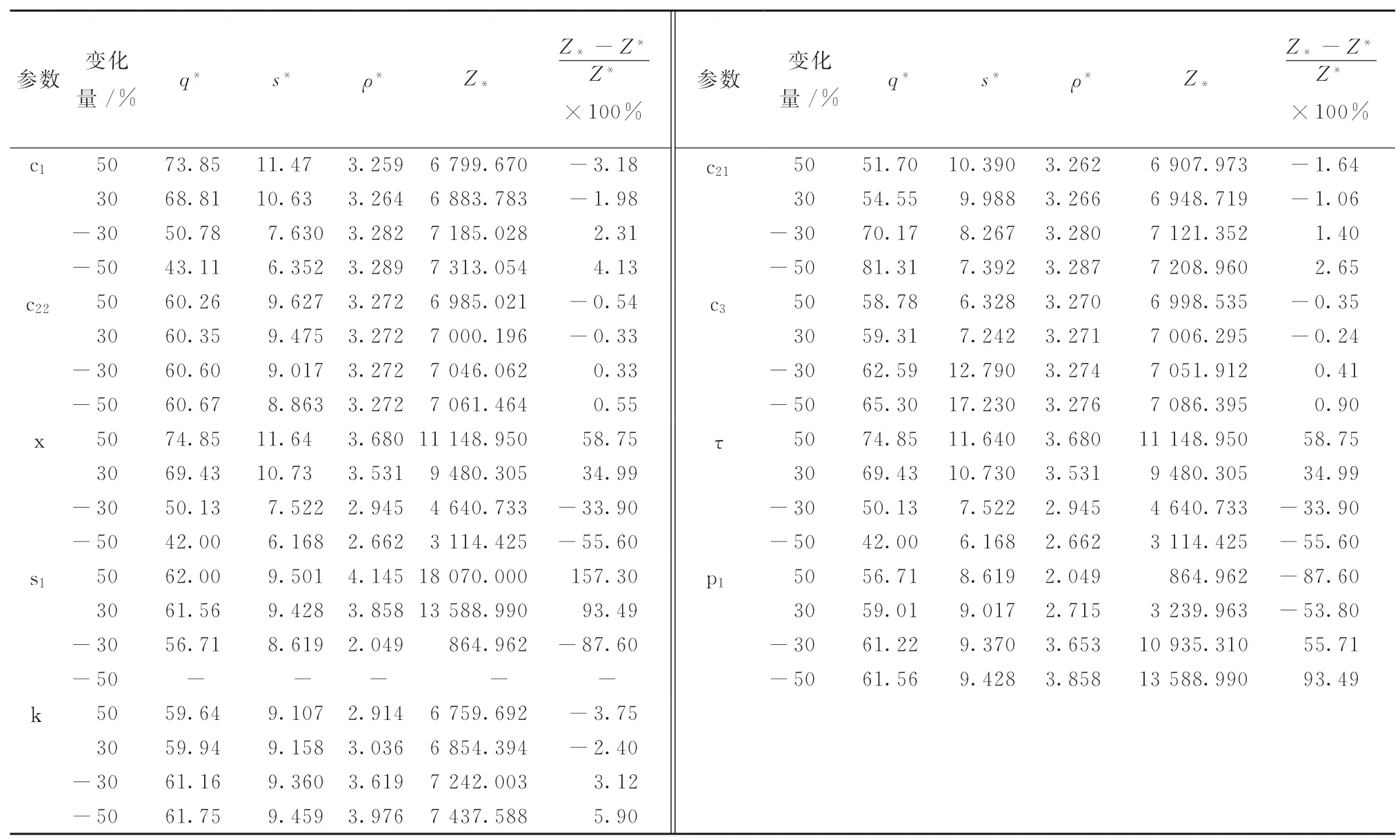
表4 模型I參數靈敏度分析

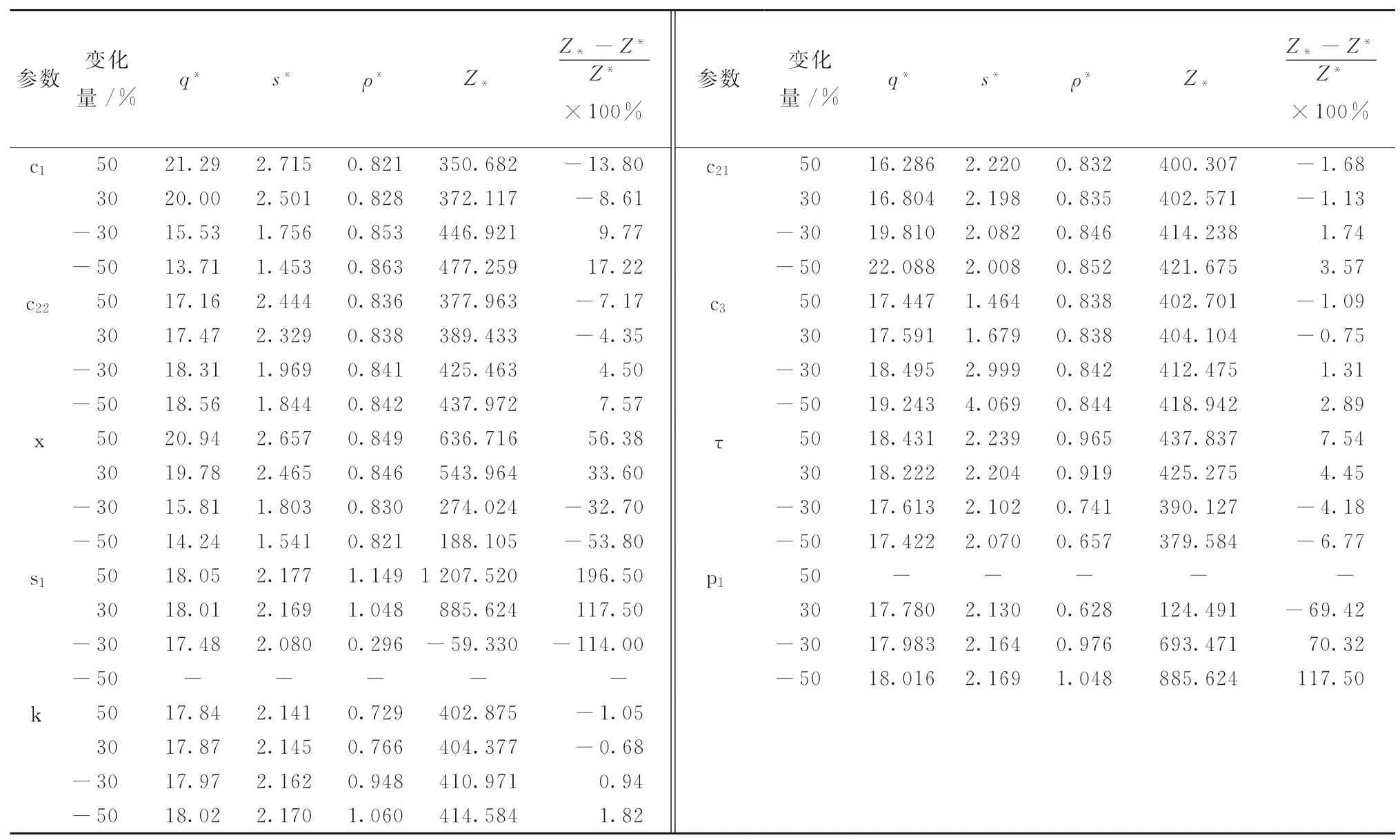
表5 模型II參數靈敏度分析(w=10)

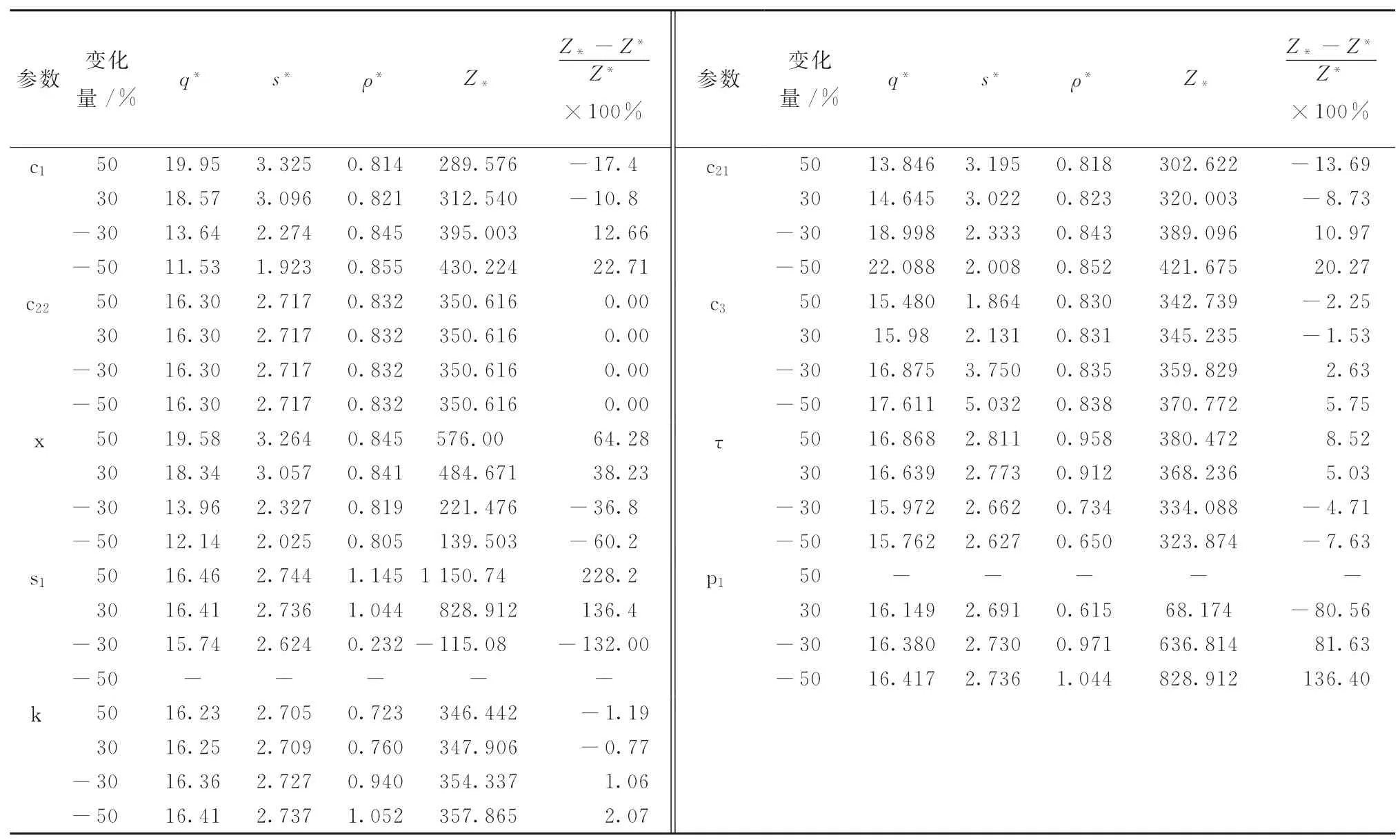
表6 模型II參數靈敏度分析(w=0)

對比文獻[24]中的表7（以下簡稱表7）和本文的表4可以看出，同等條件下，表4的各參數靈敏度均小于表7，而此時的收益值卻均大于表7的收益值。類似地，同等條件下，表5中的各參數敏感度均小于表6，而此時的收益值卻均大于表6 的收益值。因此，可以認為店面倉庫在一定程度上降低了收益值的波動率而提高了同等條件下的收益值。

4 結論

本文從實施促銷策略角度構建了允許缺貨的兩層倉庫庫存模型，假設模型的收益值是關于促銷因子的函數，根據產品類型分為兩種不同形式的模型，并深入研究了店面倉庫庫存容量以及促銷因子等因素對兩層庫存系統收益的影響。通過數值分析，獲得了如下主要結論：

（1）對于不同產品或相同產品處于不同的競爭環境下，促銷策略的實施效果不盡相同。實施促銷策略之前，明晰本產品的收益值函數的組成形式，充分重視收集產品的歷史數據，確定合適的促銷力度等，以達到收益值最大。

（2）對于單層庫存而言，兩層倉庫中的店面倉庫容量改變了單層庫存的成本結構，并起到了減少收益值的波動性和提高收益值的雙重作用。進而，在確保店面庫存容量不影響店面正常經營的前提下，充分利用店面倉庫容量，綜合考慮歷史數據等因素，可通過事先規劃店面倉庫容量的方法，提高收益值的水平；或在店面倉庫容量固定的情況下，通過調整促銷力度等因素，優化收益值。

（3）對于兩類不同形式的產品，提高銷售價格和降低購買成本均可迅速增加收益值。若上述兩種方式均不可行時，符合模型I的產品可通過增加參數x和τ而達到收益值最優，即通過生產真正符合消費者需求的產品以及根據產品類型和消費者特點采取適宜的促銷方式增加促銷效果等方法；符合模型II的產品可增加參數x、減少參數c1，使得收益值最優，即除了生產真正符合消費者需求的產品外，還可通過努力降低每次訂貨成本等方法。

結合模擬算例的比較和靈敏度分析易知，本文所建構的模型進一步拓展了文獻[24]中經典模型的結論及其適用范圍，較為全面地刻畫出兩層庫存的商業運作情況。同時，通過定量理論模型分析系統地闡明了促銷因子等因素與收益值之間的關系，進而給出具有針對性的、可行性較強的對策建議。因此，本文所構建的模型能夠盡可能地刻畫實際中的庫存問題特征，因而具有較好的應用型和適用性。

事實上，在本文研究的基礎上，考慮到競爭環境下促銷因子等因素不應保持不變，如若將促銷因子等參數進行模糊化處理，可進一步提高模型的適用性。另外，本文未考慮零售商最優訂貨量和允許缺貨量的決策次序，也未考慮兩類模型所代表的具體產品類型及其特征。這些問題將在未來的研究工作中繼續深入探討和研究。