基于改進K＿means的發動機狀態評估方法

谷廣宇，劉建敏，喬新勇

前言

發動機作為裝甲車輛的心臟，其技術狀況的優劣直接影響車輛性能和戰斗力，因此如何科學有效地評估發動機技術狀況，已成為部隊關注的重點。目前，我軍在裝甲車輛發動機技術狀況評估方面，已經做了部分研究[1-2]，然而這些研究主要集中在根據先驗樣本數據建立評估模型，對未知樣本進行評估，而對于在沒有先驗知識的情況下，如何確立發動機各技術狀況等級的劃分基準的研究，仍相對缺乏。

現有對發動機狀況等級基準劃分的研究中，文獻[3]中提出了將發動機根據摩托小時劃分技術狀況階段，再擬合各階段的平均值確定相應等級的評估基準。文獻[4]中提出了利用主成份分析法根據散點圖分布劃分技術狀況區域，再通過神經網絡建立評估模型。這兩類方法解決了沒有先驗知識的情況下有效評估發動機技術狀況的問題，但無論是以摩托小時進行階段的劃分，還是以散點圖分布進行區域劃分，都存在很大的主觀因素，不同的劃分標準也會對最終的評估結果造成很大影響。由于環境條件、工作強度等因素影響，發動機的實際技術狀況存在很大隨機性，不同樣本下建立的評估基準與評估模型可能存在較大差異，并且由于受試驗成本、試驗周期等條件的限制，通常無法進行大量試驗來獲取大樣本，這也會增加樣本隨機性對評估模型的影響，難以保證其最終得到評估結果的可靠性。

為解決上述問題，本文中通過改進K＿means聚類算法，利用試驗樣本數據分布，計算各等級聚類中心及其分類，建立更加客觀穩定的評估模型，實現基于數據驅動的發動機狀態評估，并融合Bootstrap小子樣統計方法，利用其通過再生抽樣將小樣本問題轉化成大樣本的特性，削弱試驗樣本隨機性對評估模型的影響，增強發動機評估模型的穩定性。

1 K＿means算法

K＿means算法是一種典型的基于劃分的聚類算法，屬于無監督機器學習方法的一種。該算法將一個含有n個樣本的集合劃分為K個子集合，其中每個子集合代表一個類簇，同一類簇中的樣本具有高度的相似性，不同類簇中的樣本相似度較低。

1.1 K＿means算法基本思想

K＿means算法的基本思想是:首先從n個樣本集中隨機選擇K個樣本作為初始聚類中心，根據每個樣本與各個聚類中心的相似度，將其分配給最相似的聚類中心，得到K個互不相交的類簇集合；然后重新計算每個類簇的新中心，再將每個樣本根據相似性原理分配給最近的簇中心，重新計算每個類簇的新中心，分配每個樣本到距離最近的類簇。這個過程不斷重復，直到各個類簇的中心不再變化，得到原始樣本集合的K個互不相交的穩定的類簇。

該方法在聚類過程中采取距離就近原則，將數據樣本中的每個屬性變量統一看待，而忽略了每個屬性在聚類分析過程中對于數據樣本劃分的不同重要性。例如在發動機狀態評估中，特征序列與使用時間序列的相關性越大，表示特征參數隨使用時間逐漸劣化的趨勢越明顯，用來評估發動機技術狀況優劣的效果越好，在聚類過程中應給予相應重視。

由于K＿means算法是一個局部搜索過程，其聚類結果依賴于初始聚類中心和初始劃分[5]，因此本文中提出基于加權歐氏距離最小方差優化初始聚類中心的K＿means改進算法。

1.2 K＿means算法一般過程

在K＿means算法中，對于待聚類的數據樣本X＝(x1，…，xn)和 K 個初始聚類中心 C1，C2，…，CK，基本定義如下。

樣本xi與xj間加權歐氏距離:

樣本xi到所有樣本的平均距離:

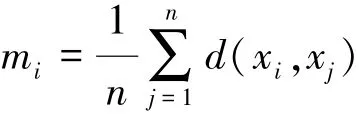
樣本xi的方差:

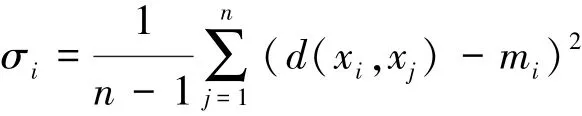
數據樣本的平均距離:

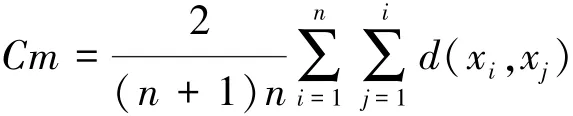
聚類誤差平方和:

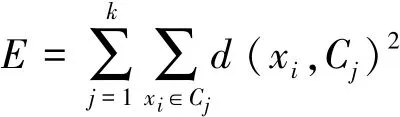
其一般過程如圖1所示。

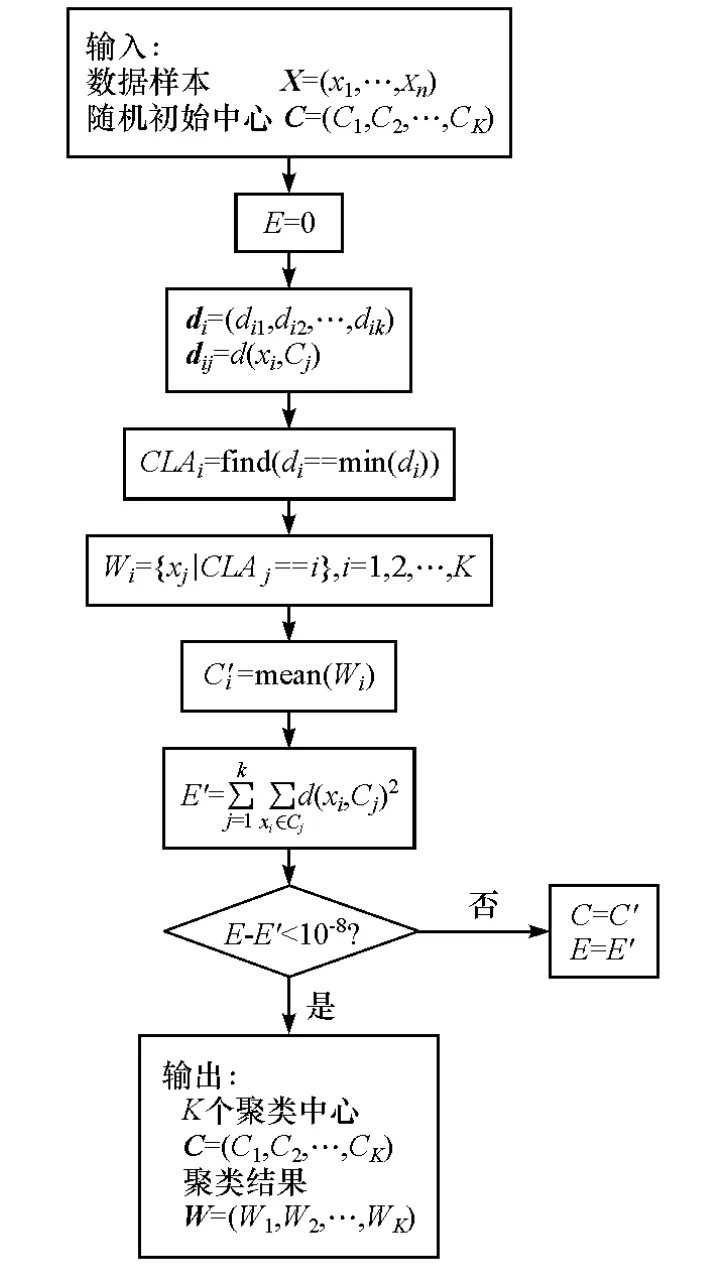
圖1 K＿means算法一般流程

2 算法改進

2.1 相關性加權歐式距離

在傳統聚類算法中，按樣本間相似度進行聚類劃分通常以歐氏距離為準，即

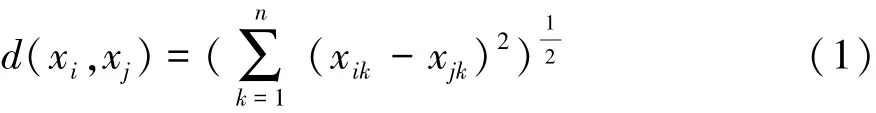
為了反映特征序列與使用時間序列的相關性，通過對多種賦權法的比較[6]，提出了基于特征序列相關性指標的定權方法。相關性指標是在相關系數的基礎上提出的，以取絕對值的方法將其限定在[0，1]區間，表征了特征序列與使用時間間的線性相關程度。某個特征序列的相關性指標值越大，其與使用時間的線性相關性也越大，從而該特征也能更好地描述發動機技術狀況從優到劣的變化過程。該方法權重計算步驟如下。

對于樣本數據的第i個特征序列，其相關性指標是其相關系數的絕對值，即

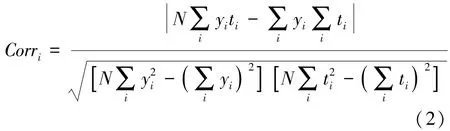
式中:Corri為第i個特征序列的相關性指標；Y＝(y1，y2，…，yN)為第 i個特征序列；N 為檢測次數，即序列長度；T＝(t1，t2，…，tN)為相應時間序列。 根據樣本所有屬性的變異系數，計算各屬性的權重:

此時計算樣本間相似度可采用加權歐氏距離:

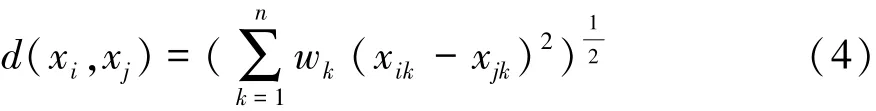
2.2 初始中心優化選取

由于樣本分布存在不確定性，傳統K＿means算法中依靠隨機選取產生的初始聚類中心，有可能是一些孤立點或噪聲點。這將導致聚類結果偏離真實分布，從而得到錯誤的聚類結果，并且這一現象在小樣本條件下的發動機狀態評估過程中將更加嚴重。因此本文中提出最小方差啟發式初始聚類中心優化選取方法。

該方法的基本思想是:以樣本方差作為啟發信息，選取方差最小的樣本作為初始聚類中心，并以樣本平均距離劃分初始聚類，從而選擇出周圍樣本分布比較密集的初始聚類中心，避免孤點和噪聲點的干擾。算法流程如圖2所示。

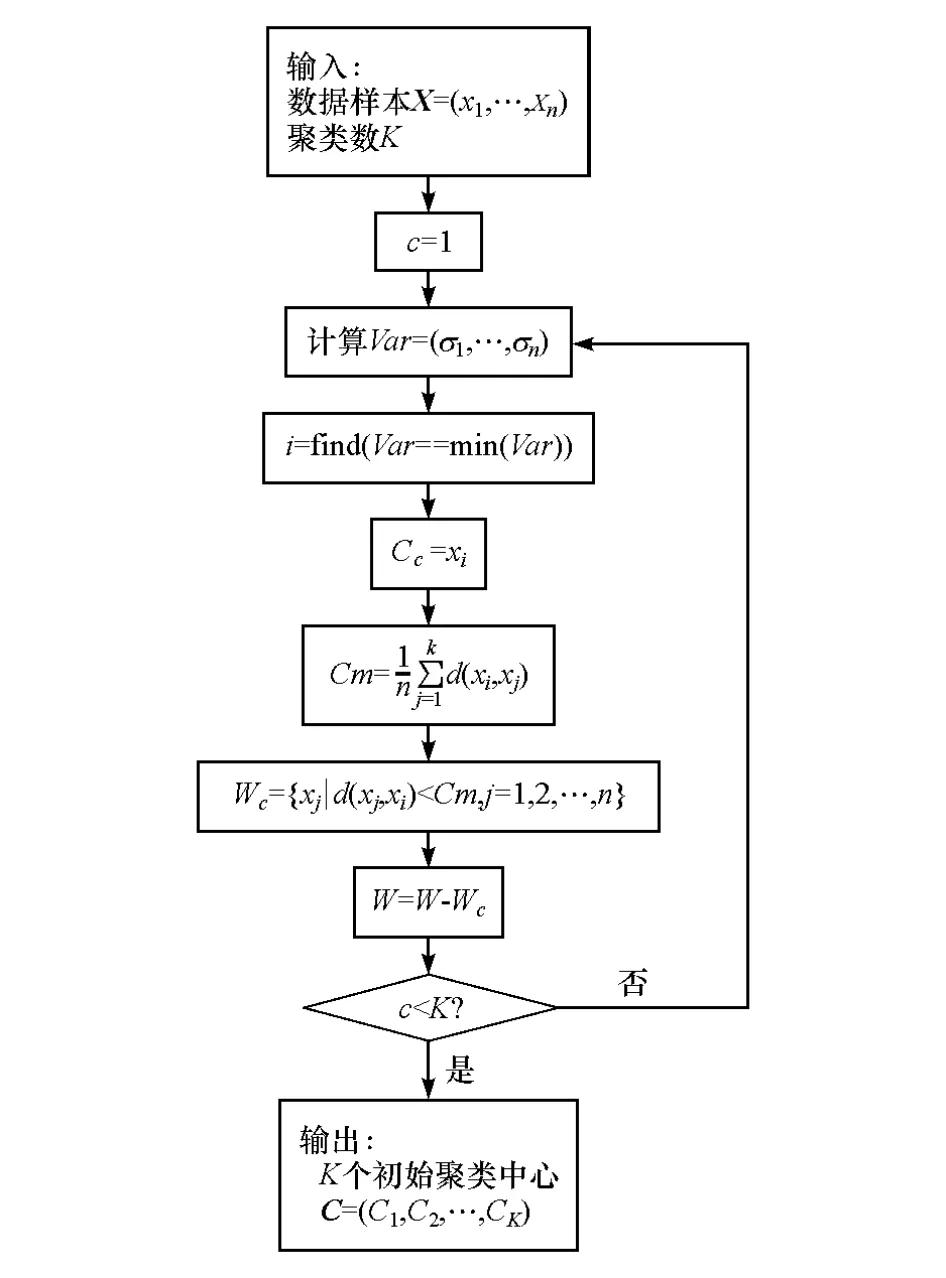
圖2 初始聚類中心計算方法

2.3 Bootstrap小子樣統計方法

Bootstrap小子樣統計方法是一種自助估計方法，其思路是用現有的資料去模仿未知的分布，通過再生抽樣將小樣本問題轉化成大樣本，因此該方法適用于小樣本條件下的統計推斷。

Bootstrap方法基本原理主要根據觀測到來自于未知總體分布F的隨機子樣X＝(X1，…，Xn)，估計總體分布F的某一分布特征R(X，F)，如均值、方差等，從而推測總體分布F，具體方法如下。

設總體分布F的某個分布特征θ＝θ(F)(如均值，方差等)，由觀測子樣 X＝(X1，…，Xn)構造經驗分布 Fn，則有對 θ的估計 θ＾＝θ＾(Fn)，估計誤差為

根據經驗分布 Fn，重新抽取再生子樣X(1)＝(X(11)，…，X(n1))，進而構造經驗分布函數F(n1)。于是由X(1)又可得到θ的估計F(n1))。此時可得到估計誤差Tn的Bootstrap統計量R(n1)，即

重復抽取多組再生子樣 X(i)，i＝ 1，2，…，m，可計算相應的R(ni)，i＝ 1，2，…，m，進而可利用 R(ni)的分布去逼近Tn的分布，即可根據式(1)得到θ(F)的樣本:

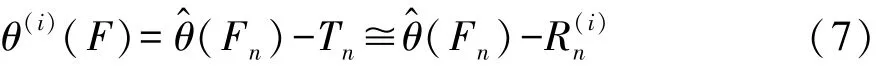
在小樣本估計中，該方法較傳統統計方法具有較高精度。

3 發動機狀態評估實例

3.1 評估樣本數據采集整理

以某型裝甲車輛柴油機為研究對象，其常用的技術狀況評估指標體系如圖3所示[7]。對累計使用時間在0～550摩托小時內的發動機，盡量按每間隔50摩托小時選擇1臺作為基準樣本，同時選取3臺狀態已知的發動機作為測試樣本，以驗證方法的有效性。采集處理后部分樣本狀態參數如表1和表2所示。

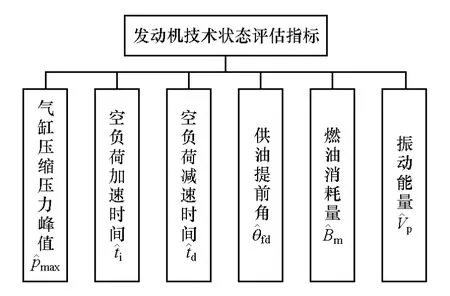
圖3 某型裝甲車輛柴油機評估指標體系

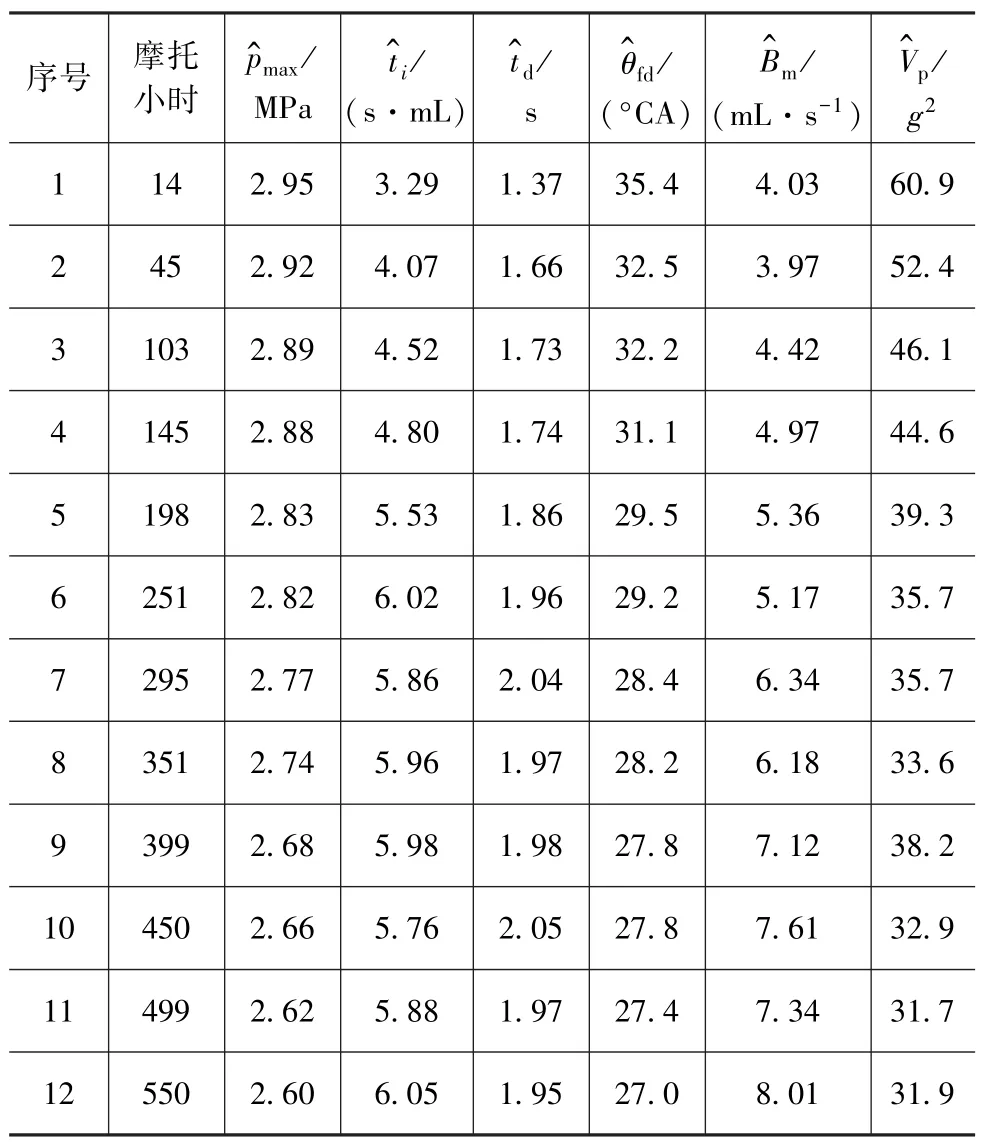
表1 基準樣本狀態參數

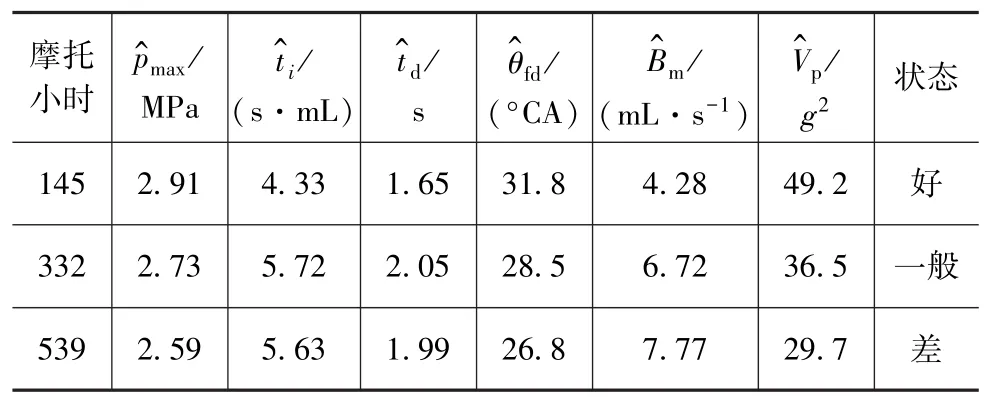
表2 測試樣本狀態參數

3.2 發動機狀態評估步驟

(1)評估數據選取

在實例驗證中，表1樣本為基準樣本，建立發動機狀態評估模型，劃分各技術狀況等級基準；選取表2樣本為測試樣本，利用上述模型評估其技術狀況，以驗證該方法的有效性。

(2)確定評語集

根據柴油機技術狀況的優劣程度，建立5級評語集。 將柴油機劃分為“好”、“較好”、“一般”、“較差”和“差”5個技術狀況等級。

(3)計算各屬性權重

根據表1所示樣本數據，計算特征參數對應的變異系數:

V＝[0.116，0.482，0.353，0.280，0.724，0.687]

由式(3)可得各屬性權重:

W＝[0.044，0.182，0.134，0.106，0.274，0.260]

(4)初始聚類中心

對于發動機而言，由于出廠后需要經歷一定時間的磨合，磨合期結束后發動機狀態達到最佳，發動機達到規定使用時長的極限，返廠大修時，其狀態為最差。因此在采用K＿means聚類算法時，可直接采用磨合期結束時(約50摩托小時)和返廠大修規定摩托小時(約550摩托小時)的樣本數據xi和xj分別作為“好”和“差”兩個等級的初始聚類中心，并根據其他樣本數據，采用圖1所示算法流程，計算“較好”、“一般”和“較差”3個技術狀況等級的初始聚類中心。

(5)分配樣本、更新聚類中心

將測試樣本依據式(4)分配到距離最近初始聚類中心相應的簇類中，并根據圖2的流程，重新計算聚類中心。更新后聚類中心矩陣為

(6)聚類中心修正

根據原樣本分布，重新抽取N組再生子樣X(n)，n＝1，2，…，N。 并對再生子樣重復步驟(4)和步驟(5)，計算相應聚類中心根據式(6)可知原樣本聚類中心的估計誤差分布為

本文中取N＝50重新抽取再生子樣，依照上述方法估計測試樣本聚類中心的誤差分布矩陣:

依據Bootstrap小子樣統計方法，可利用再生子樣修正原樣本各技術狀況等級的聚類中心:

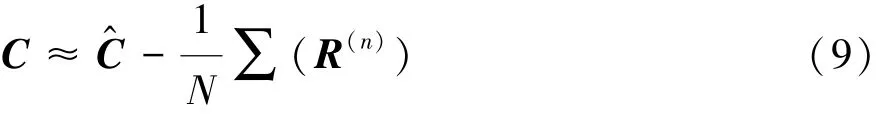
根據式(9)可得修正后聚類中心:

(7)樣本狀態評估

利用權重向量V和聚類中心C，根據相似性原理評估13～15號樣本的技術狀況，測試樣本對各等級基準的相似度和評語如表3所示。

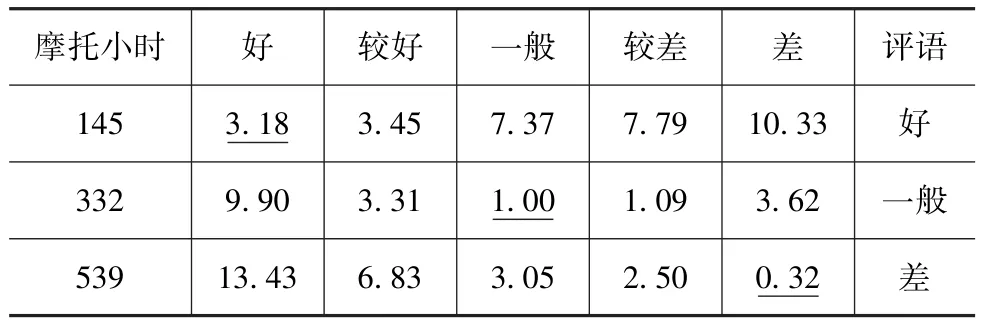
表3 測試樣本評估結果

測試樣本的評估結果能夠定量、定性地反映發動機技術狀況，并且與發動機實際狀況一致，因此該方法可作為在缺少先驗知識和小樣本條件下對發動機進行狀態評估的有效手段。

4 方法對比分析

為對比本文方法與文獻[3]中所述傳統方法的客觀性和穩定性，在上文1～12號基準樣本的基礎上，以相同方法重新采集整理一組對比樣本，如表4所示。

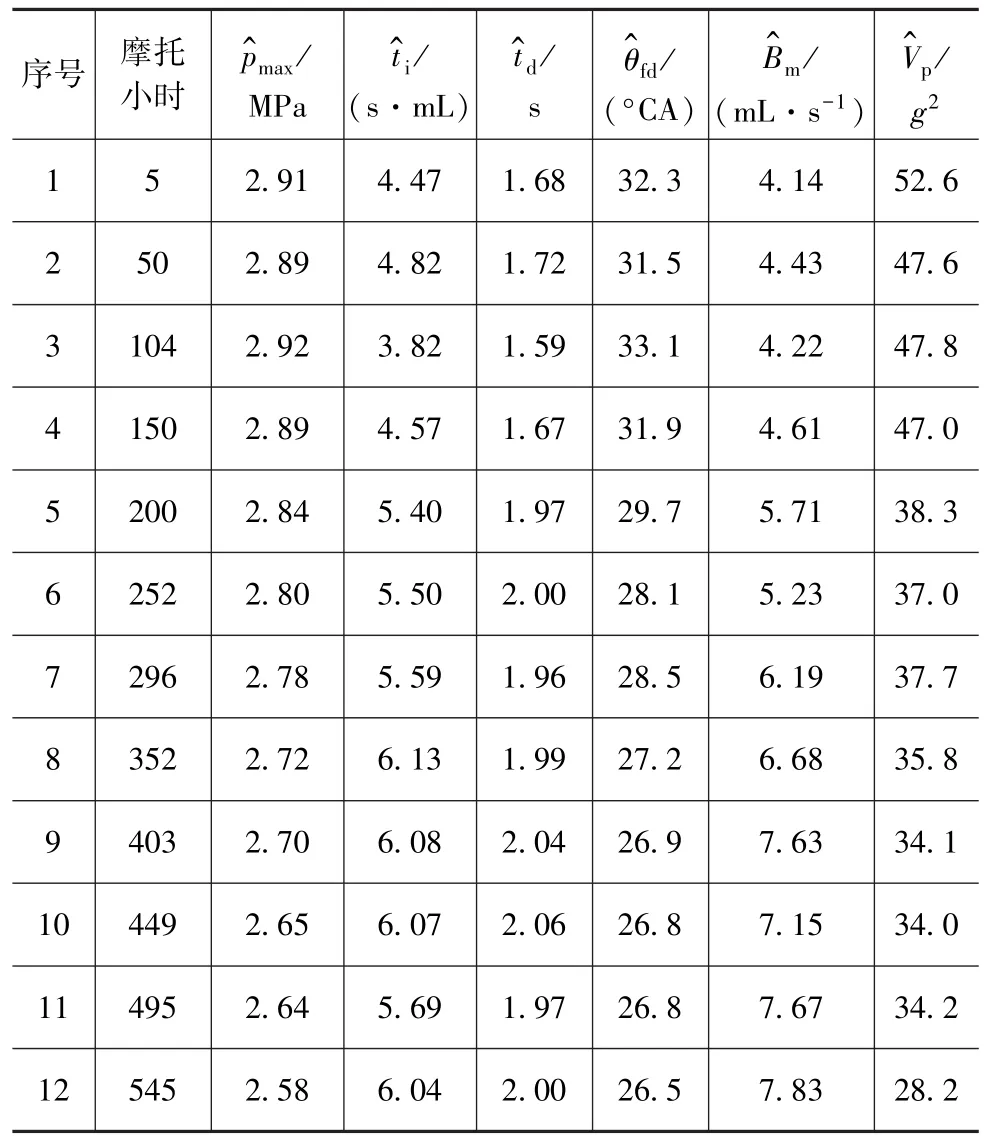
表4 對比分析樣本

采用本文提出的基于狀態參數方法，分別以第1組和第2組樣本建立評估模型，并對所有樣本進行評估，結果見圖4。

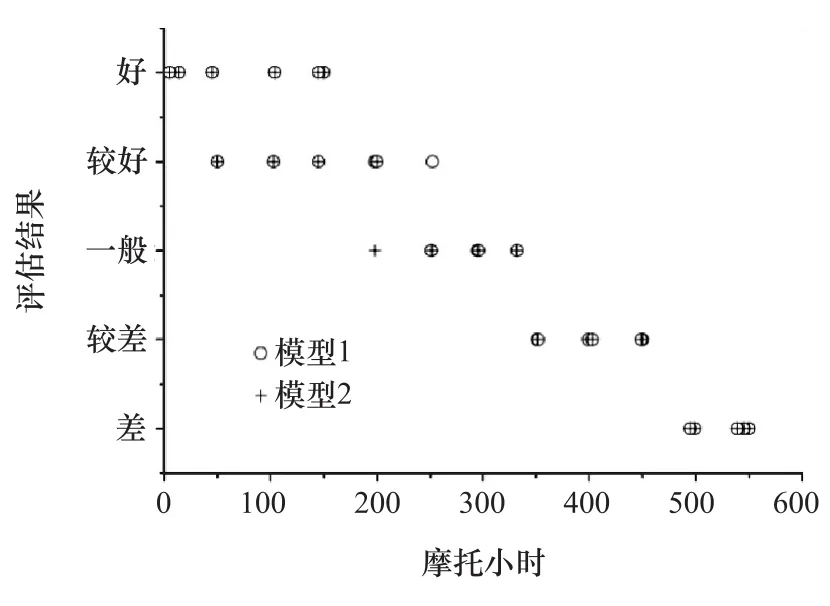
圖4 本文方法的評估結果

由圖可見:發動機的技術狀況隨著摩托小時逐漸劣化的趨勢明顯；在0～200摩托小時內基本為“好”和“較好”，在200～350摩托小時內基本為“較好”和“一般”，在這兩個區間內技術狀況呈現了兩種技術狀況變化的過渡，體現了技術狀況變化的逐漸性和模糊性；在350～450摩托小時內為“較差”，在500摩托小時以上為“差”。技術狀況的這種變化趨勢與理論分析的結果大致吻合。

采用文獻[3]中所述傳統方法，分別以第1組和第2組樣本建立評估模型，并對所有樣本進行評估，結果見圖5。

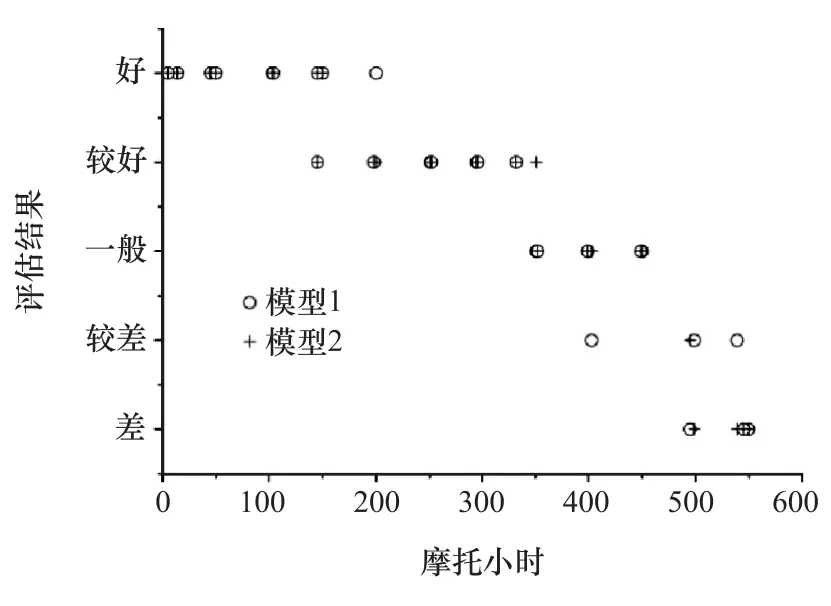
圖5 傳統方法的評估結果

用傳統方法評估所有27個樣本時，有6個樣本在兩組不同樣本建立的評估模型下的結果不同。而本文方法在相同條件下只有2個樣本得到了不同結果。這表明本文中提出的基于狀態參數發動機狀態評估方法在處理少量狀態參數樣本時比傳統方法具有更強的穩定性。

5 結論

本文中利用加權歐氏距離和最小方差啟發式算法對K＿means聚類算法進行了改進，并通過融合Bootstrap小子樣統計方法提出了一種基于改進K＿means的發動機狀態評估方法。

該方法能在缺少先驗知識的小樣本條件下，建立穩定的發動機狀態評估模型，實現發動機技術狀況的有效評估。與傳統方法相比，該方法在處理隨機性較大的狀態參數樣本時具有更強的穩定性，并且該方法完全依靠發動機狀態參數，具有更強的客觀性。