正項級數學習中常見的幾個問題
2018-08-20 05:10:08盧蘭
考試周刊 2018年76期
關鍵詞:問題

摘 要:正項級數在級數中是重要的理論基礎,本文主要針對學習正項級數時會出現的一些常見問題進行了歸納總結。
關鍵詞:正項級數;收斂;問題
級數是高等數學的重要章節,它不但能夠描述許多自然現象和工程技術中的客觀規律,而且可以近似計算無理數。正項級數作為級數重要的基礎理論,在解決很多級數問題中起著非常重要的作用。這節的內容比較多,關系復雜,很多初學者在學習過程中,存在很多疑惑,現將其歸納幾個問題如下:
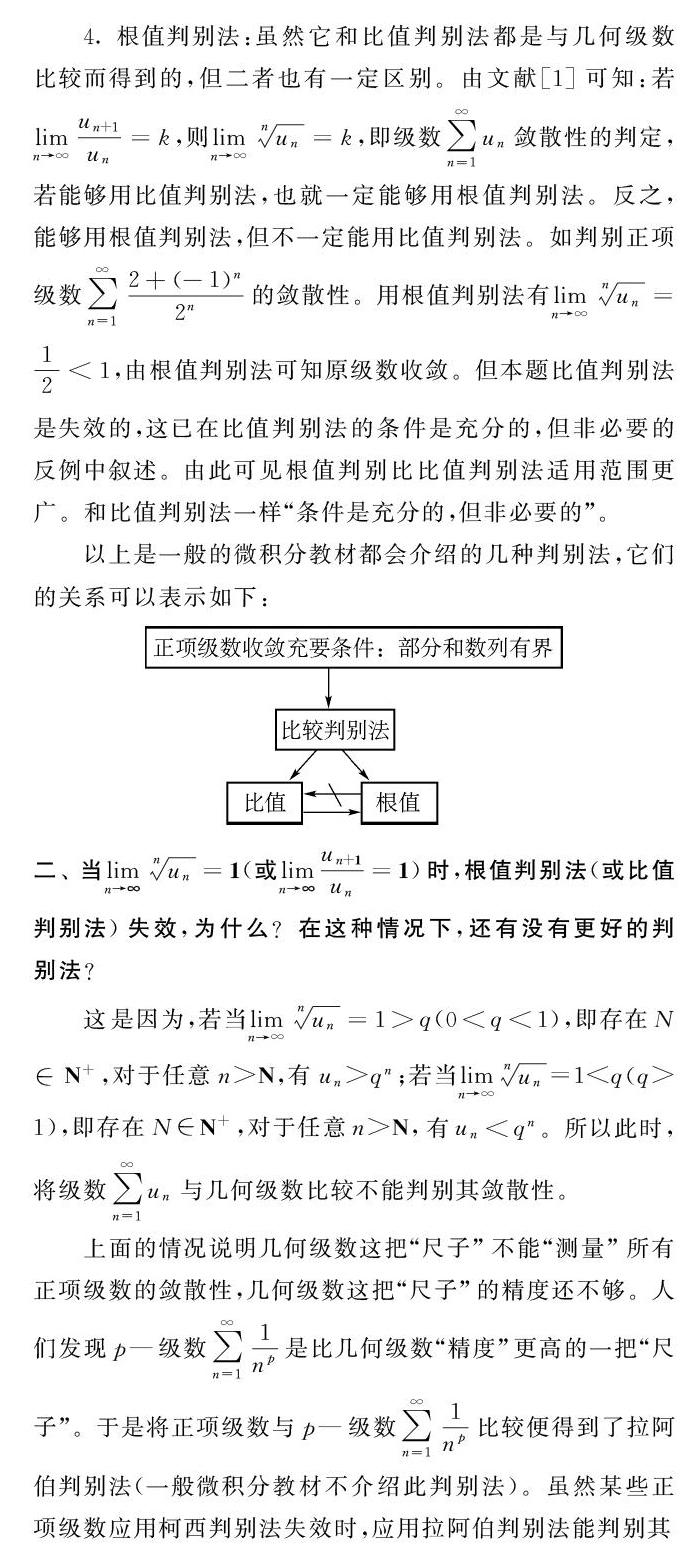
一、 判別正項級數斂散性的方法一般有哪些?它們有哪些優缺點?它們之間有何關系?
1 正項級數收斂的充要條件是它的部分和數列有上界。這是正項級數斂散性判別法的理論基礎,它的結論雖然完美,但應用起來往往困難。因此在它的基礎上人們研究出了一些更具體、更有針對性的判別法。
2 比較判別法:它有不等式形式與極限形式兩種表達形式,其中極限形式在解題中用起來比較方便。比較原則的基本思想就是通過與某一個正項級數(斂散性已知)的比較來確定另外一個正項級數的斂散性。這也是比較判別法的一個缺點,即須有參考級數的斂散性。常用的參考級數:(1)幾何級數,(2)P-級數,(3)調和級數。
三、 判別正項級數的斂散性一般程序是什么?
正項級數斂散性的判別程序一般如下圖:
有時候一個級數斂散性的判定是一個復雜的過程,單純地使用一種判別法往往是不夠的,需要級數的性質和幾種判別法并用方可解決問題。
參考文獻:
[1] 劉玉蓮,傅沛仁.數學分析講義[M].北京:高等教育出版社,1996.
[2] 關汝華,孟凡洪,劉家春.微積分[M].長春:東北師范大學出版社,2012.
[3] 同濟大學數學教研室.高等數學[M].北京:高等教育出版社,2004.
作者簡介:盧蘭,吉林省長春市,長春光華學院基礎教研部。
猜你喜歡
科技視界(2016年20期)2016-09-29 12:22:45
科技視界(2016年20期)2016-09-29 12:14:21
大眾理財顧問(2016年8期)2016-09-28 14:02:50
大眾理財顧問(2016年8期)2016-09-28 14:00:00
大眾理財顧問(2016年8期)2016-09-28 13:57:10
大眾理財顧問(2016年8期)2016-09-28 13:54:19
環球時報(2016-07-15)2016-07-15 13:42:04
環球時報(2016-03-09)2016-03-09 09:10:24
南方周末(2015-05-07)2015-05-07 04:39:36

