合理轉換圖形，巧解線段最值
——對一道中考題的解法分析與探究

☉江蘇省沛縣教師發展中心 甘 磊

一、考題再現及思路突破

1.考題再現

（1）試證明AC是⊙O的切線；

（2）如果點F是線段AO的中點，OE=3，試求圖1中陰影的面積；

（3）在條件（2）成立的情況下，已知點P是BC邊上的一個動點，當PE+PF取得最小值時，請直接寫出BP的長.

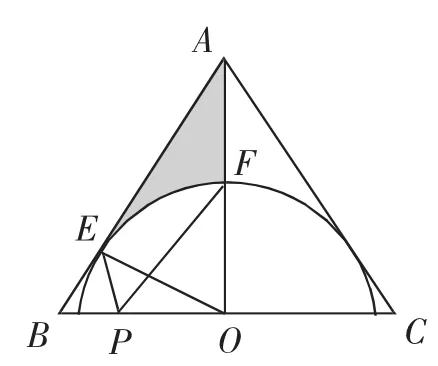
圖1

2.思路突破

分析：本題目為常見的幾何問題，涉及到圓和三角形等基本圖形，求解需結合基本的幾何知識.（1）證明切線可以過點O作AC邊上的垂線，如垂線為OM時，只需證明OM與圓的半徑相等即可；（2）陰影部分的圖形不規則，可以將其視為△AOE中切去扇形OEF獲得的，即S陰影=S△AOE-S扇形OEF，然后分別利用面積公式求出△AOE和扇形OEF的面積即可完成求解；（3）在（2）的條件下求PE+PF的最小值時的BP長，實際上就是求點P的具體位置，可以作關于線段BC，點E的對稱點G，連接FG，則此時FG的長度就是PE+PF的最小值，FG與BC的交點就是滿足條件的點P的位置，即可求出BP的長.

解：（1）過點O作AC邊上的垂線，垂足為點M，如圖2.因為AB=AC，AO⊥BC，則∠BAO=∠CAO，又知OE⊥AB，OM ⊥AC， 則 △AEO?△AMO，故OE=OM.因為OE為⊙O的半徑，所以OM同為⊙O的半徑，則AC是⊙O的切線.

（2）S陰影=S△AOE-S扇形OEF，其中

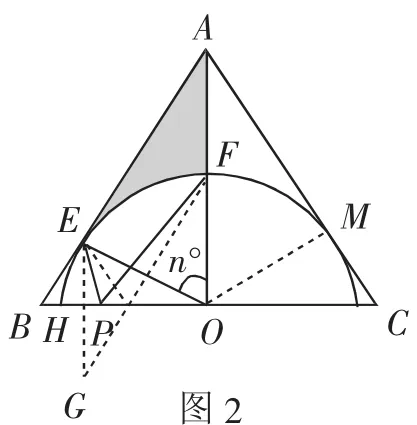
圖2

（3）作點E關于線段BC的對稱點G，連接EG交BC于點H，連接FG交BC于點P，可知EP=GP，由于點G、P、F處于同一直線上，則此時的PE+PF最小.在Rt△EHO中，EH=EOsin∠EOH=，BH=，△EHP～△FOP，則2HP=OP.又因為HO=HP+OP，可得HP=，所以BP=BH+HP=.

執行難，一直是司法實踐中的困擾。生效的裁判文書得不到執行，法院判決就成了一紙空文。“用兩到三年時間基本解決執行難問題”，最高人民法院鏗鏘有力的承諾不斷轉化為人民法院向執行難宣戰的切實行動。探索審判權和執行權分離，改革執行體制機制，聯合多部門對“老賴”進行信用懲戒，“法律白條”不斷被兌現為“真金白銀”。

3.考題評析

題目中是中考典型的幾何綜合題，圖形由三角形和半圓綜合而成，前兩問是常規的證明和陰影面積求值問題，分別利用垂線段與圓半徑相等和面積的割補法來完成，難度適中.問題第（3）問求PE+PF取得最小值時BP的長，需要確定點P的位置，屬于三點之間線段的最值問題，求解時將位于不同直線上的兩條線段通過軸對稱的方式轉化到同一直線上，從而確立了線段和的最小值，問題中隱含著研究線段和的最值模型，下面將深入探究.

圖3

二、最值研究模型的探究

1.教材模型

考題第（3）問基于幾何轉化思想，利用軸對稱變換的方式來解決線段和的最值，其利用的理論依據是：兩點之間，線段最短.該問題模型與教材中常見的水廠選址問題相類同：如圖3,在一條小河的同一側有兩個村莊A和B，現要在小河邊建一座自來水廠為兩個村莊供水，如果要使廠址到兩個村莊的供水管道最短，那么廠址應選在什么位置，試說明理由？

教材問題需要確定廠址的位置，若設廠址為P，則需要確保AP+BP的值最小，與考題在本質上是相同的，即有著同樣的問題模型，具體的做法是：將小河抽象為一條直線，作點A關于線段l的對稱點A1，連接A1B，與直線l相交于點P，如圖4，此時AP+PB取得最小值，則點P就為自來水廠的最佳選址.

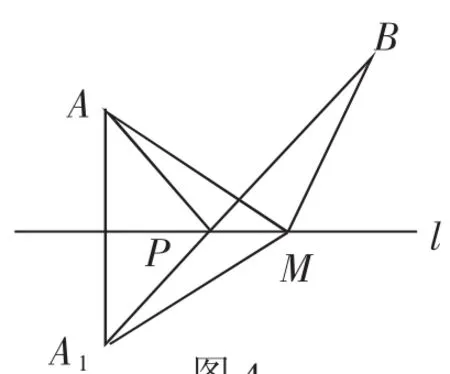
圖4

2.思路分析

通過軸對稱轉化的方式可以確定AP+PB取最小值時點P的具體位置，可以在直線l上構造異于點P的一點M來分析：取一點M，同樣連接AM和MB，在△BMA1中，BM+A1M＞A1B.因為A1B=A1P+PB，則BM+A1M＞A1P+PB，根據軸對稱的特性可知，AM=A1M，AP=A1P，則有BM+MA＞AP+PB，因此異于點P的一點M獲得的線段和大于點P獲得的線段和，可知軸對稱轉化的方式可以獲得線段和的最小值.

三、線段和最值問題的探究

考題的線段和問題可以等效為固定直線上一動點P，求定點E、F與動點P之間的距離和PE+PF的最小值，屬于三點之間的線段和的最值問題，在動點形式和解法上都具有一定的代表性，同時近幾年的中考題也都基于上述兩點來進行考查，現結合2018年中考題分別從問題條件和問題解法兩個方面進行變式探究.

1.問題條件變式

中考題中關于線段和的最值問題具有多種形式，上述考題中的三點具體為兩點固定、一點移動，也可以將其變為一點固定，兩點運動，同樣求解線段和的最值，現結合考題分析.

（2018年廣東廣州市中考卷第23題）如圖5所示，在四邊形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD.

（1）利用尺規作∠ADC的平分線DE，交BC于點E，連接AE（保留作圖痕跡，不寫作法）.

（2）在（1）的條件下，①證明：AE⊥DE；②如果CD=2，AB=4，點M，N分別是AE，AB上的動點，求BM+MN的最小值.

分析：主要分析第（2）問的②，問題中的點M，N分別是AE，AB上的動點，求其最小值同樣可以利用軸對稱轉化的方式，作點B關于線AE的對稱點F，當點F、M和N位于同一直線，且FN⊥AB時，如圖6，BM+MN可取得最小值，只需求得相關線段即可.

解：（2）②過點D作DP⊥AB，垂足為點P，作AD上取一點F，使得CD=DF，由1可知此時AF=AB，即點B、F關于直線AE對稱，過點F作AB的垂線，垂足為N，令FN交AE于點M，連接BM，此時BM=FM，點F、M和N位于同一直線，且FN⊥AB，此時BM+MN有最小值，且BM+MN=FM+MN，分析可知，△AFN～△ADP，則=，其中AF=4，AD=6.在Rt△APD中，可以求得DP=4，則FN=，即BM+MN的最小值為

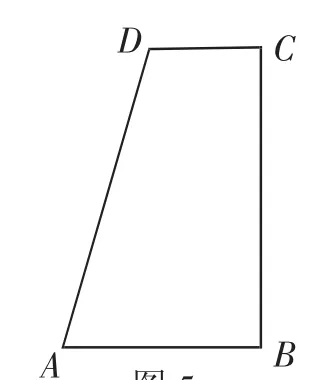
圖5

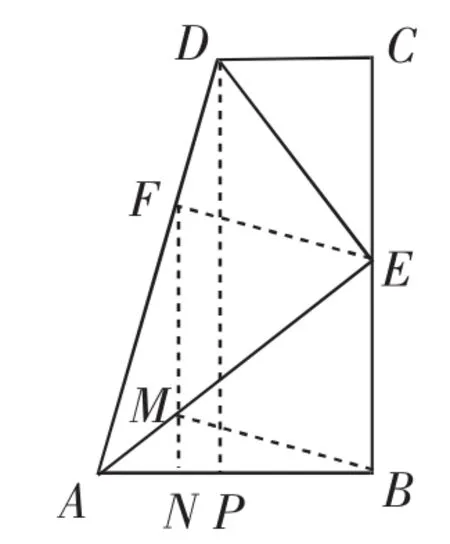
圖6

上述考題同樣是求三點之間線段和的最值，所不同的是存在兩個動點，但同樣可以依據“兩點之間，線段最短”的原理，通過軸對稱轉換的方式來求解.在細節處理上首先選定其中一動點所在直線為頂點與另一動點的對稱軸，并確定其中一動點的位置，然后連接兩點確定對稱軸上的另一動點的位置，從而使三點位于同一直線上，進而確定線段和的最小值.該種思路可以用于存在兩動點的線段和最值求解.

2.最值解法上的拓展

對于線段和的最值問題，除了可以采用軸對稱轉換的方式還可以采用等效轉換的方式，即通過線段長度等效的方式，將位于不同直線上的線段在同一直線上進行長度等效，轉化為兩點之間的距離，然后依據條件來確定線段和的最值，該種解法在考題中也有體現，下面結合考題詳細講解.

（2018年江蘇無錫市中考卷第18題）如圖7所示，已知∠XOY=60°，點A位于邊OX上，且OA=2，過點A作AC⊥OY于點C，以AC為一邊在∠XOY內作等邊三角形ABC，點P是△ABC圍成區域（包括各邊）內的一點，過點P作PD∥OY，交OX于點D，作PE∥OX，交OY于點E，設OD=a，OE=b，則a+2b的取值范圍是__________.

分析：求a+2b的取值范圍，就是求EP+2DP的最值，其中點P是△ABC圍成區成內的一動點，可以先對a+2b進行變形，即a+2b=2 （a +b），可以在OC的延長線上取一點H，使得EH=a，則a+b=EH+OE=OH，且三點均位于同一直線上，由于點O固定，則可以通過研究點H距O點的距離來確定線段和的取值范圍.

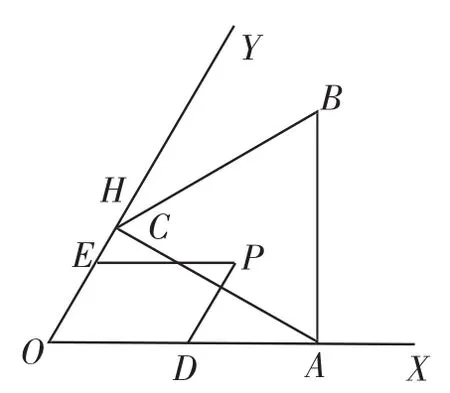
圖7

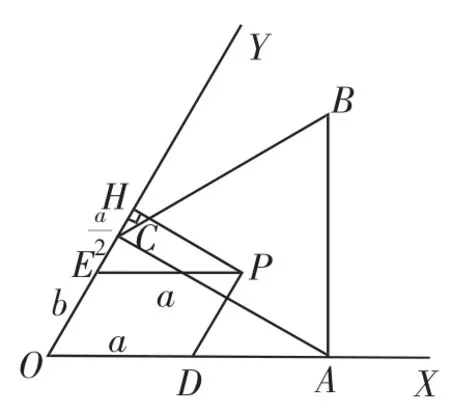
圖8

解：過點P作OY的垂線PH，垂足為點H，如圖8，在Rt△EHP中，∠PEH=60°，EP=a，則EH=a，a+2b=2（a+b）=2（EH+OE）=2OH，由于點P位于△ABC圍城區域內，則當點P運動到C點時，OH的長度最短，即a+2b取得最小值，2OHmin=2OC=2，當點P運動到B點時，2OH的長度最長，即a+2b取得最大值，此時2OHmax=2（OE+EH）=2×（1+）=5.所以a+2b的取值范圍為2≤a+2b≤5.

上述考題采用的是對線段長度的等效轉化，即在同一直線上取截問題研究的兩線段長，將其合并為同一線段，實現三點共線，利用的是同一直線上研究兩點之間距離最值的便利性，同時在求解時對線段和進行了一定的變形處理，并用點距離來表示，使得分析問題更為直觀.

四、解后思考，學習建議

線段和的最值問題，實際上幾何中的動點問題，由于進行求和的兩條線段位于不同的直線上，因此無論是軸對稱變換法，還是長度等效轉換法.實際上都是為了將兩條線段轉換到同一直線上，雖轉換形式不同，但都是數學轉化思想的利用.學習使用上述兩種方式時首先需要透徹理解方法的實質，如軸對稱轉換，建立關于直線的對稱點僅是解題的表面形式，實質上利用的是軸對稱所構成的三角形全等性質；而長度等效轉換則更為直接，就是在同一直線上進行的等長截取，方法的核心要素是長度等效，利用的是幾何性質來完成.

對于線段的求和問題，數形結合思想貫穿解題始終，具有兩種思想方法作指導：一是利用幾何圖形為導向直接建立問題求解的具體思路，然后利用代數方法來計算求解，即以形助數；二是基于代數對線段長度的精準表達意義來進行等效轉換，該種方式主要體現在長度等效轉換上，即以數解形.合理采用數形結合的解題方式，可以從抽象問題中提煉基本的模型，實現問題模型的準確分析.另外對于線段和的求值問題教材習題中有較為詳細的實例，合理抽象模型往往可以獲得豐富的解題經驗，利于考題的分析求解.

了解問題的基本模型，理解方法的核心思想，掌握解法的求解思路是求解線段和最值問題的關鍵，在平時的學習中除了需要學習方法，還需要鞏固基本的幾何知識，靈活運用，巧妙求解.