數列解題中易錯問題例析
山東省青島市城陽區第一高級中學 潘繼祥
數列是高中數學的重要內容之一,也是歷年高考數學考查的熱點之一,由于數列考查學生的綜合能力較強,學生在解題的過程中經常會因為定義公式不清、審題不細、忽略條件、思想方法考慮不周等原因而錯解題目。下面就一些常見錯誤分類例析如下。
一、對概念理解不透徹致誤
例1 已知數列{an}的前n項和為Sn,,求通項an。
錯解:由 Sn+1得 Sn-1+1,兩式相減得 ,則有=2,所以數列{an}為等比數列,又 ,所以 。
錯因分析:對等比數列的概念理解不透,由 Sn+1和忽視了n≥2,從而漏掉檢驗
正解:數列{an}從第二項起構成等比數列,所以當n≥2時,
例2 等比數列{an}中,已知an>0, ,求a5,a7的等比中項。
錯解:設該等比數列的公比為q,首項為a1,由題意得解得則的等比中項為3。
錯因分析:對等比中項的概念理解不透,誤認為a5,a7的等比中項為a6,要明確非0同號兩數的等比中項有兩個,且互為相反數。可設G為a5,a7的等比中項,則 ,所以a5,a7的等比中項為3或-3。故正確答案為3或-3。
二、公式應用錯誤致誤
例3 設等比數列{an}的前n項和為Sn,若,求數列的公比q。
錯因分析:錯誤在于用等比數列求和公式時忽視要分兩種情況q=1和q≠1討論,即當q=1時,則有 ,顯然,與題設矛盾,故q≠1;當q≠1時,解法如上。所以正確答案為
三、審題不細,抓不住問題的本質致誤
例4 已知等差數列{an},首項a1=5,前n項和為Sn,僅當n=10時Sn取最大值,求公差d的范圍。
錯解:因為僅當n=10時Sn取最大值,由等差數列單調性知前10項為非負,所以,
錯因分析:對等差數列的單調性理解不夠,由題意知此數列為遞減數列,僅當n=10時Sn取最大值,隱含條件為前面10項都大于0,沒有0項,所以由相鄰兩項 組成不等式組解得
例5 已知等差數列{an}的首項公差d>0,從第10項起每一項都大于1,求公差d的范圍。
錯因分析:對等差數列的單調性理解不夠,由公差d>0知此數列為遞增數列,從第10項起每一項都大于1,隱含條件為前面的每一項都小于等于1,所以由相鄰兩項 組成不等式組得
四、混淆數列與函數的思想方法致誤
錯因分析:上述解法忽略了數列中的項數n應為正整數這個條件。由于n∈N*,所以當n取距離最近的正整數2時,an取得最大值13。∴數列{an}中的最大項為a2=13。
例7 已知數列{an}是遞增數列且,求實數λ的取值范圍。
五、忽視分類討論思想致誤
例8 已知數列{an}的前n項和Sn=12n-n2。(1)求通項an;(2)求數列的前n項和Tn。
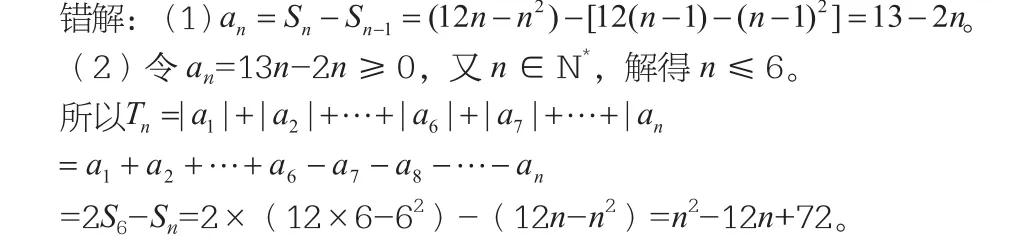
錯因分析:兩問都忽視了分類討論的思想,前者忽視了an=Sn-Sn-1只有n≥2時才能成立,當n=1時,a1=S1=12×1-12=11,也符合 an=13-2n,所以an=13-2n。后者忽視了對n的討論。
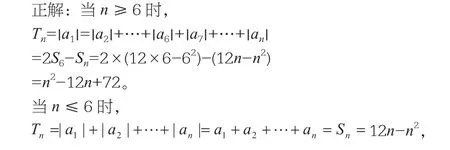

上面簡單地列舉了數列解題中常犯的一些錯誤,當然,易錯點遠不止這些。要想在解題過程中少出錯誤,我們首先要吃透定義與公式,掌握數列性質的內涵與外延,深刻理解數列所蘊含的數學思想。抓住問題的本質,揭示問題的內在聯系和隱含條件,明確解題方向,才能打通解題思路,同時做一些必要的針對性練習,記錄自己在練習中經常出現的錯誤并進行反思,這樣就能避免出現類似錯誤。

