以列方程組的思路求二次函數解析式
山東省菏澤市單縣高韋莊鎮中學 王志敏
二次函數是初中數學最基本、最重要的一個函數,這個函數解析式的變式比較多,而且是幾何與代數的綜合,所以涉及的知識點比較多。如果對相關知識不夠熟悉,看到這里出現這么多的字母,理解起來就比較困難。要求二次函數解析式,首先要明確目標,確定二次函數三個常數系數a,b,c的值,其次要了解三種表達式之間的關系:由一般式到頂點式,需要提取二次項系數并配方這個步驟;一般式與兩根式的關系是通過一元二次方程的解和韋達定理聯系起來的。而解三元一次方程組時,需要用到消元的方法,要想得到三個未知數的解,至少需要列出三個方程,所以要求得二次函數的解析式,我們就要列出以a,b,c為未知數的三個方程。
一、將一般式轉化成三元一次方程組求解
函數方程不僅是一種教學工具,而且也為函數教學提供了研究方法,是數學的一種研究手段。函數的定義是:在某變化過程中有兩個變量x,y,如果對于x在某一范圍內的每一個確定的值,y都有唯一確定的值和它對應,那么,就把y叫作x的函數。如果x的最高次數是一次,那么,這個函數就是一元一次函數;如果x的最高次數是二次,那么這個函數就是一元二次函數。一元指只含有一個未知數,因為初中階段只涉及一元函數,不涉及二元及多元函數,所以一元一次函數又叫一次函數,一元二次函數叫二次函數。
二次函數的基本表達式為一般式:y=ax2+bx+c(a,b,c為常數,a≠0),其中,a為二次項系數,b為一次項系數。
例如:已知一個二次函數過三個點(1,6),(2,11),(3,18),求二次函數解析式。
這個題的關鍵是要知道二次函數的每個點的表示方法是(x,y),也就是當x=1時,y=6;當x=2時,y=11;當x=3時,y=18。將三個點代入方程,就可以得到一個三元一次方程組:
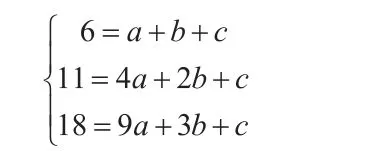
這個三元一次方程組通過消元,就可以得出a,b,c的值,進而列出二次函數解析式。
二、將頂點式轉化成方程組求解
當已知條件里面有頂點(最低點或最高點)時,就可以用二次函數的頂點式y=a(x-h)2+k(a,h,k為常數,a≠0)。需要注意:將頂點坐標代入頂點式后,就可以將二次函數變成只有一個變量a的函數y’,這時再代入另一個點的坐標就可以求出a,然后將a的值代入y’,最后將平方式展開整理,就可以得到二次函數解析式的一般式。
例如:已知二次函數的最低點是(2,3),并過(1,4)這個點,求二次函數的解析式。
這道題的關鍵是理解最低點的含義,最低點表示這條拋物線過(2,3)這個點,將點坐標代入二次函數的一般式y=ax2+bx+c(a,b,c為常數,a≠0)時是成立的。另一個已知條件是這條拋物線還過點(1,4),也就是說將這個點代入一般表達式也是成立的。
用二次函數的頂點式y=a(x-h)2+k(a,h,k為常數,a≠0),這個時候可以看到這個二次函數還是有三個未知數,不過,因為知道頂點,也就是h,k是已知條件,所以直接將h=2,k=3代入二次函數的頂點式,就可以得到y=a(x-2)2+3這個新函數。將(1,4)這個點代入后得到4=a(1-2)2+3,這個方程中只有一個未知數,解得a=1,將a=1代入y,然后將平方式展開整理,就可以得到二次函數的一般式。
三、將兩根式轉化成方程組求解
用兩根式求二次函數的解析式時,需要注意的是當函數值等于0時,二次函數變成了一個一元二次方程,x1和x2是這個方程的兩個解,兩根式與一般式之間的聯系是韋達定理,韋達定理的表達式是
例如:已知二次函數與x軸的交點是(1,0),(2,0),并且這個函數過點(3,2),求二次函數解析式。
我們可以看到這個題給出了三個點,因此可以列出二次函數的一般式y=ax2+bx+c(a≠0),將三個點直接代入一般式可以得到三個方程里面有三個未知數,通過消元,就可以得到a,b,c的值。

