以解簡單方程為例談小學數學試題命制

江蘇泰州市姜堰區第二實驗小學教育集團（225599）

試題的設計不僅要便于評價學生的學習情況，還要盡量反映學生的學習過程。那么，究竟該如何設計一份含金量較高的試題？對此，筆者特以“簡易方程”為例來分步討論。

一、關注“四基”，創建科學評估體系

根據“四基”的要求，教師在設計試題時應重視學生對知識的理解程度，讓學生運用所掌握的知識來解題，而不是通過套用概念或公式來解題。試題的設計應通過圖示來考查學生對知識的理解情況。

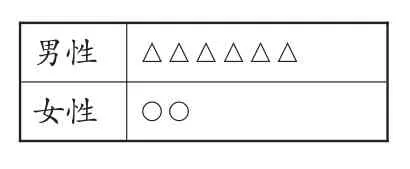
【命題1】表格表示某體育代表團有60名男性運動員，○=2△，則女性運動員有（ ）人。

【分析與思考】本題旨在考查學生的讀題能力。數學理解不僅是對字符和公式的理解，還有包括對表格、文字、統計圖等題目形式的理解。本題主要使用數形結合、符號代數、等量替換等策略來測試學生對方程本質的理解程度，讓學生經過一番分析、轉化后，靈活機動地解決問題。

【命題2】下面哪幅圖所示的數量關系能夠表示方程？（ ）

男性女性△△△△△△○○

【分析與思考】本題借助天平模型來考查學生對方程的理解情況，便于學生從“左右托盤等重”來類比“算式兩邊相等”，從而在整體上把握方程概念。本題有助于學生理解方程是等式的基本屬性，同時有助于學生感知利用等式性質解方程的好處。

二、回歸現實，靈活運用和多層轉化

要想檢測學生的真實水平，就要采用生活中的數學素材創設生動形象的問題情境，讓學生學會用嚴謹的態度和科學的方法解決問題，從錯綜復雜的問題表象中提煉出數學模型，進而發現問題背后的知識本質。

【命題3】上海到福建的航線全長約100千米，客機以200千米/時的速度直線飛行。

（1）飛行t小時后，客機離上海有（ ）千米。（用代數式表示）

（2）請給t賦值，計算出結果（ ）。（3小時 0.3小時0.003小時）

【分析與思考】本題主要考查以字母代替數字后，數量關系的表達。題目若沒有字母表示，數量關系就無法以算式的形式清晰展現。本題的問題設置促使學生將題干中的主要條件轉化為代數式，如此既培養了學生的數學歸納分析能力，也發展了學生的代數意識。

【命題4】大數據調查表明：正常人的體重與身高存在一定的比例關系。如用m表示體重（千克），用n表示身高（厘米），則有公式：n－105=m。若王阿姨的體重是58千克，她的身高應是（ ）厘米。

【分析與思考】這是一個全新的問題情境，學生接觸新問題時，需要經過分析推理。本題通過公式“n－105=m”簡明地表示出體重與身高的數量關系，學生在理解各字母含義的基礎上通過對m或n進行賦值，便可求出n或m的大小。

三、展現解題經過，體現知識內涵

試題考查的不僅是學生是否答題正確，還應考查學生的解題思路是否清晰。因此，教師在設計試題時應遵循學生的思維習慣，讓學生在解題過程中明確自己的解題思路。

【命題5】方程（24－3x）÷8=0與下列哪個方程同解？（）

A.3x=8 B.3x+8=24 C.24－3x=0 D.x=8

【分析與思考】傳統的試題比較重視解題結果，只要結果正確就可以推定學生的解題過程是完整的。本題考查的并非方程的解，而是考查學生在找同解方程的過程中是否嚴謹。

【命題6】一塊三角形瓷磚的面積是S，要鋪成右圖這樣的花紋，花紋面積是（ ）。

【分析與思考】本題不僅考查學生的觀察、分析和對比能力，同時也考查學生的空間想象能力和圖形切換能力。學生不同的解答過程反映出他們所具備的知識運用技能，能力強的學生可以直接算出結果；能力弱的學生則需要通過拼圖、切分、數數等操作才能解決本題。

綜上所述，教師命題時不僅要考慮能否考查出學生的學習技能與綜合素質，而且要考慮試題的科學性和技巧性，以便有效地發揮試題的測評功能。教師要努力讓多元化的課程目標融入試題中，以促進學生的全面發展。