理解，數學教學的應然追尋

江蘇徐州市銅山區黃集實驗小學（221145）

《義務教育數學課程標準（2011年版）》指出：“課程內容的選擇要貼近學生的實際，有利于學生體驗與理解、思考與探索。”數學理解就是從生活經驗表象中抽象出數學知識的過程，可以促進學生知識的遷移，讓學生對知識做到“知其然且知其所以然”。那么，如何促進學生的數學理解，提升學生的思維品質呢？筆者從自身的教學實踐出發，進行了積極的探索。

一、建立新知的基本模型，鋪設數學理解的基石

皮亞杰指出：“數學知識是以一定的內在的邏輯組織起來的結構系統。”學生學習新知的過程，就是把新知與自身已有的知識經驗進行對比，然后不斷抽象、提煉，將其內化到自身的認知結構中的過程。在實際的數學學習中，學生更多會關注知識的局部散點狀態，對數學知識的學習往往處于線性的積累狀態，缺乏整體的把握。有的新舊知識之間的聯系非常密切，舊知能自然生長出新知，新知又涵蓋了舊知，知識的遷移自然而無痕跡；有的新舊知識之間的聯系不緊密，恰處于知識的區分點，這類新知往往不易于學生理解。因此，教師應從學生的數學理解出發，關注知識之間的邏輯關系，從整體結構上引導學生建立新知的認知模式，促進學生深層次的數學理解。

如教學蘇教版教材三年級“小數的初步認識”時，由于缺少相應的知識聯系支撐，學生由整數的認識向小數的認識遷移時遇到困難。教師可先通過創設研究課桌的長和寬的長度的情境，揭示引入小數的必要性，感受一位小數與十分之幾的聯系，體會一位小數的含義；接著，引入生活中購物的情境，激活學生的日常生活經驗，讓學生在熟悉的商品價格的基礎上認識小數，然后觀察小數與以前學過的數的不同之處，形成“鉛筆的價錢0.6元就是6角”的認知，并從元和角的進位關系理解零點幾元的含義。通過“圓珠筆的價格是1元2角，就是1.2元”之類的問題，激活學生已有的生活經驗，明確幾元幾角可以改成用“元”作單位的小數，明確“十分之幾可以寫成一位小數，一位小數表示十分之幾”。通過豐富的生活經驗建立促進學生理解的數學模型，不僅給學生的認知提供了起點和支撐點，還為學生進一步探究數學知識打下了知識基礎和方法基礎。

二、構建準確的知識表象，深入數學理解的核心

知識表象，就是學生對抽象的知識的直觀感知，它具有概括性和可描述性。構建準確的知識表象，就能快速地回憶和提取，便于思維集中于問題解決的關鍵點，使學生的數學理解更有效。知識表象的構建，是一個不斷深化、提升、糾正和精確的過程。在這個過程中，學生經歷觀察、操作、想象、思考，不斷把生活經驗表象化，促使思維逐漸走向深刻。

如教學蘇教版教材四年級“三角形的認識”時，教師引導學生通過操作，體會三角形的特征，促使學生把隱性的認知建構為準確的知識表象。教師在方格紙中畫出4個點（如下圖），要求學生先選擇3個點連成三角形，探究一共有多少種不同的方法，使學生的空間能力得到提升，然后思考可以去掉哪個點，使得剩下的3個點仍能連成三角形，讓學生明白，構成三角形的3個點不能在同一條直線上，深化學生對三角形的認識。

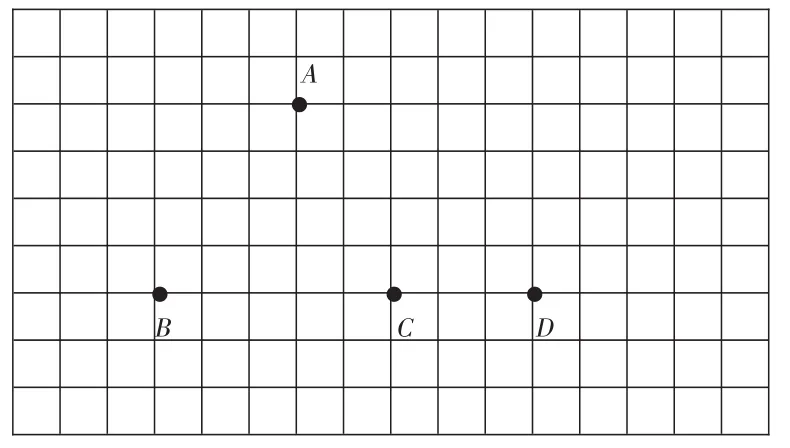
通過數學活動，讓學生體驗和感悟數學知識的形成過程，順應了學生的思維，同時讓學生建立起清晰的知識表象，使學生收獲知識與技能。學生通過實驗操作，深刻理解了知識的本質特征，提升了認知水平和數學思維品質。

三、著眼知識之間的聯系，夯實數學理解的根本

數學學習，是把從外部獲取的數學材料進行加工、整理，并內化到認知結構的過程。這個過程中，需要找到新知與原有知識之間的相同點和不同點，建立緊密的知識聯系，才能形成良好的認知結構。教師應著眼知識之間的聯系，從學生的認知實際出發，促使學生親歷知識的發生和發展過程，感悟其中的基本數學思想，積累活動經驗，引領學生的思維發展。

如教學蘇教版教材四年級“三角形三邊的關系”時，教師先引導學生動手實踐，讓學生感悟到數學來源于生活，然后通過觀察、分析、猜想、計算、比較、驗證等數學活動，培養學生的空間觀念、數學理解能力、合情推理能力以及抽象概括能力。

教師給每個小組（2人）提供了分別長3厘米、4厘米、5厘米和8厘米的小棒各1根，讓學生用其中的3根圍三角形。在交流時，教師讓學生說出哪些小棒能圍成三角形，哪些不能圍成三角形。

生1：3厘米、4厘米和5厘米的小棒以及4厘米、5厘米和8厘米的小棒這兩組小棒可以圍成三角形，而3厘米、4厘米和8厘米這個組合的小棒不能圍成三角形。

師：3厘米、5厘米和8厘米這組小棒能圍成三角形嗎？

（出示學生的圍法，不能圍成三角形）

師：為什么這組小棒不能圍成三角形呢？

生2：其中兩根小棒不能首尾相接。

師：看來3根小棒能不能圍成三角形也是有條件的。仔細觀察剛才的4組數據，你有什么發現？

（學生觀察、交流，得出結論：三角形任意兩邊的和大于第三邊）

教師從學生已有認識出發，讓學生通過圍三角形的活動獲取直接的數學活動經驗，培養了學生分析數據、推理和數形結合的意識。

四、組織合理的認知結構，促進數學理解的升華

數學知識的學習過程，就是學生組織、內化和完善認知結構的過程。隨著活動體驗的深入，學生的活動經驗不斷豐富，認知不斷增多，需要進行認知結構的再組織。因此，教師要從學生的認知特點出發，順應學生的思維，給予學生足夠的時間和空間，讓學生充分經歷觀察、分析、比較、驗證等數學探究過程，使學生的認知由模糊走向清晰，由膚淺走向深入，由片面走向全面，認知結構不斷趨向合理、豐滿、完善。

如教學蘇教版教材五年級“圓的認識”時，教師首先進行“你說我猜測”的游戲活動，出示長方形、平行四邊形和圓這三種圖形，要求描述時不能帶有名稱中的任何字詞，發展學生用語言描述圖形特征的能力。接著，創設“投球比賽”的情境，引導學生思考：為什么要圍成圓形隊伍？為什么把球筐放在中心位置才公平？這時，引領學生對正方形、長方形、圓進行對比，直觀得出將球筐放在圓形隊伍的中心位置，每個人到中心的距離都相等，這樣比賽才公平，然后在此基礎上，把研究的對象引向圓的本質特征——一中同長。最后，通過畫圓和折圓的活動，進一步探究圓心、半徑和直徑的相關知識。這個環節層層遞進，符合學生的認知特點，逐步引導學生組織合理的認知結構，由新知向舊知過渡，不斷加深學生的數學理解，使學生的數學思維品質不斷提升。

綜上所述，數學理解是動態的發展過程。在數學課堂教學中，教師應基于學生已有的認知水平和知識經驗，創設具有啟發性的問題情境，讓學生親歷知識的形成過程，順應學生的思維，促進學生的數學理解，發展學生的數學智慧。