基于EMD和ARMA模型的上證指數預測①

吳振宇 喻敏 金吉 姜楠

摘 要：針對上證指數具有非線性、非平穩性的特點，研究了一種基于經驗模態分解（EMD）和自回歸滑動平均模型（ARMA）的預測方法。首先利用EMD對上證指數數據進行平穩化處理，使上證指數數據更有規律性，改善上證指數數據的非線性、非平穩性特性，然后利用ARMA模型對分解后的數據建模預測。研究結果表明：和直接利用ARMA模型進行預測所得的結果相比，本文所提的方法預測精度更高。

關鍵詞：經驗模態分解（EMD） 自回歸滑動平均模型（ARMA） 上證指數 預測

中圖分類號：F832.51 文獻標識碼：A 文章編號：2096-0298（2018）06（a）-033-03

股市一直以來受諸多因素的影響，導致股市變化莫測，股票具有高風險、高回報的特點，有效的股市上證指數預測研究是降低風險，提高獲利的關鍵[1～2]。目前常用的股票預測研究方法包括：支持向量機法[3～4]、卡爾曼濾波法[5]、神經網絡方法[6～7]等。卡爾曼濾波法是將股票數據作為狀態變量建立狀態空間模型，該方法更加適用于對股票數據的在線預測，但難以估計噪聲的統計特性。支持向量機在處理小樣本方面有較大優勢，但一些參數的選擇將直接決定預測的精度，目前支持向量機仍然缺乏公認有效的參數選擇方法。神經網絡法具有較強的泛化能力，但神經網絡法容易在局部最小點出現錯誤，從而導致產生的預測結果不夠穩定。由于ARMA模型在建模時能將影響股票的因素綜合起來[8]，本文選取ARMA模型來預測上證指數，由于ARMA模型用于處理平穩序列，針對上證指數數據具有非線性、非平穩性的特點，需要先對其進行平穩化處理。對數據進行平穩化處理的方法主要有小波變換和經驗模態分解（EMD）方法。由于EMD在提取趨勢項上更有優勢[9]，因此本文選用EMD對上證指數數據進行平穩化。

針對上證指數數據非線性、非平穩性的特點，本文采用EMD和ARMA模型的組合方法來預測上證指數數據，本文選取網易財經自2014年3月26日至2016年11月26日期間的每日收盤價上證指數進行建模預測，首先利用EMD方法分解上證指數數據，獲得若干個分解的子序列，由于這些子序列能體現原始信號的不同尺度波動成分，因此使得分解后的數據比原始數據更加平穩，再用ARMA模型對每個子序列進行建模預測，最后將所有子序列的預測結果相加就得到了對原始上證指數數據的預測。

1 算法原理

1.1 EMD算法

經驗模態分解[10]（Empirical Mode Decomposition，EMD）方法的基本原理是將信號中不同特征尺度或趨勢逐級分解進而產生有限個固有模態函數（IMF），分解后的IMF分量體現了原始信號的不同尺度波動成分，因此EMD是一種有效的處理非線性信號的方法。其分解的具體過程為。

設待分解的信號為，對其進行EMD的具體步驟為：

（1）確定出信號的所有極大值和極小值。

其中，為隨機過程。

ARMA模型的定階也可以通過AIC準則來確定，其原理為：選取不同的p、q對時間序列進行擬合，計算出相應的AIC值。當AIC值達到最小值的模型就是最佳模型，AIC準則是衡量統計模型擬合優良性的一種標準，它可以用來權衡所估計模型的復雜度和此模型擬合數據的優良性。

2 實例分析與論證

2.1 股票數據采樣與處理

為驗證本文所提方法的有效性，選取網易財經2014年3月至2016年11月每隔一天測量的1000個收盤價上證指數進行建模預測。預測的基本過程為：利用經驗模態分解將原始時間序列分解為更加平穩的子序列，然后利用ARMA模型對每個子序列進行建模預測，得到各個模態分量的預測值，最后再將所有預測值加在一起，最終得到對上證指數的預測結果，其步驟如下。

（1）首先利用EMD方法將前900個原始數據分解成幾個不同特征尺度的IMF分量和余項。

（2）利用ARMA模型分別對前900個數據的IMF分量和余項進行建模。

（3）利用ARMA 模型對每個IMF分量和余項進行預測，再將所有預測結果相加，獲得對前900個股票數據的901～1000的股票數據的預測值。

（4）最后將獲得的901～1000的股票預測數據與原始數據901～1000的股票數據進行對比，評估預測誤差。

2.2 EMD分解結果

首先繪制原始收盤價上證指數曲線如圖1（a）所示，對收盤價上證指數的EMD分解效果如圖1（b）所示。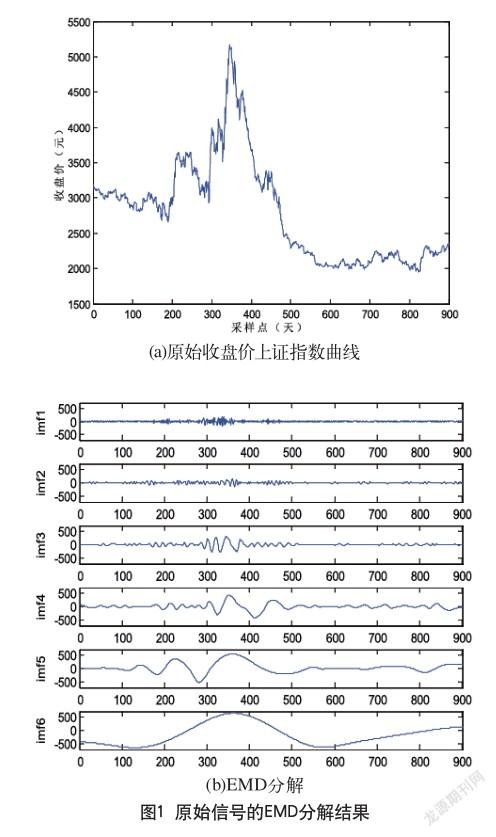

2.3 股票的預測結果

為了驗證本文所研究方法的有效性，分別對選取的股票數據利用ARMA模型和EMD-ARMA模型進行建模預測，并將其預測結果與實際股票數據進行對比，兩種預測模型的預測結果，如圖2中（a、b）所示。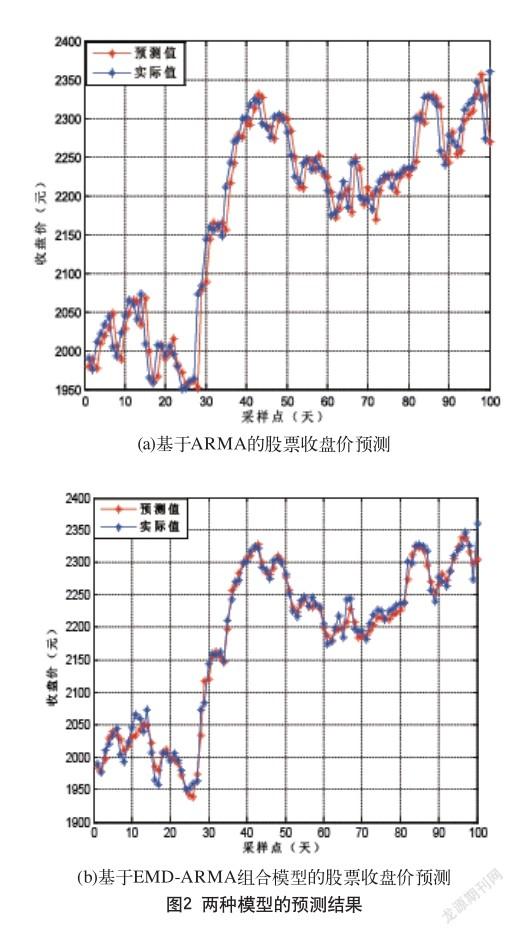

從圖2中可以看出，采用EMD-ARMA模型的預測效果要優于采用ARMA模型的預測效果，預測精度得到了顯著的提高，因為EMD能夠將原始股票數據分解為更加平穩的子序列，能更好地找出股票數據的內在規律，使得利用ARMA模型預測使能更好地跟蹤實際的股票預測數據。

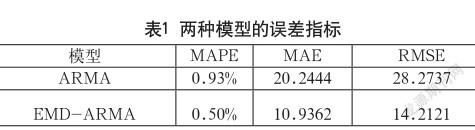
表1列出了兩種預測模型的誤差指標大小，本文采用平均絕對百分比誤差（MAPE）、 平均絕對誤差（MAE）和均方根誤差（RMSE）來衡量預測誤差，則預測誤差越小說明預測精度約好。從中可以看出，采用EMD-ARMA組合方法的誤差指標要明顯小于單獨采用ARMA模型的預測誤差指標，這同樣說明了EMD-ARMA模型能明顯提高股票的預測精度。

3 結語

本文研究了采用EMD-ARMA 組合的股票預測模型，得到以下結論：（1）EMD算法能將股票序列中不同特征尺度分解出來，使得分解后的數據更加平穩，規律性更強。（2）由于EMD對股票數據進行平穩化處理，極大地便利了利用ARMA模型對股票數據的建模預測過程，因此采用EMD-ARMA模型比ARMA模型的預測效果更好。

參考文獻

[1] 張晨希，張燕平，張迎春，等.基于支持向量機的股票預測[J].計算機技術與發展，2006，16（6）.

[2] 王玲.最優組合模型在證券市場預測中的應用研究[J].計算機仿真，2012，29（1）.

[3] 李強.基于支持向量機的股票預測研究[D].山東科技大學， 2013.

[4] 謝國強.基于支持向量回歸機的股票價格預測[J].計算機仿真， 2012（4）.

[5] 陳恩石.基于卡爾曼濾波及神經網絡算法對股價進行預測[M].

[6] 王愛平，陶嗣干，王占鳳.BP神經網絡在股票預測中的應用[J].微型機與應用，2010，29（6）.

[7] 鄭睿穎，伍應環.神經網絡在股票價格預測中的研究[J].計算機仿真，2011，28（10）.

[8] 孟坤，李麗.基于ARMA模型預測股票價格的實證分析[J].河北北方學院學報（自然科學版），2016，32（5）.

[9] 李慧浩，許寶杰，左云波，等.基于小波變換和EMD方法提取趨勢項對比研究[J].儀器儀表與分析監測，2013（3）.

[10] Chen H F，Zhao W X.New Method of Order Estimation for ARMA/ARMAX Processes [J].2010，48（6）.

①基金項目：國家自然科學基金項目（61671338）；國家級、省級大學生創新創業訓練計劃項目（20160488048）。

作者簡介：吳振宇（1982-），男，漢族，河南洛陽人，碩士研究生，主要從事股票預測分析方面的研究。