關注三角知識的解題功能

黃旭明

(福建省福安市第三中學 355002)

在三角函數的學習中，常常把學習的重心放在三角函數的圖象性質與三角公式的變形技巧上，而忽略了三角知識的應用價值.實際上，如果在解題中能恰當地引入三角知識，可化繁為簡，化難為易，優化解題，突顯三角知識的解題功能.本文分類舉例介紹三角知識在諸多問題中的廣泛應用.

一、求解最值問題

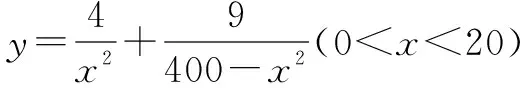
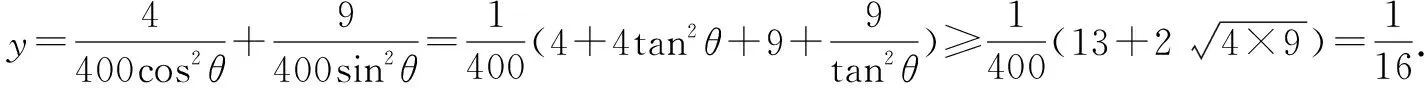
二、求解取值范圍問題

例2 若2x2-2xy+y2=1,則x+2y的取值范圍是( ).

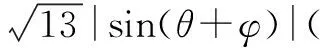
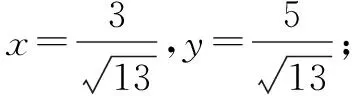
三、求解不等式問題

例3 已知|x|≤1,求證(1-x)n+(1+x)n≤2n(n∈N*).

證明由條件|x|≤1,可設x=cosx(0≤α≤π),則

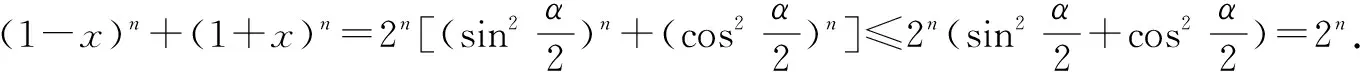
四、求解數列問題

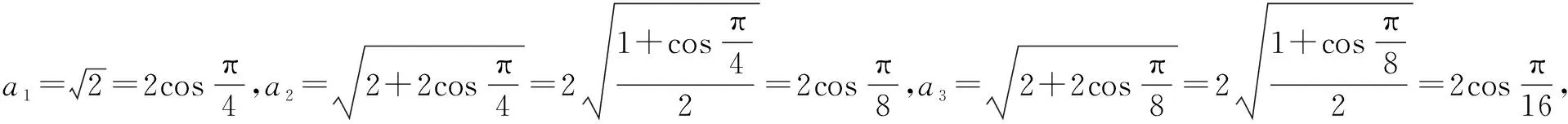
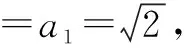
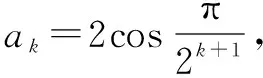
五、求解向量問題

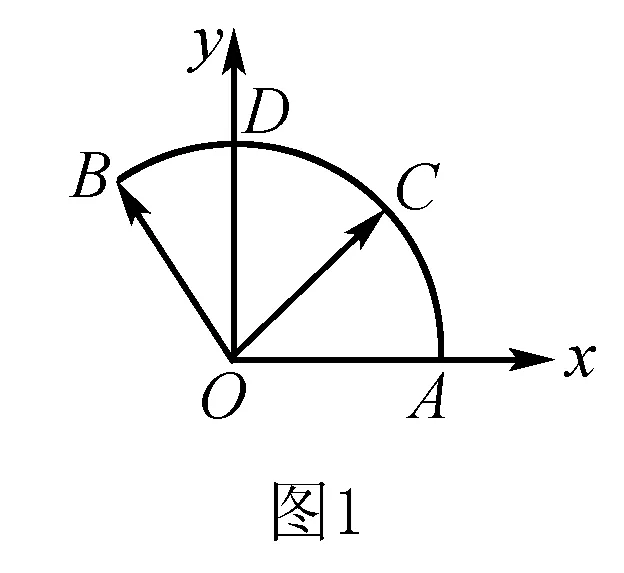
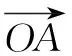
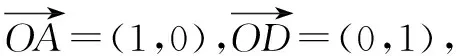
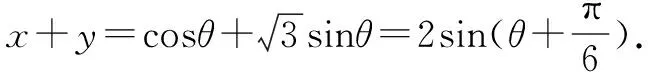
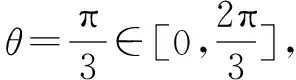
六、求解平面幾何問題

例6 如圖2，是三個并排的相同正方形，求角α+β的大小.

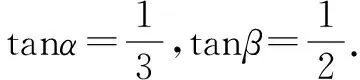
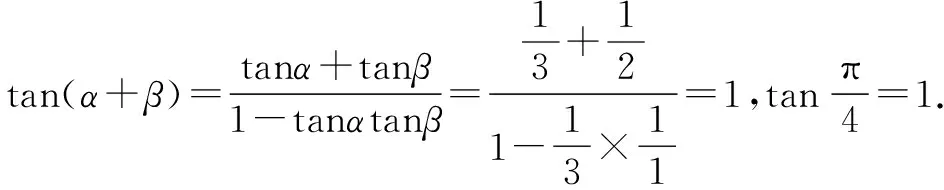
七、求解解析幾何問題

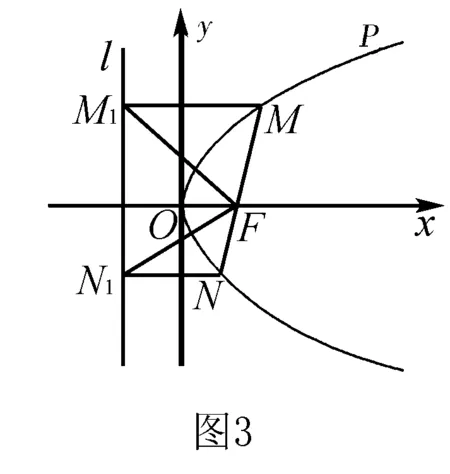
例7 如圖3，過拋物線y2=2px(p>0)的焦點F的直線與拋物線相交于M、N兩點，自M、N向準線l作垂線，垂足分別為M1、N2.

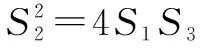
解(1)記l與x軸的交點為F1.由拋物線定義知FM=MM1,FN=NN1,又MM1∥FF1∥NN1,故∠MFM1=∠MM1F=∠M1FF1,∠NFN1=∠NN1F=∠N1FF1.

所以∠M1FF1+∠N1FF1=∠MFM1+∠NFN1,得∠MFN1=90°，所以FM1⊥FN1.

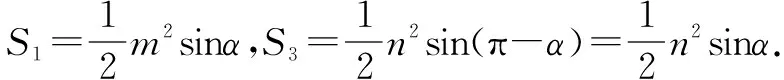
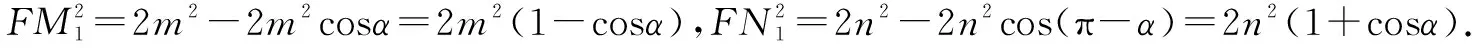
從以上諸例可以看到，三角的知識和方法可運用到各種類型的題目中，而且可以化隱為顯，化難為易，從而應用熟知的三角方法順利實現解題.實際上，各章節的數學知識都有廣泛的應用，注意挖掘出各種數學知識方法的工具作用，對培養數學意識，增強解題能力，提升數學素養，具有重要意義.