縱橫聯系 引申拓展
——對一道圓錐曲線題的探究

浙江省金華市第六中學 (321000)

虞 懿

(Ⅰ)求橢圓C的標準方程；

最近，筆者在研究此題時，發現此題可以引申、推廣得到圓錐曲線的幾個美妙結論．

一、縱向拓展

由上述試題得到啟發，筆者認為在橢圓焦點所在直線上可能存在一定點，它與焦點弦端點所張的向量點積為定值，并將橢圓一般化，則可得：

證明：設直線AB方程為x=my+c,點A(x1,y1),B(x2,y2),Q(t,0).

(a2+b2m2)y2+2b2cmy-b4=0.

二、逆、雙向拓展

荷蘭數學教育家費賴登塔爾指出：反思是數學思維活動的核心和動力．在反思上述結論證明的可逆性過程中，筆者展開了對其逆命題真假性的探究．

綜合結論1、2，可得：

三、橫向拓展

波利亞說：“類比是偉大的引路人．”對于橢圓我們有結論3，那么對于雙曲線是否也有同樣的結論呢？回答是肯定的，證明與橢圓結論3的基本相同，只需將橢圓結論證明過程中的b2換成-b2即可，相關結論如下：

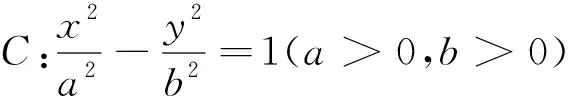
同樣的，對于拋物線也具有上述類似結論成立．

四、進一步拓展

掩卷沉思，若將過焦點F的直線改為過x軸上定點P的直線，對于圓錐曲線是否還具有類似的定值定點結論？回答是肯定的．

(結論6、7、8仿上證明即可)

后記：探究試題是高中數學教師的一項重要工作，也是教師的一項基本功．通過對本道優質試題的深入思考，不僅能深刻地理解圓錐曲線是真正統一的家族，感受數學的和諧統一美，更能在不斷反思追問中潛移默化地進步，思考更加地深刻，自然就能體會到“采菊東籬下，悠然見南山”的意境！