運用相關思維對一道中考壓軸題的教學觀察

☉湖南省常德芷蘭實驗學校初中部 陳金紅

一年一度的中考數學壓軸題，既是命題者頭痛的“磨難”命制，更是考生心有余悸的“傷痛”.如何在緊張的考場有效輕松應對，研究中考壓軸題就是一件必不可少的實踐活動，為此我們對湖南省常德市2018年的數學壓軸題第26題做教學剖析，希望我們的教學觀察能為同仁帶來一點黎明曙光：

題目 已知正方形ABCD中，AC與BD交于O點，點M在線段BD上，作直線AM交直線DC于E，過D作DH⊥AE于H，設直線DH交AC于N.

（1）如圖1，當M在線段BO上時，求證：MO=NO；

（2）如圖2，當M在線段OD上時，連接NE，當EN∥BD時，求證：BM=AB；

（3）如圖3，當M在線段OD上時，連接NE，當NE⊥EC時，求證：AN2=NC·AC.

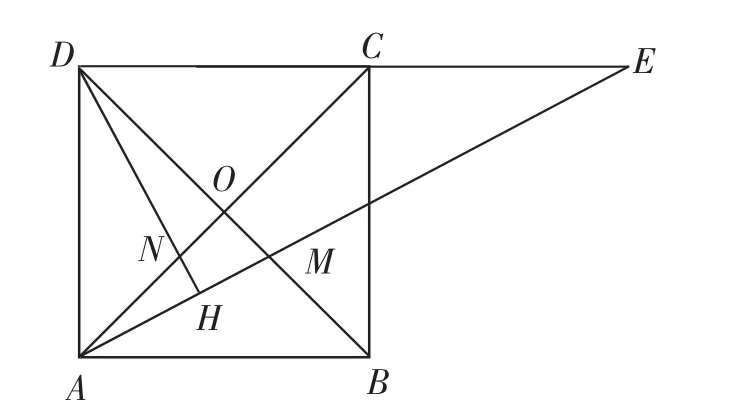
圖1

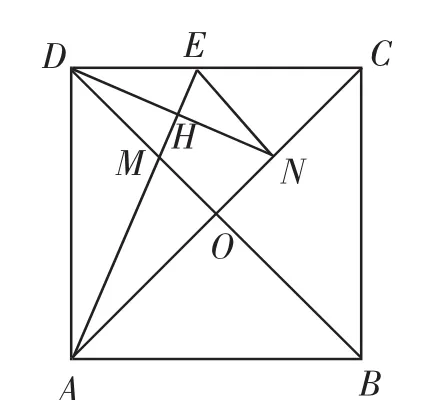
圖2

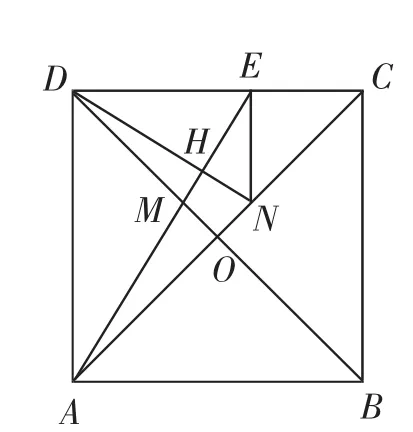
圖3

一、涉及考點

（1）特殊圖形：正方形、等腰三角形、直角三角形等；

（2）幾何性質：正方形的性質、直角三角形的性質、相似三角形的性質與判定、全等三角形的性質與判定、線段垂直平分線定理等；

（3）可以運用的選學內容：四點共圓、圓冪定理、射影定理等.

二、基本解析

三個小問題的提出是基于點M在正方形對角線BD被對角線交點平分線段的不同位置所引起，其實隱喻“動點M”乃問題之間的思維聯系紐帶！

第（1）問主旨是考查兩個直角三角形的全等的運用，條件一是有一對相等的直角、條件二是一對相等的銳角（由同角（或等角）的余角相等得出的）、條件三是一條直角邊相等（由正方形對角線相等互相平分性質得到的）；具體判定方法是“ASA”或“AAS”推出：△OAM △ODN，從而有MO=NO.

第（2）問，當點M運動到OD上時，同理仍有△OAM△ODN，從而仍有MO=NO.由此可得到許多相等的線段，比如EM=NC、BM=AN等.

同樣也有許多的全等三角形，比如△ADM△DCN、△BAM △ADN等.還有許多的相似三角形，比如不連線時的△DME △BMA，△CEN △CDO，Rt△HDE、Rt△HAD與Rt△DAE三個三角形也相似（直角三角形重要性質——射影定理），若連輔助線MN有△OMN△ODC等；見圖4.綜合上面的信息平行四邊形MNED；又已知DH⊥AE于HN，即AH是DN的垂直平分線?AN=AD.而AB=AD，BM=AN，于是有AB=BM.繼續演繹下去會有更多的全等三角形和相等的角和線段（略）.

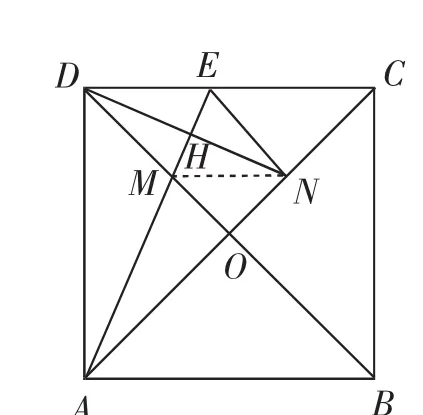
圖4

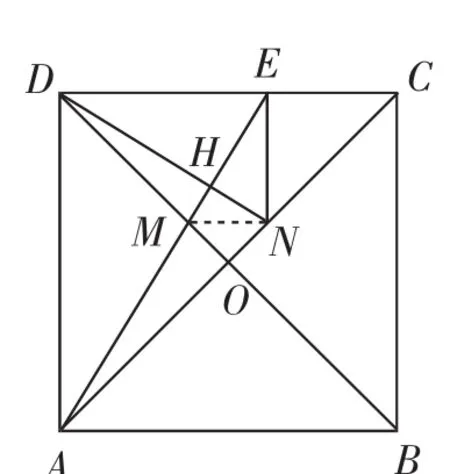
圖5

三、教學觀察

⒈題目設計：蘊藏思維定式與圈套障礙點

對于第（1）問，屬于基本常規給分點，很容易上手，乃激發答題者的興趣和解題斗志的設計；

對于第（2）問，考生很容易糾纏于想通過證明∠BAM=∠BMA去證明線段AB=BM，其實是一個死胡同！顯然跳出這個設計的“定式思維”最明智的方法是像上面的分析一樣發散開來！

對于第（3）問，若從NE⊥EC、AD⊥DC?EN∥AD出再推理演繹的話也會出現死胡同！或利用直角三角形射影定理模型法展開推理仍會出現死胡同！跳出這個設計的“思維”圈套最明智的方法也就是上面說的信息發散！

2.題目檢測：考生數學思維的長度與解題能力

顯然要一氣呵成解決這些問題，從顯性的圖形與已知出發，先做基本的演繹推理得出隱形的一些相等的角、相等的線段、全等的三角形、相似的三角形，再兩兩組合得出新的相等的角、相等的線段、全等的三角形、相似三角形，即發散更多的隱形的數量、位置和變換關系.這些無不體現出考查知識的覆蓋度、思維的連貫性和邏輯的嚴謹性！

3.解題方法：亦可合情推理，拼湊法樸素輕松

顯然嚴格推理不是一件在規定時間內輕松解決的事情，咋辦？根據新的課程標準和數學學科核心素養的基本要求，不妨合情推理展開思維：直接計算推理，即：

①等腰Rt△NEC中，NC2=2NE2；②Rt△NED中，NE⊥DE、EH⊥DN于H?NE2=NH·ND（射影定理）.聯合知NC2=2NH·ND.

③∠DHA=∠DOA=90°?四點D、H、O、A共圓?NH·ND=NO·NA.

4.思維模式：暗含提綱挈領的紐帶

顯然生活中一個事件常常引發多個相關事情的發生（多米諾骨牌效應），映射到數學命題中來，利用幾何變換如一個點的運動，與定點相關聯得到一個圖形如線段就會是動線段，產生“子母”聯動形象，于是相關思維的有機破解能力就自然被要求了！本題的一個動點就是正方形ABCD的對角線BD上的點M，與定點A相連的線段AM就是動線段，于是相關聯的其他圖形就受其制約了，于是“動點M”乃問題之間被“提綱挈領”的思維聯系紐帶！這正是我們研究中考壓軸題教學觀察的結論：找到“相關思維”被“綱舉目張”的思維動點，為我們的解題指明前進的方向！