找尋“巧合”中的規律
——2018年南京市中考第27題感悟

☉江蘇省南京市致遠初級中學 何君青

☉江蘇省南京市致遠初級中學 張田田

2018年中考塵埃落定，各地中考試卷相繼出爐，南京市中考試卷新穎、獨特，歷來受到全國各地教育同行的關注.今年南京市中考試卷依然保持一貫的作風，知識覆蓋廣，區分度適宜.試卷第27題看似簡單，卻內涵豐富，從求直角三角形的面積入手，繼而推廣到一般三角形的面積求法，考查可謂獨具匠心，看似“巧合”，實則蘊含著規律.筆者對此題進行了深入研究，感悟頗深，故撰文與同行交流.

一、原題呈現

下框中是小穎對一道題目的解答.

題目：如圖1，Rt△ABC的內切圓與斜邊AB相切于點D，AD=3，BD=4，求△ABC的面積.解：設△ABC的內切圓分別與AC、BC相切于點E、F.CE的長為x.根據切線長定理，得AE=AD=3，BF=BD=4，CF=CE=x.根據勾股定理，得（x＋3）2＋（x＋4）2=（3＋4）2.整理，得x2＋7x=12.所以S△ABC=1 2AC·BC=1 A D 2（x＋3）（x＋4）=1 E O 2（x2＋7x＋12）=1 C F B圖1 2 ×（12＋12）=12.

小穎發現12恰好就是3×4，即△ABC的面積等于AD與BD的積.這僅僅是巧合嗎？

請你幫她完成下面的探索.

已知：△ABC的內切圓與AB相切于點D，AD=m，BD=n.

可以一般化嗎？

（1）若∠C=90°，求證：△ABC的面積等于mn.

倒過來思考呢？

（2）若AC·BC=2mn，求證∠C=90°.

改變一下條件：

（3）若∠C=60°，用m、n表示△ABC的面積.

分析：本題是三角形、圓的相關知識與思想方法的綜合運用，是蘇科版教材九年級（上）“切線長定理”的延伸，在教學時，教師會利用此圖研究直角三角形的內切圓的相關結論并探索勾股定理.本題有3小問，第（1）問“正著做”，第（2）問“反過來做”，第（3）問“一般化做”，環環相扣，難度逐步上升，題目不僅注重知識之間的連貫性、幾何語言的規范性，更注重對學生發散性思維的培養.本題源于教材、高于教材，以文字、表格、圖形等方式多樣化呈現，有利于學生讀懂題、理解題意.從考查內容上看，本題從求直角三角形的面積入手，運用切線長定理、勾股定理解決問題，這些都是中考中的核心考點，注重對基礎知識、基本技能的考查，同時注重對基本活動經驗、類比思想、逆向思維的考查；從考查方式上看，本題打破以往的考查方式，給予學生適當的解題方法指導，降低了難度，讓學生對壓軸題的恐懼感大大降低；從考查意義上看，本題的考查注重知識間的連貫性，一正一反地解決問題，讓學生對知識的理解更加深刻，也提醒教師在后續授課時需注重知識發生、發展、探究的過程，讓學生學到知識，理解知識，會運用知識解決問題.所以，無論從試題基礎性、新穎性、公平性、自洽性看，還是從試題的信度、效度、區分度、可推廣性看，本題都是一道不可多得的好題.

二、解法剖析

本題的第（1）問和第（2）問做法比較常規，難度不大.第（3）問要求學生要有轉化的思想，化斜為直，從而解決問題.第（3）問解法如下.

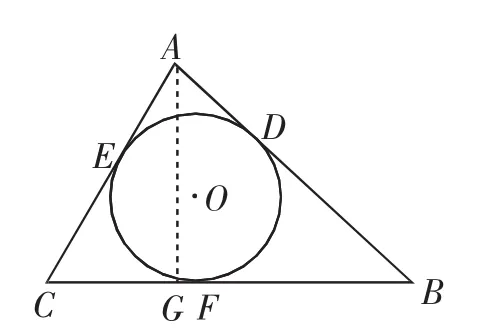
圖2

分析：此法先作出三角形的高，再利用三角函數和勾股定理，求出三角形的面積.從解題教學的角度看，此方法從已知到可知，從要知到需知，擬定可行的步驟成功地解決了問題.此法“源”于學生對方框中方法指導的理解，體現了知識間的連續性.這種解題的步驟源于教師在日常教學中的點滴，要給予學生探索的時間和空間，使學生對數學概念的形成產生痕跡.在上課時，教師需要充分讓學生對數學結論發表自己的看法，給予足夠的探究時間，學生的數學能力必然會有大幅度的提升.

三、推廣研究

為了能將本題研究得更加透徹，從“巧合”中探索出規律，筆者又設計了如下幾個問題.

拓展題1：若∠C=45°，用m、n表示△ABC的面積.

解：如圖3，過點A作AG⊥BC，垂足為G.

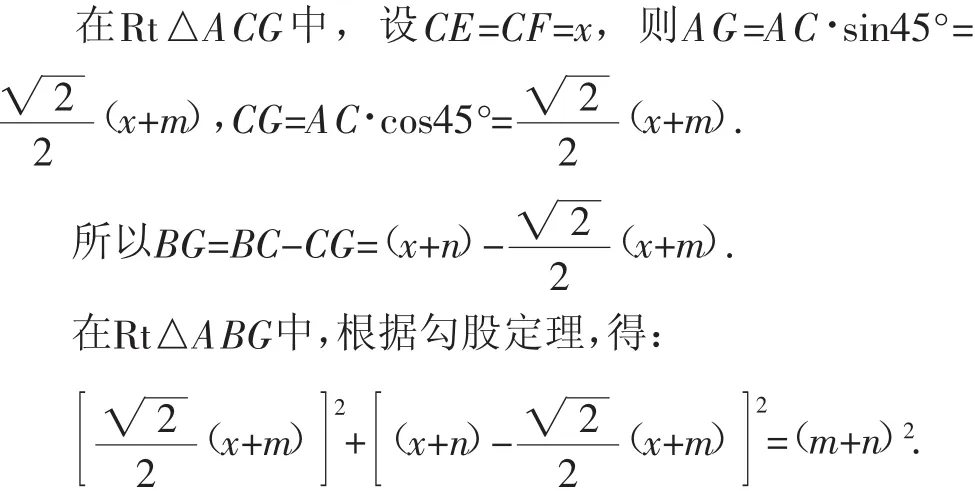
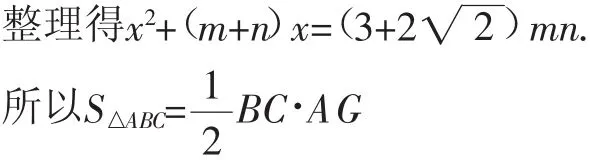
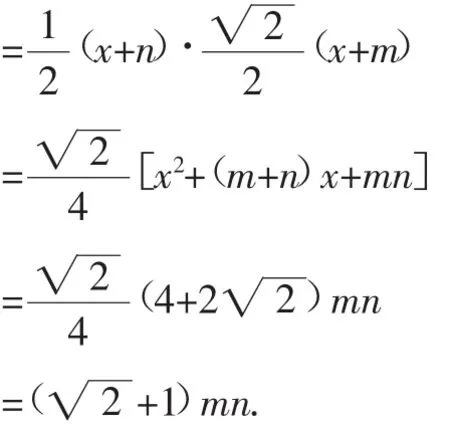
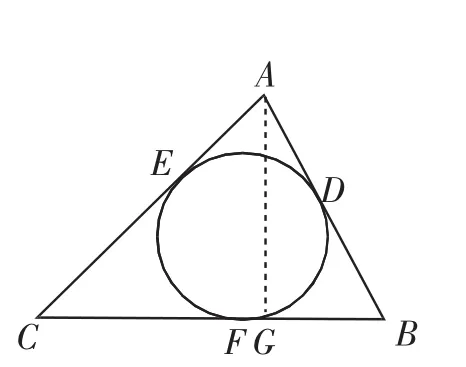
圖3

拓展題2：若∠C=α（0°＜α＜90°），用α、m、n表示△ABC的面積.

解：如圖4，過點A作AG⊥BC，垂足為G.

在Rt△ACG中，設CE=CF=x，則AG=AC·sinα=（x+m）·sinα，CG=AC·cosα=（x+m）cosα.

所以BG=BC-CG=（x+n）-（x+m）cosα.

在Rt△ABG中，根據勾股定理，得：

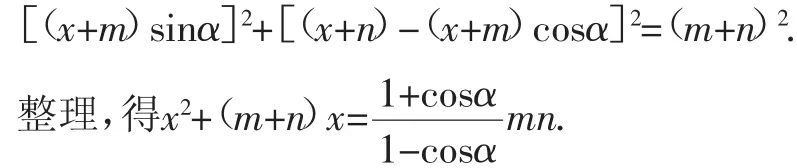
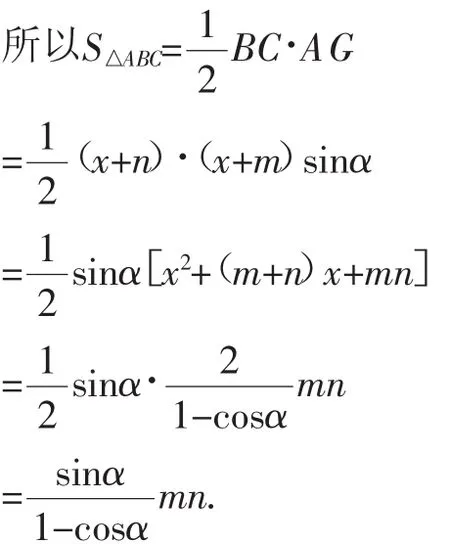
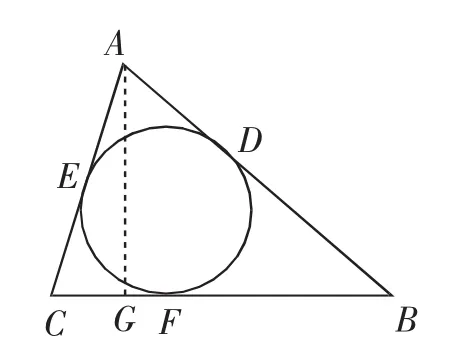
圖4

分析：拓展題1將考題中∠C的度數從60°變成45°，方法一致，難度基本相當，區別在于答案中含有根號，計算量比考題有所增加.拓展題2將考題中∠C的度數變得更為一般，用α（0°＜α＜90°）進行了表示，在表達各邊時需要用三角函數表達，雖然方法一致，但難度大大增加了.

荷蘭數學家弗萊登塔爾提出：學習數學唯一正確的方法是實行“再創造”，也就是由學生本人把要學的東西自己發現或創造出來.故此題在平時教學時需進一步拓展，找尋規律，這樣才能讓學生真正“會學”，在課堂上實現知識的創新、整合，自主探索、合作交流，根據已有的體驗，用自己的思維方式重新創造，得到更多的收獲.

四、感悟思考

考試，無論是期中、期末還是中考，都十分注重對基礎知識、基本技能、基本思想方法和基本活動經驗的考查.對于學習數學，基礎是根本的前提，若沒有基礎，能力的培養和提高則無從談起.故在教學的過程中，教師不僅要教學手段多樣化，更要注重解題方法的多樣化，注重通過題組的教學，探尋其中蘊含的數學規律.本題從求三角形面積這一核心考點出發，繼而變形、推廣，不僅關注數學閱讀能力，以及基礎知識、基本技能，更讓教師在后續的教學中關注學生數學經驗的獲得，重視基本活動經驗的積累，由此可見這道中考題的用心良苦.

1.有利于提高學生的能力

隨著學校招生的需要，“功利性”愈演愈烈，應試教育成為很多學校的主要教學方針，凡是中考必考的核心考點就會進行大量的反復訓練，中考不考的知識大膽舍棄，不在課堂上提及.這種不良的教學模式對學生能力的培養和后續的發展大有壞處.本題恰好是對這種不良的教學模式的極大沖擊，平時的“題海戰術”對這類題毫無作用，在題海中“遨游”的學子對于這種題目的解決不占任何優勢，反而平時課堂注重知識的形成、發展，喜歡探究的學生占一定的優勢，這符合新課標的要求“引發學生的數學思考，鼓勵學生的創造性思維的培養”.

在做題時，建議學生多去探索問題中蘊含的數學規律，不要只埋頭做題，思考問題時，多經歷觀察、猜想、分析、綜合、歸納和論證等活動，親身體驗知識的發生、形成與發展過程，學會研究的策略和方法，發展探究和歸納的能力，獲得終身受益的數學素養.

2.有利于促進教師的發展

中考對后續的教學應起到一定的導向作用，教師在平時教學中應多關注學生能力的培養，致力于教材資源的開發，充分研究命題的規律，注重解題時的一題多解，一題多變.

教師在教學時，要多給學生探索的時間和空間，從題出發，探索題目背后的價值，讓一個問題變成一類問題，從而讓學生解一題、會一類、通一片.這樣的做法也能培養學生主動探究的能力，增強學習數學的興趣.當學生對數學產生濃厚的學習興趣時，自然有強烈的求知欲，教學效果更會事半功倍.

一道中考題，看似簡單，卻又不“簡單”，題目看似“巧合”，實則蘊含豐富的規律，讓教師明白活用好題、給予學生足夠空間和時間的重要性，讓學生了解自主探究、領悟數學內涵的學習要義.