基于提升學生核心素養的初中函數有效教學設計研究

（蘇州工業園區金雞湖學校 江蘇蘇州 215021）

初中函數在數學課程中的地位非常重要，函數是描述運動、變化的基本概念，數學中許多概念或由函數派生；或由函數統率；或可歸之為函數觀點研究。基于提升學生的核心素養，函數教學中不僅要重視學生的解題能力，還需培養學生學習興趣與自主學習能力，創建真實的教學情境，培養初中生的抽象建模能力，以此形成良好的教學模式，達到預期的工作目的。

一、使用問題情境培養學生抽象建模能力

教師可以為學生創設問題情境，向學生提出問題，引導學生針對問題進行思考與交流，最終可以自主解決問題，以便于提升學生的抽象建模能力。例如：教師在新授“函數”概念時，可先為學生創設多組與實際生活相互關聯的教學情境，通過問題組的研究，先理解變量與常量的概念。對于“函數”的定義，教師可讓學生之間進行小組交流，并提出問題要求：學生需要使用數學語言，并根據之前的學習經驗，進行歸納與總結。學生理解了各個問題中的自變量與因變量的關系，體會變量之間的相互依存關系和變化規律，在此基礎上進行歸納、抽象、總結，便能得出函數的概念。如果學生不能更好的對抽象的函數進行定義，那么就要結合學生的學習條件創設問題的分析活動，以便于培養學生在函數問題方面的分析與解決能力[1]。再比如：在二次函數的教學中，課堂上一開始播放用炮彈轟炸的新聞畫面，然后用Flash動畫模擬炮彈從發射到落地的整個過程，讓學生觀察炮彈的運行軌跡（拋物線），炮彈飛行的最高點（頂點）、發射點到落地點的距離等。接著告訴同學，這是一個物理問題，這些問題都能用二次函數的知識得以充分解決。當學生認識到學習的內容有如此大的作用時，就會極大地激發他們的學習興趣和求知欲，喚醒學生的注意。在學生學習期間，要求學生使用建模思想進行總結，教師需及時發現學生在學習與理解方面的問題，采取科學的措施解決問題，并進行教學糾正。

二、利用探索活動培養學生推理想象能力

函數是初中數學的核心概念，可用“學函數，用圖像”的觀點指導學生函數學習：從概念層面上看，豐富表征，完善結構，便于概念抽象；從思想方法層面看，以形助數、數形溝通，實現數形結合；從心理學角度看，用圖思考，形象直觀，有助于建立信心。具體表現在：（1）用圖像，從“形”的角度刻畫和理解函數及其相關概念；（2）用圖像，為函數性質的發現、描述、理解和記憶提供方法；（3）用圖像，從變換的視角將復雜函數看“簡單”；（4）用圖像，架起方程、不等式通往函數的“橋梁”；（5）用圖像，構建直觀模型使函數問題不抽象。例如：在講授一元一次方程、二元一次方程（組）、一元一次不等式與一次函數的內在聯系時可給出例題：畫出函數y=-2x+3的圖象，結合圖象求：（1）方程-2x+3=0的解；（2）不等式-2x+3＜0的解集；（3）不等式組-3≤-2x+3≤7的解集。在學生探究的時候，很可能會出現表面化的交流問題，教師需引導學生之間形成深層次的交流模式，并在積極探索中總結豐富經驗，積極參與到各方面的學習活動中，以此提升學生的整體學習效率與質量，滿足當前的教學要求。解析：任取直線y=-2x+3上兩個點的坐標，如選取（0，3），（1.5，0），繪出圖象如（圖1）

圖1

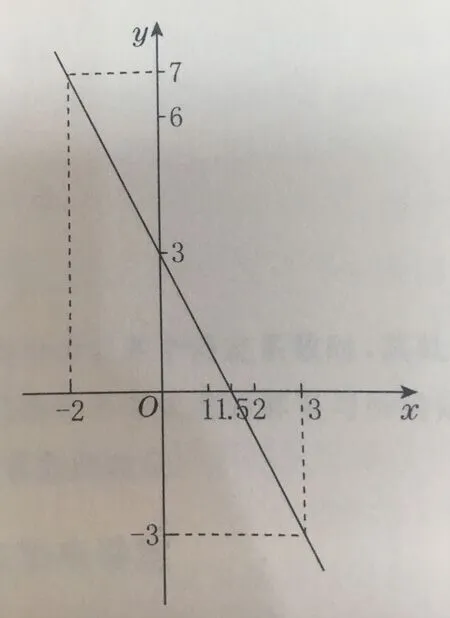
圖2

（1）根據一次函數與一元一次方程的關系，直線y=-2x+3與x軸的交點的橫坐標即為方程-2x+3=0的解，于是，從圖象上看，方程的解為x=1.5；（2）根據一次函數與一元一次不等式的關系，知直線y=-2x+3在x軸軸下方的部分對應的x的值，就是不等式-2x+3＜0的解集，顯然，-2x+3＜0的解集為x＞1.5；（3）由（2）中的解題經驗，如（圖2），我們在直線上找出點（-2，7），（3，-3），可以發現，不等式組-3≤-2x+3≤7的解集應該就是一次函數y=-2x+3的函數值在-3到7之間（包括-3和7）對應的自變量范圍：-2≤x≤3。上面的求解過程充分體現了數形結合思想。本質上說，也是對一次函數圖象與一元一次方程、一元一次不等式（組）之間“數”與“形”聯系的一種深刻認識，需要同學們認真體會和感悟。教師在講解知識的時候，還需創建現代化的教育機制與模式，提供學生進行探究性學習的題材，重視對學生綜合應用知識能力的培養，提升整體探究教學活動的應用水平[2]。

三、運用基本性質培養學生運算與數據分析能力

教師在函數教學中需培養學生的運算與數據分析能力，引導學生更好的理解函數定義與圖像性質，并在科學教學中，創設現代化的教育模式。例如：在講授反比例函數性質時，可以給出例題：直線y=ax（a＞0）與雙曲線交于A（x1， y1）、B（x2，y2）兩點，則4x1y2-3x2y1=____。在教師提出問題之后，可以要求學生進行運算，并針對數據進行科學合理的分析，確保學生在學習中更好的理解與掌握知識。這道題如果聯立方程組，用含a的代數式表示兩組解（即A、B點的坐標），再求值，必然會耗費很多時間，而且對于方程組的求解、運算能力都提出了很高的要求，這顯然不是我們要追求的解決方法。認真分析本題，繪出草圖，會發現直線、雙曲線在坐標系下的兩個交點是關于原點成中心對稱的，這個發現帶來的信息就是A、B兩點的橫坐標與縱坐標分別互為相反數，即x1=-x2，y1=-y2。于是，4x1y2-3x2y1=4x1(-y1)-3(-x1)y1=-x1y1，由于點A（x1，y1）在雙曲線上，所以，即-x1y1=-3。通過反比例函數中心對稱的性質使問題得以簡化，這是數形結合求解策略的典型應用，培養學生運算與數據分析能力。再比如，由于選擇題型特點，可利用猜測、合情推理、估算獲得正確答案，這樣往往可以減少運算量，可以加強思維的層次。如（圖3），已知知雙曲線經過直角三角形OAB斜邊OA的中點D，且與直角邊AB相交于點C。若點A的坐標為（-6，4），則△AOC的面積為（ ）A.12 B.9 C.6 D.4。由于點A的坐標為（-6，4），所以△AOB的面積為12，又點D是OA的中點，可推斷AC＞BC，所以△AOC的面積超過12的一半，故選B。估算法，省去了很多推導過程和比較復雜的運算，可以節省寶貴的時間，從而提高解題速度。為了更好的培養學生運算與數據分析能力，教師還可以使用“單回路、雙回路”的方式進行教學，并創建現代化與先進性的教育機制，確保在新時期發展的背景之下，全面提升整體教學工作效率與質量，滿足當前的發展需求。

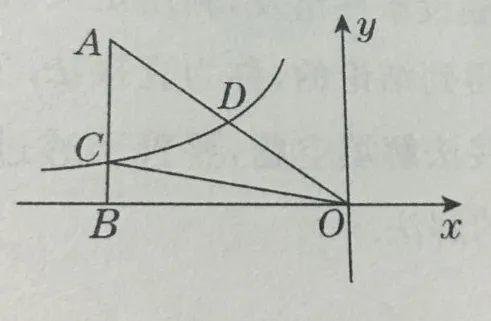
圖3

四、采用歷史文化培養學生人文與審美能力

教師還需重點培養人文與審美能力，滿足核心素養的教育要求。對于人文與審美能力而言，是學生在日常學習中漸漸形成的能力，教師可根據學生的學習特點與年齡特點，創設帶有人文精神與數學文化的函數教學課堂氛圍，重點關注學生數學價值、情感與審美教育工作，使用合理的教學方式培養學生學習能力，陶冶情操。例如：函數概念講解時，不妨可給學生介紹函數概念的發展史，再將其與如今的函數定義聯系起來分析，學生能更好地理解函數的概念。因為有生動的歷史背景做鋪墊，抽象的概念變得“有血有肉”，易于接受。再比如，如（圖4），在已知拋物線y=ax2+bx+c（a≠0）的對稱軸為直線x=1，且拋物線經過A（-1，0）、C（0，-3）兩點，與x軸交于另一點B。當求出這條拋物線所對應的函數關系式后，要在拋物線的對稱軸x=1上求一點M，使點M到點A的距離與到點C的距離之和最小，并求此時點M的坐標。可先介紹著名的“將軍飲馬”故事，熟悉這個“將軍飲馬”的最值模式，即可明確點M所在位置為BC與直線x=1的交點。在主動思考的情況下，更好的理解函數背景知識與對生活的影響，在學生合理學習的過程中，全面提升整體函數教學工作水平，以便于培養學生的學習能力，創建現代化的教育機制，達到預期的工作目的。

五、應用多媒體手段培養學生學習興趣與自主學習能力

教師在培養學生學習興趣與自主學習能力期間，教師還需利用科學方式創設教學氛圍。一方面，教師可以使用多媒體教學工具，為學生講解關于函數圖像的知識，使得學生更好的理解抽象知識與內容，并增強整體教學工作效果，激發學生的學習興趣。比如一次函數、二次函數、反比例函數的圖像及其圖像變換是重點內容，關于函數圖像的傳統畫法，是通過師生列表、描點、連線而得，畫出的是靜止孤立、間斷的點和線。教師可以讓學生在交互的動態的網絡環境下學習，函數值隨自變量的變化而同步變化以及對應運動的軌跡，從而得到完整精確的函數圖像，充分掌握函數的性質和抓住圖像的平移、旋轉、軸對稱圖形變換特征。另一方面，教師可以要求學生在網絡中自主搜索有關函數知識，并進行自主學習，若有疑問或好的見解，可以通過網絡進行遠程交流互動。通過多媒體，交互反饋，有利于提升學生的學習水平。

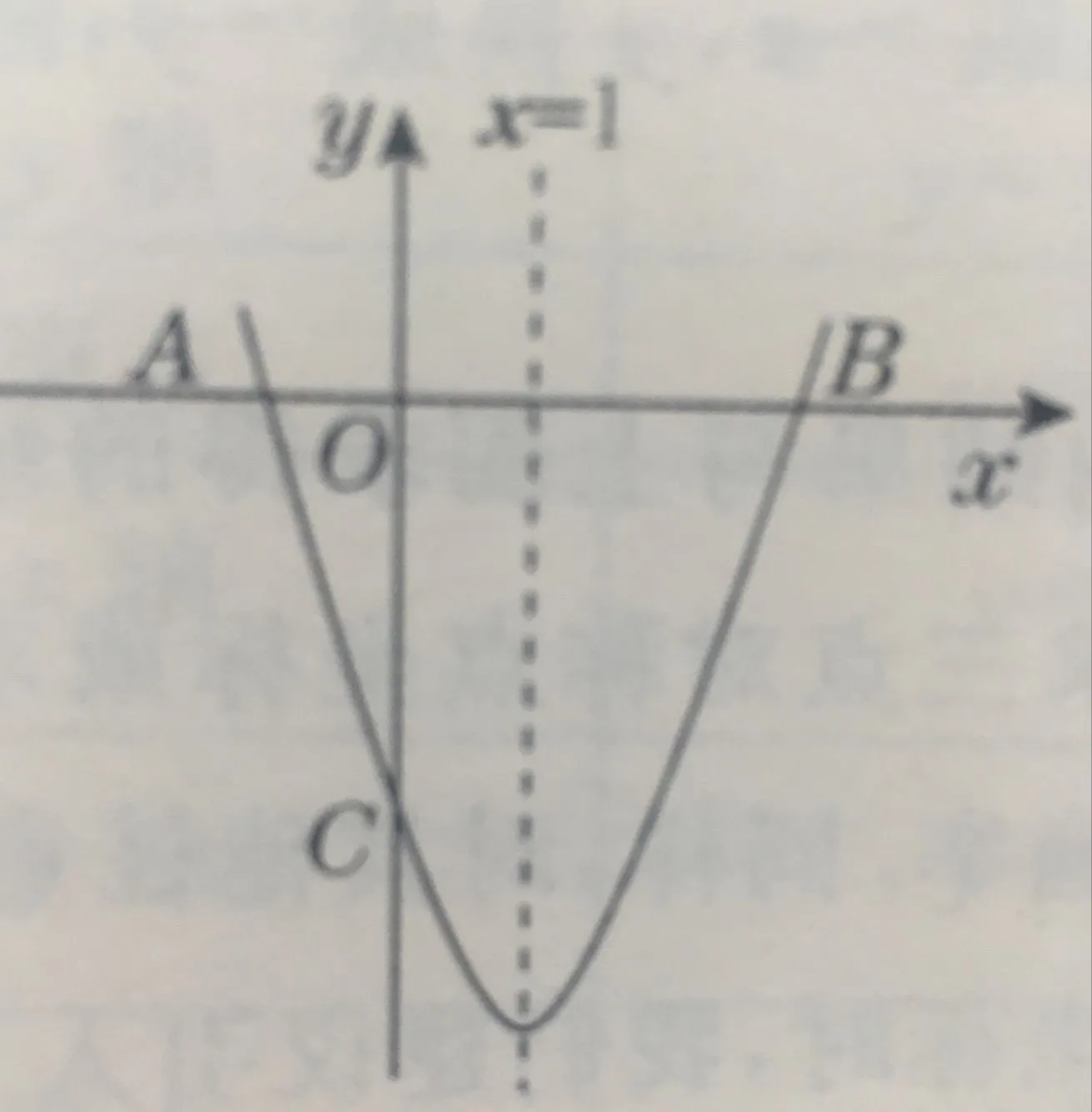
圖4

結語

函數教學是一個系統工程，基于全面提升學生的核心素養，需要運用運動聯系的觀點整體設計，制定完善的教學方案。概念教學前要通過先學知識提供先行組織材料，作好必要的鋪墊，“降低學生學習的起點”；教學中應揭示函數概念的本質屬性，借助具體的函數教會學生基本函數的圖象和性質，同時讓學生掌握一套研究函數的策略；教學后，宜加強函數知識的遷移與運用，幫助學生樹立函數運用意識與觀念，強化函數與其它知識的有機整合，切實提高學生對函數觀念的理解，同時為后續學習作好必要的準備。在新時期發展背景之下，總結豐富的教育經驗，利用科學合理的方式完成當前核心素養教育任務。