基于不對稱帶寬的路徑信號協調控制模型

姚 佼，高傲翔，王 飛，謝 明，謝祥俊

YAO Jiao1,GAO Aoxiang1,WANG Fei1,XIE Ming2,XIE Xiangjun2

（1.上海理工大學 管理學院，上海 200093；2.江蘇高科物流科技股份有限公司，江蘇 南通 226156）

(1.Management School,University of Shanghai for Science and Technology,Shanghai 200093,China;2.Jiangsu Gaoko Logistics Technology Co.,Ltd,Nantong 226156,China)

0 引言

城市道路交通通勤OD中出行者的路徑并非直線型的干線線路，實際中存在大量的轉向、掉頭等非直線型路徑，相關的研究表明，交叉口的轉向車流占50%以上[1]。另一方面現狀的城市道路協調控制研究主要集中在城市道路干線協調控制，其控制的目標主要分為綠波帶寬最大化和干線總延誤時間最小兩類。基于延誤時間的模型由于其復雜性和高度非線性，通常很難求解[2]；高峰時期，最大化通過能力成為城市道路交叉口信號協調控制的主要目標，此時綠波帶寬最大化的模型具有較好的實用性，對于城市交通效率和通行能力的提升效果顯著。

對于傳統的干線信號協調控制，國內外專家學者對此進行了深入的研究。Little等人首先提出最大帶寬混合整數線性規劃MAXBAND模型[3]；Gartner等人提出一種多帶寬干線協調控制模型MULTIBAND模型，該方法在MAXBAND模型的基礎上改進，它可以根據上下行交通量不同給出多種協調綠波帶寬，與MAXBAND模型相比較該模型更符合實際道路條件[4]；此后，其提出了改進的MULTIBAND-96，使它適合網絡協調控制的需要，并且算法可以在很大程度上優化模型的求解時間[5]。盧守峰等人在基本MAXBAND模型中加入了交通流離散Robertson模型的約束條件，解決了交通流離散造成的MAXBAND模型的局限性[6]。陳寧寧等人在傳統MAXBAND模型中引入動態紅燈排隊消散時間模型約束條件，建立了改進的MAXBAND模型，改進的MAXBAND模型與原模型相比較，實際有效綠波帶寬增加31.6%，車流主要行駛方向車輛平均延誤減少12.6%[7]。

雖然MULTIBAND模型比MAXBAND模型加入了交通流量和綠波速度等約束條件，更適合城市道路信號協調控制的要求，但由于MULTIBAND模型的綠波帶寬嚴格按照帶寬中心線對稱，這樣就會造成綠波帶寬的求解范圍小等問題。針對這一問題，張超和Gartner等人提出AM-Band模型的概念，通過對綠波帶寬對稱系數的改變，建立了一種不對稱多波段（AM-Band）模型，可以更好地利用每個方向上可用的綠燈時間，在AM-Band模型中，每個前進方向的綠波帶并不一定是關于中心對稱[2]。唐克雙等人提出一種非對稱綠波的概念，對基本MULTIBAND模型進行改進。綠波帶寬不一定是相對于綠波帶中心是對稱的，這樣的改進使干道綠波帶寬產生了不同的不對稱寬度，與多帶寬模型相比該模型提供了額外的靈活性，可以更好地利用每個前進方向的可用綠燈時間[8-9]。

綜上所述，現狀的大多綠波協調控制模型都是針對干線信號協調控制進行研究，這些模型對于非直線路徑適用度不高。本研究考慮如何將經典的城市干線協調控制模型進行改進，適應路徑協調控制的要求，滿足城市通勤交通的需求。為了使綠波協調模型適用于非直線的路徑，需要對現有的綠波控制模型的目標函數和不等式約束條件進行改進和修正。本研究中，基于經典的可變帶寬MULTIBAND綠波協調模型，目標函數方面加入了通行能力折減系數的影響考慮；對于約束條件，引入不對稱帶寬的概念對于帶寬約束條件進行改進，加入交通流離散模型對于綠波速度約束條件進行改進，進而建立了面向路徑的不對稱帶寬協調控制模型。

1 城市道路交通路徑特點分析

城市道路交叉口具有轉向、連接的功能，其中交叉口的轉向功能對于城市路徑的通過能力至關重要。交叉口轉向一般分為左轉、右轉和調頭三種形式。由這三種形式組成四種基本路徑類型：Z字型路徑、反Z字型路徑、U字型路徑和倒U字型路徑。經過右轉—直行—左轉的路徑因為形似大寫的英文字母Z，故定義為Z字型路徑。反Z字型路徑，與Z字型路徑相似，只不過其轉向順序為左轉—直行—右轉。此外，轉向順序為左轉—直行—左轉的路徑因形似大寫的英文字母U，故定義為U字型路徑，同理，經過右轉—直行—右轉的路徑定義為倒U字型路徑。在城市通勤交通中，車輛行駛的路徑往往是這四種路徑基本形式與直線型路徑的組合形式。

非直線型路徑信號協調控制與直線型路徑信號協調控制相比，有如下特點：（1）非直線型路徑由于要經過交叉口轉向，通過能力較直線型路徑有所降低，所以在同等交通流量的情況下，車輛通過時間變長，行駛速度降低，進行信號協調時的所需帶寬要較寬。（2）交通流在經過非直線路徑時的車隊離散度較直線型路徑更大，由于受交叉口轉向的影響，車輛行駛速度的變化范圍更大，車隊的穩定性更低。

由于非直線型路徑信號協調控制具有以上兩個特點，本文基于經典的MULTIBAND不對稱帶寬協調控制模型，充分考慮上述路徑信號協調的特點，加入了路徑離散模型對于綠波速度進行約束，同時在目標函數中亦加入了通行能力折減的影響。

2 面向路徑信號協調的MULTIBAND改進模型

2.1 不對稱帶寬的MULTIBAND改進模型

由于傳統的MULTIBAND模型的綠波帶嚴格按照綠波帶中心線對稱，這樣就會造成綠波帶的帶寬求解范圍小和綠波帶運行不穩定等問題。對于路徑信號協調由于轉向帶寬與直行帶寬不同，傳統的MULTIBAND模型關于綠波帶中心對稱就不合適。本文中一種不對稱帶寬的MULTIBAND改進模型。這個改進模型放寬了對于MULTIBAND模型關于綠波帶中心對稱的要求。

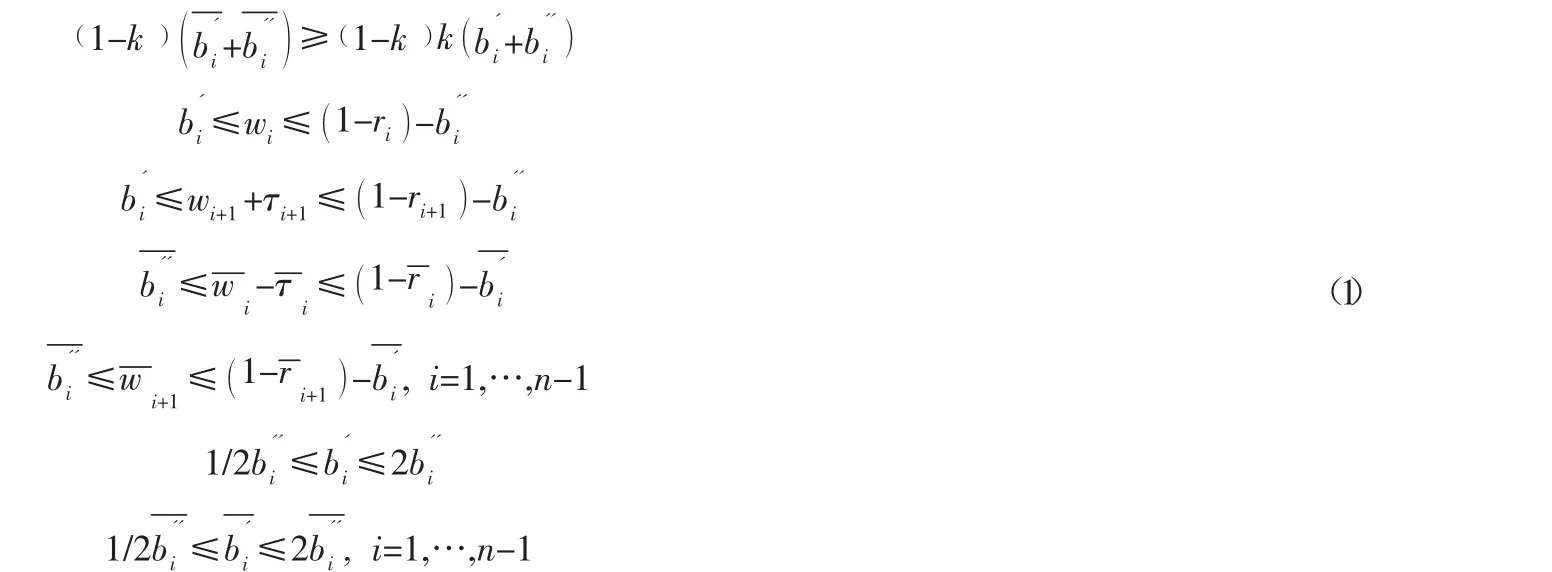
2.2 加入交通離散模型的改進MULTIBAND模型

在實際的交通狀況中，所有的車輛都假定它們的速度相同，并且在道路上沒有明顯變化。由于車輛性能和種類的不同，就會造成交通流的離散現象。這里用一種典型的交通流離散方法Robertson[10]方法。Robertson方法假設速度頻率變化符合幾何分布，模型如下：

式中：T是車輛行程時間（s）；λ是車輛行駛在路段之間平均行駛時間的80%；a是車隊離散系數；g（T）是時間概率密度分布函數。

圖1 不對稱帶寬MULTIBAND模型時距圖

在城市路徑中由于受到左轉、右轉的影響，城市路徑的離散程度與傳統的干線協調離散程度不同，本文加入離散模型的約束條件對于MULTIBAND模型進行改進。由于基本的MULTIBAND模型有約束條件：

式中：di為相鄰交叉口之間的距離（m）；fi為交叉口上行方向車速的最小值（m·s-1）；ei為交叉口上行方向車速的最大值（m·s-1）。

其中：fi和ei可以用計算公式：

式中：Tf是相鄰交叉口行程時間的最大值（s）；Te是相鄰交叉口之間行程時間的最小值（s）。

Tf和Te的具體值可以通過上面Robertson離散模型的公式[11]得到：

如圖2所示，例如選取97%的車流集中度，那么在公式中得到PP車流集中度的取值可以根據情況而定，可以根據高峰和平峰不同的交通情況對于車流集中度P進行取值，從而得到A和B不同的值對于模型進行約束。

根據以上的約束條件，加入交通流離散模型得到綠波速度的約束條件為：

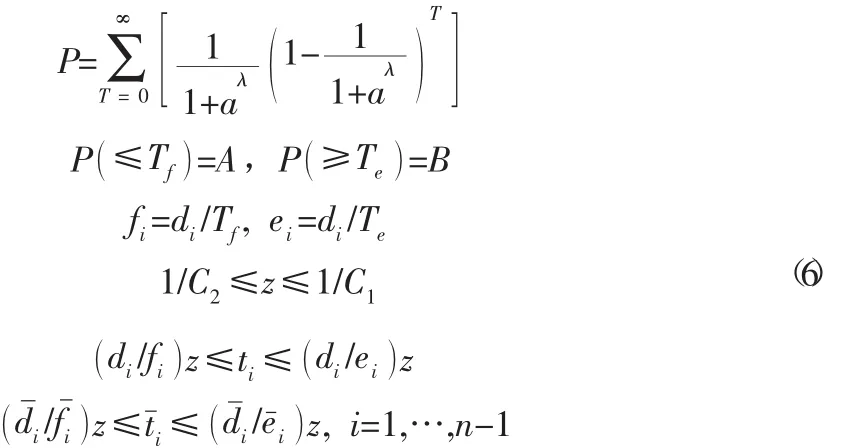
2.3 加入通行能力折減系數的改進MULTIBAND模型

2.3.1 三種通行能力模型

圖2 車流集中度時間—概率密度圖

（1）直行通行能力模型

直行車道飽和車頭時距可以利用平尾均值的方法得到。平尾均值也是總體均值的一種估計[12]。平尾均值就是將一列升序排列的數值，規定一個平尾的百分比，將異常的數值削減到與中間正常數值的平均值相等，將異常數值限制到一定的程度，最后將中間各樣本數值與首尾異常值的樣本平均值一起進行算數平均。對于直行車道的飽和車頭時距主要采用調查統計的方法得到。將直行開始放行的前5輛車予以剔除，并用平尾均值法處理數據得直行飽和車頭時距h為：

式中：h為飽和車頭時距平均值（s）；n為統計的車輛樣本量；hi為樣本量按照升序排列的飽和車頭時距 (s)；α為平尾百分比。

通過上述公式可以得到直行飽和車頭時距進而得到直行通行能力模型：

式中：h為直行飽和車頭時距 (s)；gi為直行相位的綠燈時間 (s)；T為交叉口周期時長 (s)。

（2）左轉通行能力模型

根據城市道路的具體情況，可以把交叉口左轉通行能力模型分為以下三種。

①拓寬專用左轉車道通行能力模型

左轉平均飽和車頭時距也可以通過平尾均值法進行計算。通過上述公式（7）可以得到左轉飽和車頭時距平均值，進而可以得到左轉專用車道的通行能力模型[13]為：

式中：CL1為左轉專用車道通行能力（pcu·h-1）；tg為左轉綠燈時間（s）；vL為左轉車流的速度（m·s-1）；a為平均啟動加速度（m·s-2）；T為信號周期時長（s）；hz為左轉平均飽和車頭時距（s）。

②設有左轉待行區的左轉車道通行能力模型

設有左轉待行區的左轉車道通行能力模型[13]為：

式中：C為左轉車道的通行能力（pcu·h-）1；T為信號周期時長（s）；n為一個信號周期內左轉待行區內原有的車輛數；t

L2p

為左轉綠燈時間與黃燈時間之和（s）；ts為左轉車輛的啟動時間（s）；為左轉車輛駕駛員的反應時間（s）；th為左轉飽和車頭時距均值（s）。

③允許掉頭的左轉車道通行能力模型

允許掉頭的左轉車道通行能力模型[14]為：

式中：hm為混合車流的平均車頭時距（s）；hL為左轉車流的平均車頭時距（s）；hU為掉頭車流的平均車頭時距（s）；PL為左轉車流的比例；PU為掉頭車流的比例；tgi為有效綠燈時間（s）；T為信號周期時長（s）；CL3為允許掉頭的左轉車道通行能力（pcu·h-1）。

（3）右轉通行能力模型

右轉交通要考慮行人和非機動車對于右轉交通的影響，由于中國人過馬路喜歡組隊一起通行，可以把行人和非機動車隊伍看成人群和非機動車群用可穿插間隙理論計算受影響時右轉交通的通行能力[15]。得到交叉口右轉通行能力的模型為：

式中：ht為右轉車輛車頭時距（s）；tgx為每周期內的右轉車輛不受行人和非機動車影響的時間（s）；T為信號周期時長（s）；Gc為綠燈時間內行人群的數量；tc為右轉車輛所能穿越行人群的臨界間隙時間（s）；tf為右轉機動車的隨車時距（s）；λ為行人群的單位時間數，λ=Gc/3 600；Gb為綠燈時間內非機動車組群的數量；te為右轉車輛所能穿越非機動車組群的臨界間隙時間（s）；η為非機動車組單位時間的到達率。

2.3.2 通行能力折減系數

本文通過增加一個在交叉口轉向折減系數對于綠波帶寬進行折減，從而體現城市路徑的特點。本文用交叉口轉向通行能力（包括左轉與右轉）與交叉口直行通行能力的比值定義折減系數。由于城市交叉口情況復雜，對于不同的交叉口情況要利用不同的折減系數進行折減，不同的城市行駛路徑折減系數也不同。本文結合上面的交叉口轉向通行能力模型對于折減系數βj進行分類折減，具體折減公式如下所示：

式中：βj為交叉口轉向折減系數；Cz為交叉口轉向通行能力（pcu·h-1）（包括直行左轉與右轉，具體根據路徑情況而定）；C為交叉口直行基本通行能力（pcu·h-1）；β1為直行時的折減系數；β2為拓寬專用左轉車道時的折減系數；β3為設有左轉待行區的左轉車道時的折減系數；β4為允許掉頭的左轉車道時的折減系數；β5為右轉時的折減系數。式中其它符號的含義同2.3.1節。

由于通行能力的折減系數都是小于等于100%，通行能力的折減系數與綠波帶寬應成反比的關系，根據這個關系，對于改進MULTIBAND模型的目標函數進行更改，重新得到的目標函數為：

2.4 改進后的MULTIBAND模型

通過以上三種方法對于基本MULTIBAND模型目標函數以及約束條件進行改進，得到了面向路徑信號協調的新模型為：

3 案例仿真與分析

以江蘇省常州市天寧區晉陵中路—關河中路—和平北路組成的Z字型路徑為例，對上述模型進行仿真驗證，該路徑包括飛龍東路—晉陵中路、晉陵中路—關河中路、關河中路—永寧路、關河中路—和平北路、和平北路—博愛路5個交叉口，該路徑是連接聚博花園等居民小區和江蘇省常州高級中學等學校的一條主要路徑，高峰時刻上下學的通勤OD交通需求較大。

根據調查流量和飽和流率等情況，本文首先利用Webster法[16]對于各交叉口單獨進行信號配時，求得周期最大的交叉口為關河中路—和平北路交叉口，周期為140s，進而將其作為信號協調控制的關鍵交叉口，其他交叉口周期也相應的調整至140s。

利用混合整數規劃求解軟件LINGO對2.4節的模型進行求解，周期約束本文取130～150s，速度約束取28.8～43.2km/h，相鄰交叉口路段間的速度變化范圍是7.2km/h，排隊消散時間參數τi，這里設為10s[7]。根據以上約束條件，求解出bi、wi、ti等參數，進而計算出相鄰交叉口間相位差[8]。

根據調查數據在交通仿真軟件VISSIM中建立仿真路網，根據上述相位差生成協調控制方案，通過仿真運行結果對路徑控制效果進行整體評價分析。將本文模型與Synchro軟件仿真結果，及MULTIBAND模型的結果進行對比，如表1所示。從中可以看出，相對與Synchro優化模型結果，本研究的模型在整條路徑上延誤時間和停車次數分別減少了9.2%和19.3%，路徑上車輛的平均行駛速度增加了17.2%，整條路徑的每小時通過能力增加了14.4%；相對于MULTIBAND模型優化結果，本研究的模型在整條路徑上延誤時間和停車次數分別減少了3.9%和9.7%，路徑上車輛的平均行駛速度增加了7.5%，整條路徑的每小時通過能力增加了8.1%。

表1 各協調控制方案的路徑仿真評價對比

4 結束語

通過加入路徑通行能力折減系數對于傳統MULTIBAND模型的目標函數進行改進，體現路徑信號協調的特點，進而引入不對稱帶寬的概念對于帶寬約束條件進行改進，在此基礎上加入交通流離散模型的考慮，對于路徑綠波速度約束條件進行改進，建立了面向路徑的不對稱帶寬協調控制模型。相關的案例分析顯示，與傳統Synchro模型相比，在延誤、停車次數、路徑通過能力等方面的改善在10%～20%之間，效果顯著；與經典的MULTIBAND模型相比，在停車次數、路徑通過能力等關鍵指標上，亦有接近10%的改善，表明該模型更加適合路徑協調的需求。

本研究提出的模型中雖然存在排隊消散時間參數τi，但是τi需事先給定，對其能否保證與模型計算的結果保持一致，是不是符合實際協調的情況，需要進一步深入研究。此外，研究的案例為基本Z字型路徑，模型對于其它基本路徑模型適用性實際驗證，有待進一步研究。