“一元二次方程”(第一課時)單元教學設計
江蘇省啟東市東安中學 陸佩佩
一、教學背景
為了進一步提升“自學·議論·引導”教學法試驗區初中數學骨干教師的業務水平和教學能力,提高教育教學質量,促進教師專業發展,于2017年11月在江蘇南通啟東開發區中學舉辦了“自學·議論·引導”教學法第三期專題培訓活動,同時開展了單元教學設計比賽,課題“一元二次方程”(第一課時),本文呈現該課題的教學設計,并對其設計意圖,進行了闡述,不當之處,敬請指正。
二、教學目標
1.通過類比探究的方法,知道一元二次方程的概念。
2.掌握解一元二次方程的基本思想和具體方法。
3.初步經歷解一元二次方程的四種方法,體會轉化的數學思想。
三、教學過程
類比思考,認識一元二次方程。
給出下列方程,指出相同點和不同點。
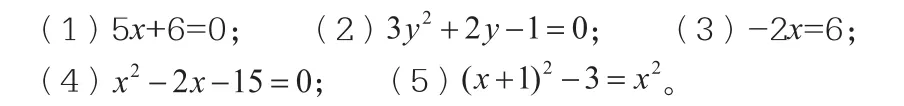
相同點:都含有一個未知數,都是整式方程。
不同點:未知數的次數不同,有的是1,有的是2。
問題1:哪些是學過的?能否給沒學過的方程取個名字?
生:已學過一元一次方程,一元二次方程。
由學生仿照一元一次方程的概念來給一元二次方程下定義。
【設計意圖】學生在小學已學習了方程,在七年級又知道了一元一次方程,所以對方程有一定的認識,故沒有用情境問題引入,而是開門見山用類比的數學思想引入一元二次方程,指明這節課學習的內容。
問題2:回憶一元一次方程的一般形式,你能否說出一元二次方程的一般形式?
生:一元一次方程的一般形式是ax+b=0(a≠0),一元二次方程的一般形式:(a≠0)。
師生共同活動:知道一元二次方程的有關概念:二次項,二次項系數,一次項,一次項系數,常數項。
鞏固練習:把下列方程化成一般形式,并指出二次項及系數,一次項及系數,常數項。

【設計意圖】一元二次方程中的概念比較多、雜,學生在后面的解方程中常搞錯,所以讓學生通過動手練習,能理性地掌握了一元二次方程的一般形式以及各個概念,為后面學習解方程打下扎實的基礎。
問題3:在學完了一元一次方程的概念后,該學哪些內容呢?
生:解方程和實際應用
師:說得太好了。那么如何解一元二次方程呢?
師:你的理論根據是什么?
生:平方根的意義。
師:這個方法稱為“直接開方法”。還有其他方法嗎?
【設計意圖】對于利用平方根的意義來解方程,學生能很快接受。如果把方程稍作變形,使方程右邊等于0,左邊正好可以因式分解,把二次降為一次,轉化為一元一次方程來解。此時學生遇到了思維上的障礙,激發起學生的求知欲。
生:方程的左邊可以因式分解,化成兩個一次因式的乘積。
師:說得很棒,如果方程的一邊等于0 ,另一邊能化成兩個一次因式的乘積,從而解出方程,這種方法稱為“因式分解法”。
【設計意圖】這兩個題看上去形式不同,但其實質是相同的,學生會覺得既熟悉又陌生,這會引起學生的探索欲望,想進一步知道這兩個題的解法。從而積極思考,促進學生思維能力的提高。
得出結論:方程2可通過適當的變形和方程1相同,所以又學會了配方法。
學生發現方程有解的時候,它的解與系數a,b,c有關。
師:方程第四種解法就是“公式法”。
【設計意圖】
教師引導學生概括,總結:(1)解方程的基本思想:降次,轉化為一元一次方程。(2)一元二次方程的解法有:直接開方法,配方法,公式法,因式分解法。具體方法的鞏固可在后面的學習中完成。
四、設計說明
平時的常規教學有時對學生的思維發展,能力探索等方面的提升并不顯著,單元教學的教學設計卻像注入了一股清泉,讓教師和學生的教和學有了新的活力,自從參加了全國有名的教育專家李庾南老師的教學培訓后,對自己的教學作了很多的改變,受益匪淺。這節一元二次方程的教學就采用了單元教學法。首先給出幾個不同類型的方程,讓學生去判別,由于學生已經學過了一元一次方程的概念及一般形式,所以一元二次方程的引入很直接,學生能遷移,自主獲得新知,對于一元二次方程的四種解法,都有著一定的聯系,且相互之間又可以轉化,所以教師幫助學生建立知識體系框架,即形成“整體”知識,為后面的課打下扎實的基礎。那么如何有效地讓學生了解這四種解法呢?根據平方根的意義給出直接開平方法,再從直接開平方法,可以通過適當的變形自然過渡到因式分解的方法。接著給出兩個方程讓學生明白方程還可以通過配方可轉化為熟悉的方法去解決。所以方程的一般形式在有解的情況下也可以配方,進而發現方程的解與系數有關,得出方程的另一種解法“公式法”,這樣把這四種方法自然地結合在一起,不僅讓學生明白解方程的方法,而且知道一個方程可能有幾種解法。這樣的單元教學,有利于學生把握知識的生成過程,知識的本質,知識間的相互聯系,也培養了學生自我探索,體驗的學習主體性。

