初中數學教學中數形結合思想的應用

陳宜建

(福建省三明市第三中學 365000)

一、在教學中培養學生數形結合的意識

數形結合思想在初中數學的運用中是非常廣泛的,數形結合顧名思義是指將繁瑣復雜的數字與直觀立體的圖形結合起來,并通過一定的轉換,解決問題.我國數學家華羅庚說:“數形結合百般好,隔離分家萬事非.”有了數形結合思想的幫助,對于解答初中數學問題有很大的幫助.老師幫助學生建立數形結合的思維方式,有利于學生更好地解決問題,認清數學的實質,有利于教學質量的提高.在初中教學中,培養學生建立數形結合思想意識是非常重要的.那么如何培養學生的數形結合思維,并將它們運用到實際問題中呢?

正所謂“興趣是最好的老師”.要討論如何在教學中教會學生運用數形結合思想去解決問題，首先要解決如何培養學生的數形結合思想,以及如何激發學生的興趣.得益于當前社會經濟與科學技術的發展，多媒體等電子教學設備已經走進了學生們的教學課堂中.運用多媒體設備，老師對學生進行數形結合思想的培養無疑會簡單許多.例如初中數學中有一類計算兩車相遇的問題，在講解這類題目時，教師不妨先運用多媒體將兩車相遇問題轉換成兩直線之間的距離問題，將題目更加簡單明了地呈現出來，再引導學生運用數學方法得出答案.此外,在數學問題中,老師要引導學生多多實踐,鼓勵學生將數形結合思維運用到實際問題中.

二、數形結合思想在初中數學有理數中的應用

有理數章節在初中數學中是重點教學內容.有理數這一章節的學習是實數,代數式,不等式方程學習的基礎,由于有理數是整數和分數的集合,教師在開展這一章節的學習時，可有效地利用數軸來表示任意有理數，同時這也是數形結合思想中典型的實例應用.例如，若a>0，b<0，且∣a∣>∣b∣，比較a，b，-a，-b之間的大小關系.這道題要比較他們之間的大小關系,就需要畫出數軸來進行明確的表述,絕對值在這里指的是在數軸上這個數的點到原點的距離,畫出數軸,從而得出這四者之間的大小關系.如果只是用具體的數如設a=4,b=-3,這種特殊值法雖可解出結果，但不免留下以偏概全的嫌疑.這種畫數軸的方式,不僅簡單易懂,還會使得解決問題的方法更具有全面性而且準確率大大提高.

三、數形結合思想在初中數學代數中的應用

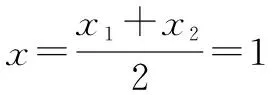
四、數形結合思想在初中數學概率計算中的應用

概率是初中數學教學的重點內容之一，概率的學習與現實生活也有著極其緊密的聯系.但因為這部分內容具有一定的抽象性，往往老師在教學過程中存在一定的講解困難，學生在學習過程中也會產生理解上的困難.因此，針對于概率章節的教學，我們在教學過程中引入了數形結合的方法，將其運用到概率的學習中，可以使復雜的問題簡單化，原本抽象的問題變得具體，從而輕松地解決問題.例如，概率中有部分幾何概型的運算，就是典型的運用數形結合思想來解決問題.通過計算圖形的面積，用圖形的面積之比來表示最終結果.

五、數形結合思想在幾何題中的應用

初中數學除了代數數字部分的運算外,另外一大塊重點就在于幾何問題的處理.有的學生空間思維能力不強,不能將幾何圖形有效地結合起來,導致這一塊處理起來十分的復雜.對于這種情況,老師應在數學的教學過程中積極地鼓勵學生,引導學生,多嘗試著去用數形結合的方法去解決一些圖形問題..

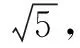
由上面例子可以看出,要靈活地運用數形結合的思想方法,由空間向數字,由數字向空間,相互轉換,老師可在日常的教學活動中逐步地向學生滲透,讓學生多多運用這種方法解決問題,使得學生逐步建立起知識體系,學會靈活地處理數學問題,建立起自己的數學思維.

隨著新課改的不斷深化，初中數學教學也在隨之發生變化，傳統的教學模式在逐漸被改變，取而代之的是教師利用現代化設備進行的更為多元化的教學模式.數學是一門以研究客觀世界的數量與空間幾何之間的關系的學科，它同時具有數字的邏輯性、嚴密性，和幾何圖形的直觀性，因此，數學學科具有一定程度上的復雜性，數學學科的學習也有一定的困難性.而數形結合思想作為一種重要的數學學習手段，在學生學習數學的過程中具有連接數字和空間幾何圖形的作用，能夠將復雜抽象的數據轉化成直觀易懂的幾何圖形，大大降低了學生學習數學的難度.