數列與其他知識交匯命題思路再探

☉江蘇省鎮江中學 王 磊

近幾年高考數學命題特點是注重知識的交匯點和結合點，以及數學知識之間的縱向和橫向的有機聯系.數列是考查同學們邏輯思維能力和推理能力的好素材，新課標下的高考對數列的考查呈現出綜合性強、立意新、難度大的特點，注重在知識交匯點設計問題，考題往“桃李嫁接”的方向發展.下面舉例剖析，供參考.

一、數列與推理的交匯

歸納推理是高中數學的重要內容，也是學習高等數學的基礎和重要工具.近幾年高考加大了對推理與證明的考查力度，而利用歸納推理解決數列問題成為高考的一個新亮點.

例1 在日本東京舉行的第52屆世乒賽期間，某商店櫥窗里用同樣的乒乓球堆成若干堆“正三棱錐”形的展品，其中第1堆只有1層，就一個球；第2，3，4，…堆最底層（第一層）分別按圖1所示方式固定擺放，從第二層開始，每層的小球自然壘放在下一層之上，第n堆第n層就放一個乒乓球，以f（n）表示第n堆的乒乓球總數，則f（3）=______；f（n）=______（答案用n表示）.

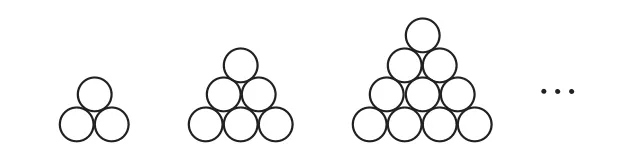
圖1

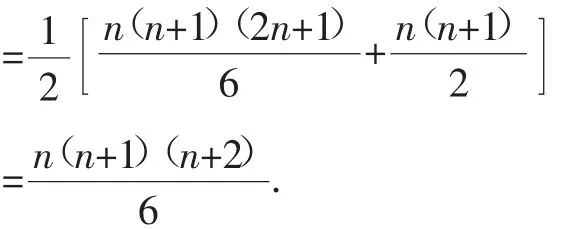
歸納推理是通過對特殊的、具體事物的分析、認識、研究，從而導出一般性結論的方法.在歸納推理中，根據同一個前提，有時可以得出不同的結論，這種結論的正確性有時是很難證明的，而且由幾個特殊對象歸納出的結論也不一定正確，還要經過邏輯證明和實踐檢驗.

二、數列與算法的交匯

例2 執行如圖2所示，的程序框圖，若p=0.8，則輸出的n=______.

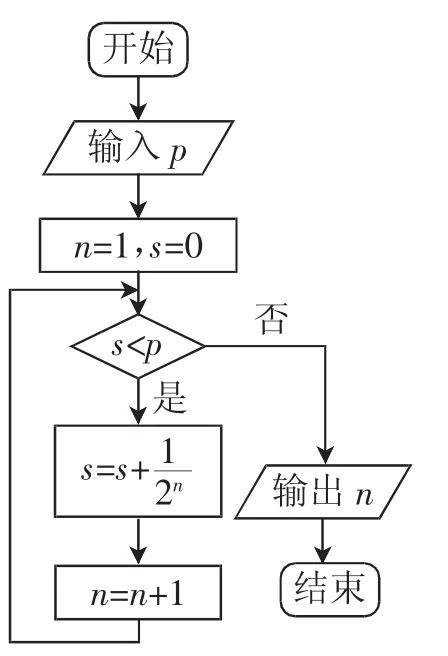
圖2

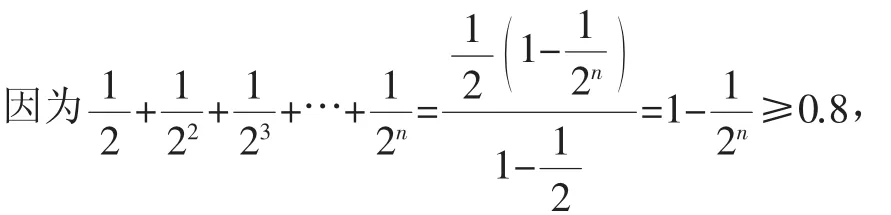
數列與算法的結合考查是高考的一個新“靚點”，在各個省的自主命題中都有體現，同學們在學習時要注意對其規律進行總結，熟練轉化為數列問題進行處理.變量追蹤法解決問題思路簡單，但往往過程煩瑣，而且步驟太多時不易操作，但將此題轉化為數列求和問題與解不等式問題，就使得解題的藝術性和思想性大大提高.

三、數列與三角的交匯

（1）求數列{an}的通項公式；

（2）設bn=2nan，數列{bn}的前n項和為Tn，求Tn的表達式.

所以Tn=π［（2n-3）·2n+3］.

三角是高中數學中的一個重要內容，也是歷年高考的必考知識點，它與數列相結合進行考查的題目類型主要有下面四種：①角A，B，C成等差數列型；②角A，B，C成等比數列型；③三邊a，b，c成等差數列型；④三邊a，b，c成等比數列型.

四、數列與應用問題交匯

例4 第二屆夏季青年奧林匹克運動會于2014年8月16日～28日在江蘇南京舉行，從社會效益和經濟效益出發，某宣傳部門決定建立一個“科技展覽基地”，并以此發展旅游產業.根據規劃，本年度投入800萬元，以后每年投入將比上年減少倍.本年度旅游基地旅游業收入估計為400萬元，由于該項建設對旅游業的促進作用，預計今后的旅游業收入每年會比上年增加倍.

（1）設n年內（本年度為第一年）總投入為an萬元，旅游業總收入為bn萬元.寫出an，bn的表達式；

（2）至少經過幾年，旅游業的總收入才能超過總投入？

解析：（1）第1年投入為800萬元，第2年投入為800×

所以，n年內的總投入為

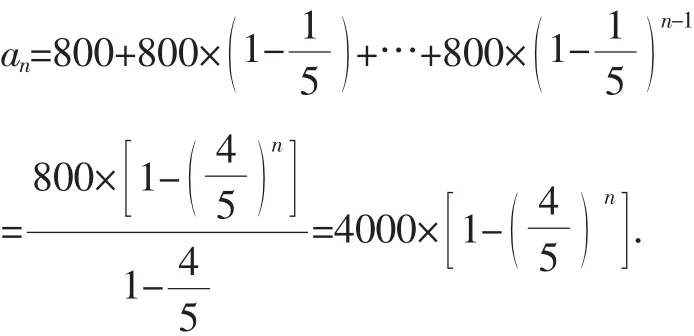
所以需要至少經過5年旅游總收入才能超過總投入.

投資理財中這一類問題通常可歸結為等比數列問題，利用等比數列知識求解，但往往要結合函數及不等式知識，對綜合能力要求較高.本小題主要考查建立函數關系式、數列求和、不等式基礎知識；考查綜合運用數學知識解決實際問題的能力.H