基于高考閱卷視角的解答題策略得分法*
☉內江師范學院數(shù)學與信息科學學院 劉成龍
☉四川省瀘州市瀘州高級中學 呂榮春
解答題是高考的重要題型,在整張試卷中占有較大的比重.如何在高考解答題的作答中取得較高的分數(shù)是一線老師們長期關注的焦點.為了解決這一問題,我們先了解一下評分細則的制定原則和呈現(xiàn)形式:基于數(shù)學本身、體現(xiàn)人文關懷,以采分點的形式呈現(xiàn).因此,一份試卷呈現(xiàn)的采分點越多,分數(shù)就越高.為了獲得較高的分數(shù),意味著要呈現(xiàn)出更多的采分點,尤其是在不能完全解答或不能解答的試題上多答出采分點.結合多年的高考閱卷經(jīng)歷,研究者認為策略得當,考生可以答出更多的采分點.基于此,研究者提出策略得分法.所謂策略得分法是指通過調整答題策略,使原先不能得分或得分較低的試題獲得更高分數(shù)的方法.常見策略得分的方法有七種:跳問得分法、缺步得分法、退步得分法、翻譯得分法、套路得分法、猜測得分法、高等工具得分法.下面對這七種策略得分法舉例說明.
策略一、跳問得分法
所謂跳問得分法是指跳過某一小問直接解答后面問題實現(xiàn)得分的解題方法.值得注意的是,對于一些遞進式設問來講,試題的每個問之間相對獨立,前一問無法解答并不影響后面問題解答,并且前一問待求或需證的結論往往可以作為解答后面問題的條件.
例1 (2018年全國卷Ⅲ理科第19題)如圖1,邊長為2的正方形ABCD所在的平面與半圓弧C(D所在平面垂直,M是上異于C,D的點.
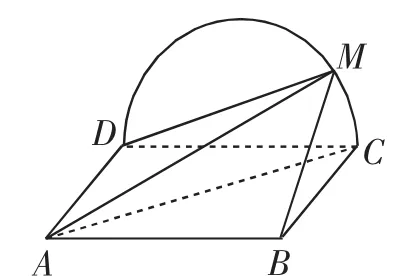
圖1
(Ⅰ)證明:平面ACD⊥平面ABC;
(Ⅱ)當三棱錐M-ABC的體積最大時,求面MAB與面MCD所成二面角的正弦值.
評析:本例第(Ⅰ)問與第(Ⅱ)問屬于獨立設問,即第(Ⅰ)問是否能夠解答并不影響第(Ⅱ)問的解答.因此,不能解答第(Ⅰ)問的考生可以直接解答第(Ⅱ)問.
策略二、缺步得分法
所謂缺步得分法是指解答問題時缺少某一步驟而給出其余步驟實現(xiàn)得分的解題方法.在解決問題時,可能某一步確實不能解答,但應跳過這一步繼續(xù)完成剩余步驟的作答,特別指出,為了表達的邏輯性,不能完成的這一步往往要囫圇吞棗式地冠以“易證”“化簡可得”等詞語.一般來講,根據(jù)高考閱卷評分細則,缺少步驟所對應的采分點不得分,但步驟之后呈現(xiàn)的采分點往往會酌情給分.
例2(2016年四川卷理科21題)設函數(shù)f(x)=ax2-alnx,其中a∈R.
(Ⅰ)討論f(x)的單調性;
評析:為便于說明缺步得分法,里先給出(Ⅱ)的參考答案[1]:

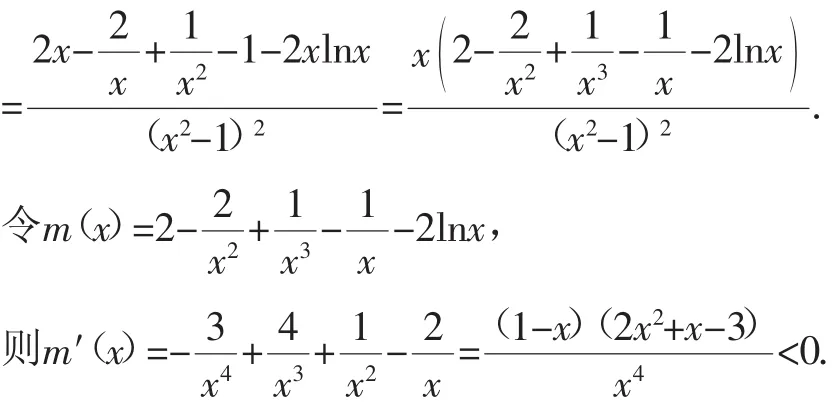
所以當x>1時,m(x)為減函數(shù),于是m(x) 從而h′(x)<0,于是h(x)在(1,+∞)上單調遞減. 在本例的解答中,m(x)的單調性證明具有較高的難度,對應的分值為4分.若未證明m(x)為單調遞減函數(shù)扣4分,但此過程后呈現(xiàn)的得分點均給分. 所謂退步得分法是指試題要求(或證明)一般情形下的結果(或結論),解答者退回到特殊情形作答實現(xiàn)得分的解題方法.對于某些試題解答受阻時,可以考慮研究問題的特殊情形,特殊情形不僅可以啟迪考生解答思路,往往也是高考閱卷的采分點. (Ⅰ)略; (Ⅱ)設O為坐標原點,證明:∠OMA=∠OMB. 評析:解答本例可以先研究最特殊的情形:①當l與x軸重合時,∠OMA=∠OMB=0°;②當l與x軸垂直時,OM為AB的垂直平分線,故∠OMA=∠OMB.事實上,特殊情形剛好是得分點. 例4(2017年全國卷Ⅰ理科第21題)已知函數(shù)f(x)=ae2x+(a-2)ex-x. (Ⅰ)討論f(x)的單調性; (Ⅱ)若f(x)有兩個零點,求a的取值范圍. 評析:解答第(Ⅰ)問時需要對a的取值范圍分類討論,如何確定分類的標準呢?不妨退回到a=0的情形,此時有f′(x)=-2ex-1<0,進一步觀察發(fā)現(xiàn)a<0時,f′(x)<0顯然成立,于是a≤0時,f(x)單調遞減.事實上,“當a≤0時,f(x)單調遞減”正是一采分點.第(Ⅱ)問求a的取值范圍,同樣可以運用退步得分法得分:當a≤0時,f(x)為單減函數(shù),故至多有一個零點. 所謂翻譯得分法是指將試題已知條件等價表征或將待求目標、待證的結論等價敘述實現(xiàn)得分的解題方法.解答中,當考生缺乏應對思路時,最為直接的得分策略是翻譯.翻譯分為兩部分:(1)直譯:將試題的條件或將待求目標、待證的結論用等價的方式表述;(2)延譯:將已知條件能推出的所有結論呈現(xiàn)在試卷中. (Ⅰ)求a,b的值. (Ⅱ)C上是否存在點P,使得當l繞F轉到某一位置時,有O—→P=O—→A+O—→B成立?若存在,求出所有點P的坐標與l的方程;若不存在,說明理由. 所謂套路得分法是指運用既定套路解答問題,從而獲得分數(shù)的解題方法.比如,解答直線和圓錐曲線問題的基本套路可概括為:設直線方程、聯(lián)立方程組、得到一元二次方程、運用韋達定理得兩根和與積、運用弦長公式計算等;再如,解答直線與圓錐曲線中點相關問題的基本套路為:設點、代點、找出中點表示方法等.事實上,在這些套路中往往隱含有采分點,會幫助我們意外得分. 例6(2018年全國卷Ⅲ理科第20題)已知斜率為k的直線l與橢圓為M(1,m)(m>0). (Ⅱ)略. 評析:本例(Ⅰ)涉及中點弦問題,解答的基本套路是:設點、代入橢圓、作差、變形等.具體步驟如下: 所謂猜測得分法是指根據(jù)數(shù)學條件合理地猜測一些數(shù)學結論實現(xiàn)問題部分解決,從而獲得分數(shù)的解題方法.猜想是對研究對象或問題進行感知、分析、聯(lián)想,在直覺的基礎上做出合乎一定經(jīng)驗與事實的判斷.猜想的常見方式有賦值猜想、經(jīng)驗猜想、結構猜想、類比猜想、直覺猜想、背景猜想等.盡管猜想僅能獲得問題的部分解,但絲毫不影響試題部分得分. 例7(2017年全國卷Ⅰ理科第17題)△ABC的內角A,B,C的對邊分別為a,b,c,已知△ABC的面積為 (Ⅰ)求sinBsinC; (Ⅱ)若6cosBcosC=1,a=3,求△ABC的周長. 評析:本例可以從多個視角進行猜測.(1)結構猜測:(Ⅰ)中求得sinBsinC,(Ⅱ)中已知cosBcosC,很自然猜測要運用公式cos(B+C)或cos(B-C).(2)經(jīng)驗猜測:面積為,經(jīng)驗告訴我們可知會用到面積公式;同時含有邊角關系,往往需要借助正弦定理統(tǒng)一成邊或角的關系;最后由cos(B+C)或cos(B-C)可以猜測要用到余弦定理.因此,答題中將公式cos(B+C)、cos(B-C)、面積公式、正弦定理、余弦定理全部呈現(xiàn)在答卷中必然會有一些得分點. 例8(2008年全國卷Ⅱ理科21題)設a∈R,函數(shù)f(x)=ax3-3x2. (Ⅰ)略; (Ⅱ)若函數(shù)g(x)=f(x)+f′(x),x∈[0,2],在x=0處取得最大值,求a的取值范圍. 評注:本例可以通過賦值猜想得分[2]: 易知g(x)=ax3-3x2+3ax2-6x=ax2(x+3)-3x(x+2).由g(x)在區(qū)間[0,2]上的最大值為g(0),于是當x=2時,有 所謂高等工具得分法是指運用高等數(shù)學中的工具解答試題,從而實現(xiàn)得分的方法.常見的高等工具有洛必達法則、Jensen不等式、泰勒展開式、拉格朗日中值定理、不動點理論等.高考閱卷并不排斥運用高等工具解答高考試題,只要有理有據(jù)即得分.因此,在歷年評分細則的制定中不乏運用高等工具解答的身影. 例9(2018全國卷Ⅲ理科21題)已知函數(shù)f(x)=(2+x+ax2)ln(1+x)-2x. (Ⅰ)若a=0,證明:當-1 (Ⅱ)若x=0是f(x)的極大值點,求a. 分析:本例含有深刻的高等數(shù)學背景,用初等解法涉及高難度的構造和煩瑣的運算,據(jù)閱卷場反饋信息來看,某省近30萬考生用初等解法完全做對的僅數(shù)人,但運用高等工具解答可以降低試題的難度,從而實現(xiàn)策略得分,如下: 文中介紹了策略得分法的常見七種類型,每一種類型并非獨立,這需要考生仔細品味.對于某一問題的解決可能運用多種策略,這需要考生在摸索中熟練掌握.總之,希望考生提高應考智慧,贏得更高的分數(shù),最終實現(xiàn)人生夢想.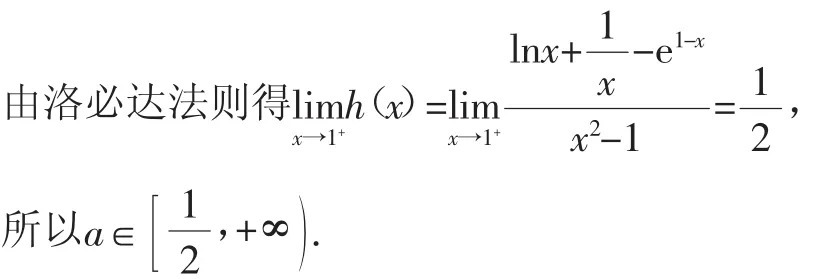
策略三、退步得分法
策略四、翻譯得分法
策略五、套路得分法
策略六、猜測得分法
策略七、高等工具得分法