基于Matlab平臺的圖論模型的仿真實驗

孫建英

(青島理工大學 琴島學院， 山東 青島 266106 )

圖論模型是數學建模中一類非常重要的模型，它的應用非常廣泛。購買機票、設備更新、配送路線選擇等，都屬于最短路徑問題；景區的旅游車輛的最大通行量、石油管道的最大輸送量等，都屬于最大流問題；電線的架設問題、居民區的供水管道問題等，都屬于最小支撐樹問題。Matlab2014a平臺中的圖論工具箱，可以實現圖論模型的快速求解，不必編寫復雜的程序，對計算機不是很懂的學者也可以很快地掌握。本文從3個實例出發，詳細介紹了如何利用圖論工具箱快速準確地求解圖論模型中的最短路、最大流和最小支撐樹問題，對圖論模型的進一步研究有重要意義和實用價值。

1 預備知識

1.1 圖論工具箱

Matlab2014a平臺下圖論工具箱中的相關函數，如表1所示。

表1 Matlab 圖論工具箱中的相關函數

1.2 稀疏矩陣

稀疏矩陣是指零元素很多，非零元素比較少的矩陣。

稀疏矩陣的存儲方式：a(i,j)=m，其中，a表示稀疏矩陣，i表示非零元素的行標，j表示非零元素的列標，m表示非零元素的數值。

稀疏矩陣的使用說明：1)有向圖中，可以直接使用Matlab中的sparse命令,把鄰接矩陣轉化為稀疏矩陣；2)無向圖中，由于Matlab只存儲下三角矩陣中的非零元素，要先把鄰接矩陣轉置，再應用sparse命令。

2 實例仿真

2.1 最短路問題

例1購買機票問題[1]：某集團公司在六個城市C1,C2,…,C6中有分公司，從Ci到Cj的直飛航程票價如表2所示(“-”表示無直飛航班)。如今，集團巡視組要分別從C1出發到其他城市去檢查工作。請問：應該如何安排航班，方可使得票價最低？

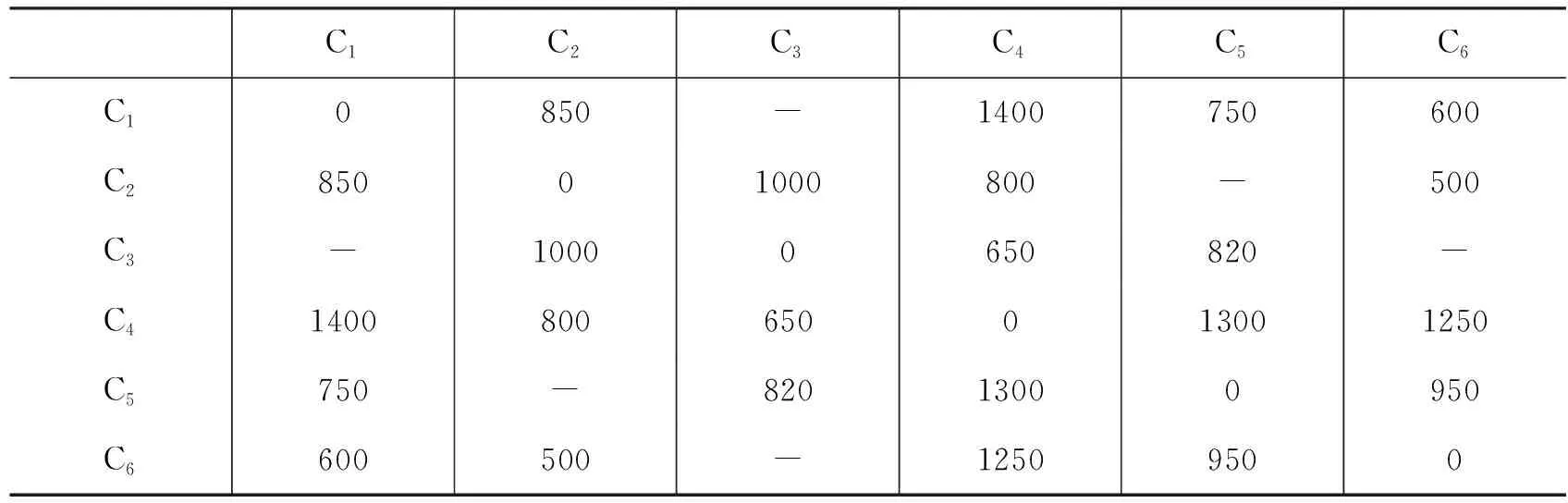
表2 各分公司所在城市之間的航程票價(單位：元)

解：Matlab程序：

clc,clear

a=zeros(6);

a(1,2)=850;a(1,4)=1400;a(1,5)=750;a(1,6)=600;

a(2,3)=1000;a(2,4)=800;a(2,6)=500;

a(3,4)=650;a(3,5)=820;

a(4,5)=1300;a(4,6)=1250;

a(5,6)=950;

a=a’;

a=sparse(a);

b=[1:6];

[price,path]=graphshortestpath(a,1,b,’Directed’,0)

運行結果：

price=

0 850 1570 1400 750 600

點擊工作區中的path，出現path變量表，見表3。

表3 path變量

結果分析：C1直達到C2，C4，C5，C6，票價分別為850，1400，750，600；C1經C5

轉機到C3，票價為750+820=1570。

2.2 最大流問題

例2管道輸流問題[1]： 某石油公司擁有一個管道輸送網絡系統，如圖1所示，使用該系統將石油從開采地A輸送到銷售地G。由于管道(以兩個地點之間的弧表示)直徑的變化，各段管道的容量是不一樣的，弧上的數字意味著各管道的最大容量(單位：萬加侖/小時)。請問：欲使得從開采地A到銷售地G每小時輸送的石油量最大，應采取什么樣的配送方案？最大配送量是多少萬加侖？

解：Matlab程序：

clc,clear

a=zeros(7);

a(1,2)=6;a(1,3)=8;a(2,4)=3;a(2,5)=6;

a(3,4)=4;a(3,6)=1;a(3,7)=3;

a(4,5)=3;

a(5,7)=5;a(6,7)=4;

b=sparse(a);

[Maxflow,path]=graphmaxflow(b,1,7);

Path=sparse(path);

Maxflow

view(biograph(Path,[],’ShowArrows’,’on’,’ShowWeights’,’on’))

運行結果：

Maxflow=9

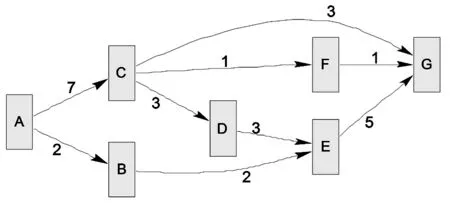
圖1 石油輸送量最大的配送方案

2.3 最小支撐樹問題

例3電線架設問題[2]：如圖2，S、A、B、C、D、E、T代表村鎮，它們間連線表明各村鎮間現有道路交通情況，連線旁數字代表道路的長度。現要求沿途中道路架設電線，使上述村鎮全部通上電，應如何架設使總的線路長度為最短？

解：Matlab程序：

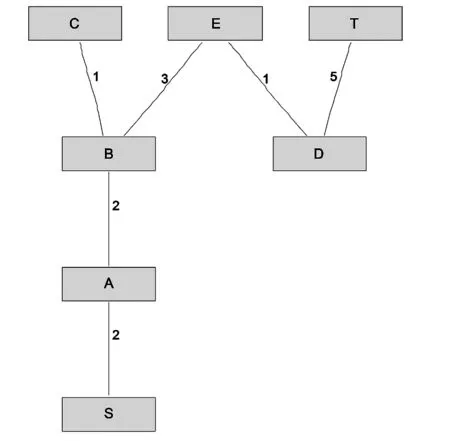
圖2 線路最短的電線架設方案

clc,clear

a=zeros(7);

a(1,2)=2;a(1,3)=5;a(1,4)=4;

a(2,3)=2;a(2,5)=7;

a(3,4)=1;a(3,5)=5;a(3,6)=3;

a(4,6)=4;

a(5,6)=1;a(5,7)=5;

a(6,7)=7;

a=a’;

a=sparse(a);

[ST,pred]=graphminspantree(a,’Method’,’Kruskal’);

st=full(ST);

treelength=sum(sum(st))

view(biograph(st,[],’ShowArrows’,’off’,’ShowWeights’,’on’))

運行結果：

treelength=14

3 結語

圖論中的最短路、最大流和最小支撐樹問題，在Matlab2014a平臺下，可以利用圖論工具箱快速地得到最優解。其實，運籌學中的很多模型，像整數線性規劃和目標規劃問題[3]等，也可以借助Matlab實現快速求解。但是還有很多問題，例如有初始可行流的最大流問題和最小費用最大流問題等，目前，Matlab沒有相應的函數可以直接求解，要轉化成線性規劃模型，再利用Matlab或者lingo軟件求解[4]。Matlab軟件已成為解決圖論問題的強有力的工具，可以幫助科研工作者及時、準確地作出決策。