六自由度機器人控制器參數(shù)的可區(qū)分性分析

魏雅慧 楊 超

(1. 三峽大學 大學生素質(zhì)教育中心， 湖北 宜昌 443002； 2. 三峽大學 電氣與新能源學院， 湖北 宜昌 443002)

六自由度機器人，即有6個關節(jié)節(jié)點，各關節(jié)由多軸運動控制器進行獨立地伺服控制[1]．閉環(huán)系統(tǒng)中的轉(zhuǎn)矩控制、速度控制及位置控制均由伺服控制器完成．為使閉環(huán)系統(tǒng)獲得較高的動態(tài)響應，需要優(yōu)化系統(tǒng)的驅(qū)動特性，即優(yōu)化控制器的參數(shù)，使機電系統(tǒng)達到最佳匹配，從而獲得最佳的穩(wěn)態(tài)和動態(tài)性能[2]．

由于六自由度機器人控制器的參數(shù)眾多，優(yōu)化目標和控制器參數(shù)之間的函數(shù)關系有時無法直接得到，難以用解析方法進行區(qū)分．因此，本文提出一種基于軌跡靈敏度的控制器參數(shù)可區(qū)分性方法，通過探討參數(shù)是否可被區(qū)分，判定參數(shù)優(yōu)化過程中是否存在唯一的最優(yōu)解．這種分析方法在電力系統(tǒng)動態(tài)分析中的應用比較成熟和廣泛．在電力系統(tǒng)穩(wěn)定分析研究方面，主要包括了能量函數(shù)法對穩(wěn)定裕度靈敏度進行計算[3]，網(wǎng)絡結構保持下的能量裕度靈敏度計算方法[4]，對單機能量函數(shù)下的軌跡靈敏度函數(shù)關系的推導，發(fā)現(xiàn)快速計算靈敏度和暫態(tài)穩(wěn)定極限的方法[5]．然而在控制系統(tǒng)中，基于軌跡靈敏度的分析方法應用較少，如介紹混合靈敏度控制在電液位置控制系統(tǒng)中的應用[6]，混合靈敏度控制方法在直驅(qū)式液壓系統(tǒng)中的應用[7]，電動助力轉(zhuǎn)向控制系統(tǒng)基于H∞的混合靈敏度算法[8]．

在實際應用中，包括結構參數(shù)及工作參數(shù)在內(nèi)的很多參數(shù)都能影響機器人系統(tǒng)的動態(tài)特性．靈敏度分析作為一種定量的分析方法，能有效地研究控制器參數(shù)對系統(tǒng)動態(tài)性能的影響[9-10]．本文通過分析靈敏度曲線的相位，確定不可區(qū)分的控制器參數(shù)，并以六自由度機器人單個模塊控制器為例進行分析，分析結果驗證了本文方法的有效性．

1 軌跡靈敏度的計算

軌跡靈敏度定義為當控制器參數(shù)發(fā)生一定變化時，相應的閉環(huán)系統(tǒng)動態(tài)軌跡的變化程度，反映了系統(tǒng)軌跡與控制器參數(shù)之間的關系．簡單地說，軌跡靈敏度是軌跡關于參數(shù)的導數(shù)，一般應用于非線性系統(tǒng)，且隨參數(shù)的變化而不同，具有時變性．狀態(tài)變量或輸出變量的軌跡變化對控制器參數(shù)的變化率，定義為軌跡靈敏度[11]

yi(K1，…，Kj，…，Km，t)]/ΔKj(1)

式中，yi為系統(tǒng)變量i的軌跡，Kj為系統(tǒng)參數(shù)，m為參數(shù)總數(shù)，t為時間采樣點．

為減小由式(1)帶來的誤差，提高計算精度，故采用中值法計算導數(shù)，即分兩次計算軌跡：

yi(K1，…，Kj+ΔKj，…，Km，t)

yi(K1，…，Kj-ΔKj，…，Km，t)

然后計算軌跡靈敏度的相對值：

yi(K1，…，Kj，…，Km，t)]/yi0}/(2ΔKj/Kj0) (2)

式中，Kj0為參數(shù)Kj的初始值，yi0為參數(shù)Kj0的穩(wěn)態(tài)值．

為了對各參數(shù)的靈敏度大小進行比較，對于軌跡靈敏度曲線上的各點，取其絕對值的平均值：

(3)

式中N為軌跡靈敏度曲線的總點數(shù)．

由此可得：若系統(tǒng)軌跡yi對參數(shù)Kj的靈敏度較大，則說明Kj對yi的影響較大，根據(jù)yi可以較容易地區(qū)分出Kj；反之，若所有的系統(tǒng)軌跡yi對參數(shù)Kj的靈敏度都非常小，則說明Kj對所有系統(tǒng)軌跡的影響微小甚至幾乎沒有影響，Kj不容易被區(qū)分．

2 從軌跡靈敏度的角度分析可區(qū)分性

在控制器參數(shù)的優(yōu)化整定過程中，該參數(shù)是否可被區(qū)分的判定標準為該參數(shù)能否被唯一確定．設模型中的兩個參數(shù)分別為Kj、Kj+1，分析系統(tǒng)軌跡可以發(fā)現(xiàn)，若Kj、Kj+1不可區(qū)分，則說明它們以一種隱函數(shù)的關系作用于軌跡[12]，即

y=f[K1，…，φ(Kj+Kj+1)，…，Kn，t] (4)

假設φ(Kj+Kj+1)對兩個參數(shù)均可導，根據(jù)微積分鏈式規(guī)則可得

(5)

則有

(6)

式中，?y/?Kj，?y/?Kj+1是時變的，而?φ/?Kj，?φ/?Kj+1是非時變的．因此，在時間軸上軌跡靈敏度?y/?Kj，?y/?Kj+1互相成比例即在零點處相交，若軌跡靈敏度是振蕩曲線，則表現(xiàn)為曲線同相位或反相位．

由上述分析可知，若一些參數(shù)的軌跡靈敏度曲線在零點處相交，則這些參數(shù)不能被唯一確定，即這幾個參數(shù)不能被區(qū)分．若所有參數(shù)的軌跡靈敏度曲線都不在零點處相交，那么所有參數(shù)基本上能被唯一確定．

3 單個機器人模塊的控制器模型

六自由度機器人的單個運動控制模塊相當于一個交流伺服系統(tǒng)，由位置回路、速度回路及電流回路3個反饋回路組成．性能要求如下：1)瞬態(tài)響應具有穩(wěn)定、平滑的特征；2)為獲得高精度的位置控制性能，系統(tǒng)需有較小的穩(wěn)態(tài)跟蹤誤差和動態(tài)位置跟蹤誤差[13]．該系統(tǒng)的控制模型如圖1所示．

圖1 交流伺服系統(tǒng)控制模型

本文采用的交流伺服系統(tǒng)為Ι型系統(tǒng)，對階躍輸入能無靜差地復現(xiàn)，但對于其他非階躍輸入，則要經(jīng)歷振蕩，為改善系統(tǒng)性能需要進行參數(shù)調(diào)節(jié)和附加控制環(huán)節(jié)．因此，將系統(tǒng)的伺服放大器、伺服電機及速度測量部分，整體作為伺服控制的調(diào)節(jié)對象對速度環(huán)進行簡化，簡化后的系統(tǒng)加入比例微分控制，最終得到的系統(tǒng)框圖如圖2所示．

圖2 加比例微分控制的交流伺服系統(tǒng)框圖

機器人模塊等效為一個二階系統(tǒng)，R(s)為輸入位置信號，P(s)為輸出位置信號，Kd、Kf分別為PID控制器微分、反饋比例系數(shù)．輸出位置信號：

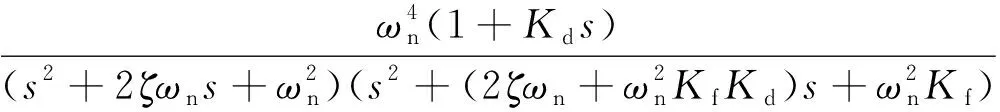
式中，ωn為伺服阻尼自然頻率，ζ為伺服阻尼比．

4 單個模塊控制器參數(shù)的可區(qū)分性分析

4.1 算例系統(tǒng)

如圖3所示，本文的研究對象為六自由度機器人位置控制系統(tǒng)，其型號為REBot-V-6R，定位精度±0.01 mm，作業(yè)半徑725 mm，S軸(回旋)動作范圍為±170°．該控制系統(tǒng)參數(shù)/輸入初值見表1．

圖3 六自由度機器人

參數(shù)/輸入ωnζKdKf初值0.2530.7202

以位置輸出P為軌跡變量，對應于式(1)中的y．由圖2可知，位置系統(tǒng)PID控制器包含2個參數(shù)Kd、Kf，對應于式(1)中的K．將這2個控制器參數(shù)在其缺省值的基礎上，上下變動10%，計算其軌跡靈敏度．表2為2個控制器參數(shù)對位置輸出P的軌跡靈敏度平均值．由表2可以看出，對于軌跡變量位置輸出P，Kf對其影響較大，Kd的影響較小．

表2 機器人控制器參數(shù)軌跡靈敏度

4.2 軌跡靈敏度與可區(qū)分性

以位置輸出P為軌跡變量，PID控制器參數(shù)Kd、Kf的軌跡靈敏度曲線如圖4所示．從圖中可以看出，以軌跡變量P為參考變量，參數(shù)Kd、Kf的靈敏度曲線在零點處相交，表現(xiàn)出同相位的特征，說明參數(shù)Kd、Kf不能被唯一確定，即它們是不可區(qū)分的參數(shù)．

圖4 PID控制器參數(shù)的軌跡靈敏度曲線

為了對上述結論完成進一步驗證，分別對Kd、Kf取不同的參數(shù)值，再對軌跡變量P進行Matlab仿真．本文對Kd、Kf的取值組合有3個，如下所示：

①Kd=20，Kf=2；

②Kd=7，Kf=9；

③Kd=6，Kf=8．

其中參數(shù)組合①為初值，而參數(shù)組合②，③為在使系統(tǒng)穩(wěn)定的參數(shù)區(qū)間內(nèi)任意選取的值．

仿真得到的軌跡動態(tài)曲線如圖5所示．可見參數(shù)組合②，③對應的動態(tài)軌跡相差不大，而與參數(shù)組合①對應的動態(tài)軌跡有較大區(qū)別，說明Kd、Kf為不可區(qū)分的參數(shù)，驗證了本文方法的有效性．

圖5 PID控制器參數(shù)軌跡變量仿真曲線

5 結 論

本文針對六自由度機器人系統(tǒng)，提出了控制器參數(shù)的可區(qū)分性問題，即參數(shù)的最優(yōu)解能否被唯一確定．提出了通過分析參數(shù)的軌跡靈敏度實現(xiàn)對控制器參數(shù)的可區(qū)分性的分析，為機器人控制系統(tǒng)參數(shù)的可區(qū)分性分析提供了新的途徑．研究結果表明，若一些參數(shù)的軌跡靈敏度曲線相交于零點，則說明它們之間存在相關性，為不可區(qū)分參數(shù)；若這些參數(shù)的軌跡靈敏度都沒有在零點處相交，也不存在線性相關的關系，則它們之間不存在相關性，為可以區(qū)分的參數(shù)．通過對具體算例進行分析，確定了參數(shù)Kd、Kf為該六自由度機器人單個模塊控制系統(tǒng)中，不能被區(qū)分的控制器參數(shù)，它們之間存在某種關系，在系統(tǒng)的優(yōu)化整定過程中無法被唯一確定．因此，為降低控制器優(yōu)化的維數(shù)、提高優(yōu)化效率，參數(shù)Kd、Kf可以取默認值，或者取經(jīng)過一次優(yōu)化整定后的值，不必再對其進行繼續(xù)優(yōu)化．