一道例題的有效變式練習
——min、max函數問題研究

張 琴

(河南省衡陽師范學院南岳學院 421000)

“問題是數學的心臟，如何高效的解決問題是數學的真諦”.筆者認為在講授“min 函數”時,可從一個簡單的min問題著手分散難點,通過例題的有效變式引領學生探究, 在解題過程中既能擴散學生思維，又能幫助學生提高解題能力．

一、數學中min、max函數有效變式案例分析

1.鋪墊式練習

定義符號min{p，q}含義為：當p≤q時，min{p,q}=p；當p>q時，min{p,q}=q.如：min{3,-1}=-1，min{-3，4}=-3.求min{2x,3}.

點評通過鋪墊式問題的探究老師引導學生思考，輔助理解,從而達到分散難點.

2.例題練習

求min{x2-1,-2}.

點評由前面的鋪墊很多學生自然想到要討論，但有些學生會發現不需討論.這時老師正好借此引導學生，即可將例題滲透到函數中,結合數形思想來分類討論問題,又能幫助學生快速地理解min函數圖象這個重難點.由此例題的轉化鋪墊,為后面的引導性問題滲透了數學思想的運用．

3.理解性變式練習

點評可將代數問題轉化為函數圖象問題來解決min函數，弄清min函數問題實質是在同一自變量時比較函數圖象的高低來解決．在此可順便提下最值，及函數增減性.

4.探究式變式練習

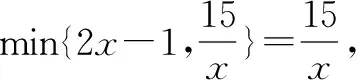
點評通過探究式變式練習的過程，老師引導學生去畫函數圖象，來解決實際問題.從而讓學生領會到借助函數的圖象，更突出了畫函數圖象解決min函數的問題的重要性 ，并且能全面地讓學生真正地認識min函數圖象的實質．

5.拓展化變式練習

(2)已知min{2x2-3x+n,-5}=-5，求實數n的取值范圍；

(3)已知當-1≤x≤2時，min{x2-2x-3，mx-m}=x2-2x-3, 求實數m的取值范圍．

點評通過近年來中考試題等新穎試題的要求 ，其實本質上要求學生以數形結合思想來解決函數問題,理解函數圖象是解決函數問題的根基．

6.類比變式練習

設xi(i=1,2,3,…,n)為任意代數式，我們規定：y=max{x1,x2,…,xn}表示x1,x2,…,xn中的最大值，如y=max{1，2}=2。

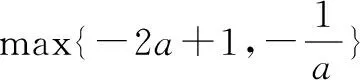
點評①類比變式練習可以高效地培養學生思維綜合，即實現數學學習中系統方法的掌握,又可以將相應知識之間有效地結合在一起，起到鞏固作用.

②類比思維可以高效地培養學生的數學解題、數學公式推導、擴展解題思維,同時也形成了對學生的數學思維以及邏輯思維等各方面能力的培養和創新思維的培養.

二、數學變式教學的實踐成效與反思

筆者認為在我們實踐數學變式教學中，教師可以精心設計數學中例題的有效變式的題目，題目可以步步深入地引導學生，并且讓學生從一系列題目“變化”的現象中發現問題始終“不變”的本質特征，又能讓學生從事物“不變”的現象中進一步探究事物“變”的現象和規律. 并將學生帶出題海戰術和應試教育，起到事半功倍.

1.變式教學是有效的，可提高學生的學習興趣，有利于數學知識的掌握，有利于學生能力的培養和思維水平的提升.

2.在變式教學中應在難度、數量和學生的參與度上有所把握，才可以使變式教學事半功倍.實踐證明，多進行變式教學，能幫助學生更加深刻地認識到該數學問題的本質特征.有利于培養學生的數學反思能力.

3.有效的數學變式能有效地幫助學生在面對同類型題時一看即有思路，不但為學生省下在遇到新題的重復精力及恐懼感，而且在老題型的思維發散上反倒鍛煉了學生數學思維.

筆者通過自己大量練習中考最值問題試題以及在教學方面的實踐中，總結出近年來中考試題等新穎試題的要求,其實本質上要求學生以數形結合思想來解決函數問題,理解函數圖象是解決函數問題的根基.因此筆者將min、max函數問題通過鋪墊式練習，引導學生將問題滲透到數學思想中，幫助學生輔助理解,分散難點.